【深度学习】卷积神经网络与 LeNet

在 softmax 回归中，我们使用的数据集是图像数据。这种数据的每个样本都是由一个二维像素网格组成，每个像素可能是一个或多个数值，取决于是黑白还是彩色图像。

我们之前的处理方式是通过“展平”，用一个标量表示一个像素，将图像数据展平成一维向量，这会导致图像空间结构信息的缺失，不够有效。

因为这些网络特征元素的顺序是不变的，因此最优的结果是利用先验知识，即利用相近像素之间的相互关联性，从图像数据中学习得到有效的模型。

下面要介绍的卷积神经网络就是一类强大的、为处理图像数据而设计的神经网络。

一、从全连接层到卷积

在之前的分类问题中，一张图片的形状是 28$\times$28，展平后输入维数变成 784，尚可以接受。

那如果输入的图片是百万级像素呢？这意味着模型的输入每次都有百万个维度。即使将隐层的维度设为 1000，这一全连接层的参数个数也有 $10^6\times10^3=10^9$ 个，想要训练这个模型将不可实现。

但是，目前的图像识别分类技术已经可以很好地处理越来越庞大的图像：这是因为图像中原本就存在着丰富的结构，且这些结构可以被人类和机器学习模型使用。

卷积神经网络(convolution neural networks, CNN)就是一种可以利用自然图像中的一些已知结构的创造性方法。

平移不变性与局部性

想象一下，假如我们想从一张图片中找出一个物体。一个合理的假设是：无论怎么找，能不能找到与这个物体所在的位置无关。

例如，猪通常不会在天上飞，但是，如果一只猪出现在图片顶部，我们还是能认出它。

下面我们借助一个儿童游戏“沃尔多在哪里”来说明。即在一张比较混乱的照片中，找到沃尔多。

沃尔多游戏示意图

尽管这个沃尔多能很好地融入周围的人群，在眼花缭乱的场景中找到他非常困难，但我们应该想到的是：不管这个这个沃尔多到底在哪，它的样子都是不变的。

因此，我们可以设计一个扫描检测器，它将图片分割成若干个区域，并为每个区域包含沃尔多的可能性打分。

平时在登录一些网站需要验证时，就出现过需要我们点击分成若干块的图像中关于“红灯”或者“高铁”等等的区域。

卷积神经网络正是将空间不变性(spatial invariance)的这一概念系统化，从而可以使用较少的参数来学习有用的表示。

此外，我们在寻找沃尔多时，通过只会关注我们的目光所及附近的区域，而不会过多关注其他较远的区域，这就是“局部性”原则。

综上，要想设计出适合用于计算机视觉的神经网络架构，就需要实现这两个特性：平移不变性(translation invariance)和局部性(locality)。

卷积核(convolutional kernel)或者称为滤波器(filter)，也可以简单称之为卷积层的权重，可以帮助我们实现。

其对输入矩阵做扫描运算（下图），可以得到一个维度更小的矩阵，从而减小模型所需参数的个数。

卷积过程

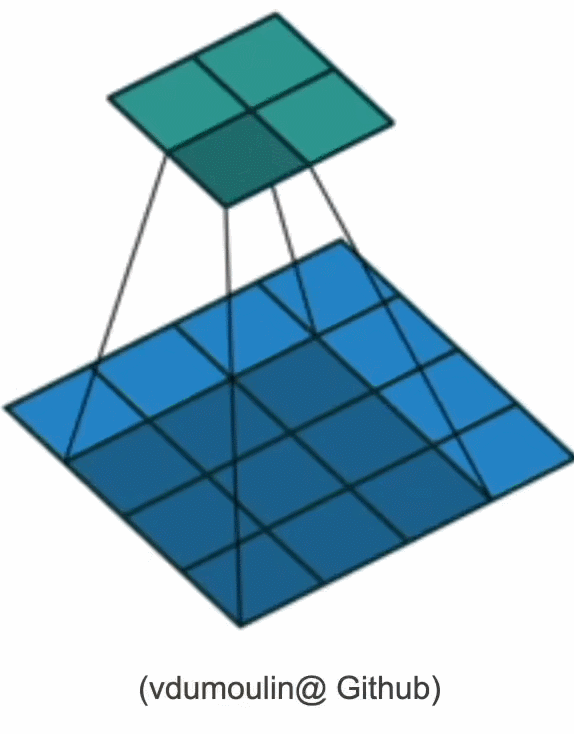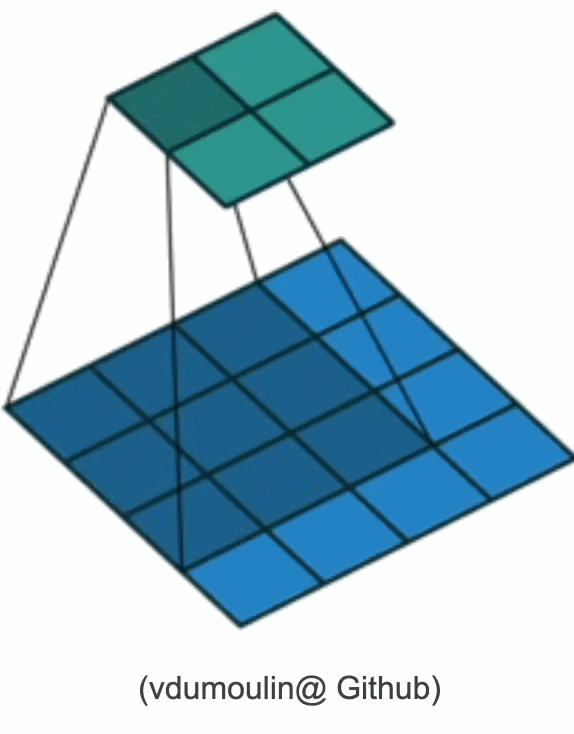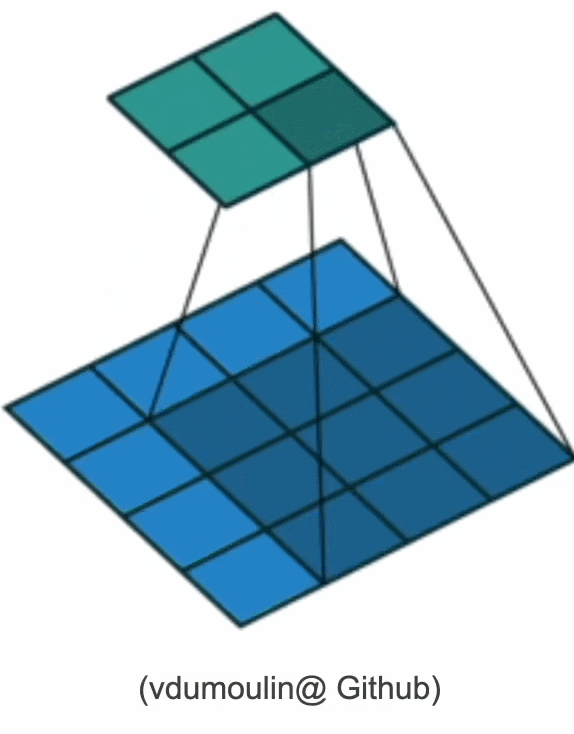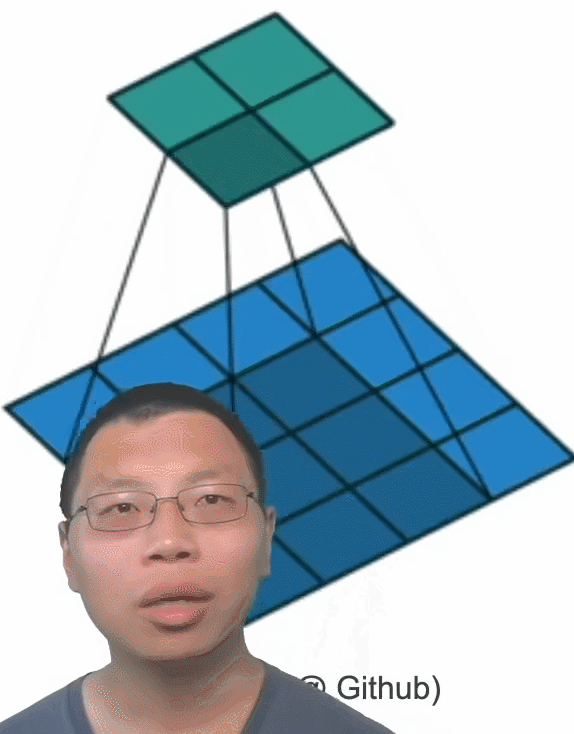
但参数大幅减少的代价是，我们的每一层只包含局部的信息，所有的权重学习都将依赖于归纳偏置。当这种偏置和现实不符时，如当图像不满足平移不变性时，我们的模型可能难以拟合我们的训练数据。

二、图像卷积

互相关运算

严格来说，卷积是一个错误的叫法，因为它所表达的运算其实是互相关运算(cross-correlation)，而不是卷积运算。

首先，我们暂时忽略通道（第三维）。在下图中，输入是高度为 3、宽度为 3 的二维张量。卷积核的高度和宽度都是 2，而卷积核窗口的形状由内核的高度和宽度决定。

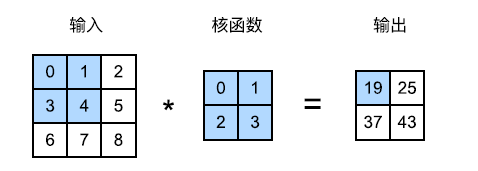
图6.2.1 二维互相关运算

以输出矩阵中左上角的 19 为例，其计算过程为相应部分输入矩阵与核函数的点积之和，即 $0\times0+1\times1+3\times2+4\times3=19$ 。

在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。

卷积层

卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。

就像我们之前随机初始化全连接层一样，在训练含有卷积层的模型时，我们也随机初始化卷积核权重。

为了应对较为复杂的卷积核，我们不可能手动设计滤波器，因此，我们也可以把卷积核当成学习的对象。

三、填充和步幅

在图6.2.1中，输入的高度和宽度都是 3，卷积核的高度和宽度都为 2，生成的输出表征的维数是 2$\times$2。

假设输入形状为 $n_h\times n_w$ ，卷积核形状为 $k_h\times k_w$ ，那么输出形状将是 $(n_h-k_h+1)\times(n_w-k_w+1)$ 。因此，卷积的输出形状取决于输入形状和卷积核的形状。

当我们应用了连续的卷积之后，最终得到的输出将原小于输入大小。比如，一个 240$\times $240 像素的图像，经过 10 层 5$ \times $5 的卷积后，将减少到 200$ \times$200像素。

如此一来，原始图像的边界丢失了很多有用的信息。而填充(padding)可以帮助我们解决这个问题。

此外，有时我们可能希望大幅降低图像的宽度和高度，而步幅(stride)可以在此提供帮助。

填充

为解决连续卷积层的丢失像素问题，我们引入填充：在输入图像的边界填充元素（通常填充 0）。

例如下图，将 3$\times $3 输入填充到 5$ \times $5 ，那么它的输出就增加为 4$ \times$4。

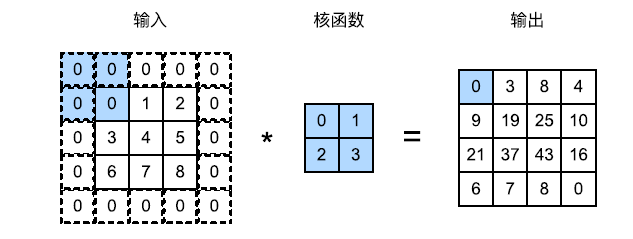
带填充的二维互相关

一般卷积核的高度和宽度为奇数，例如 1、3 或 5。这样可以在保持空间维度的同时，在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。

步幅

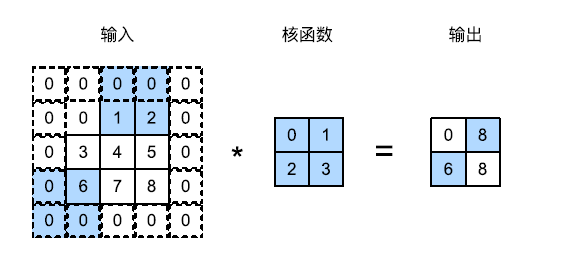
在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。前面的示例中，我们默认每次滑动一个元素。

但是，为了高效计算或者缩减采样次数，卷积窗口可以每次滑动多个元素。每次滑动元素的数量称为步幅。

垂直步幅为 3，水平步幅为 2 的二维互相关运算

四、多输入和多输出通道

之前我们使用过 Fashion-MNIST 数据集，其包含的图像是 28$\times $28 灰度图像。实际上，它并非是一个二维图像，在计算机中，其形状应为 28$ \times $28$ \times$1。

这个大小为 1 的轴称为通道(channel)维度，即灰度图像是单通道图片，每个像素仅由一个数值表示，用于表征黑的程度。

而彩色图片的通道数为 3，每个像素点由 RGB 三个数值表示颜色。

多输入通道

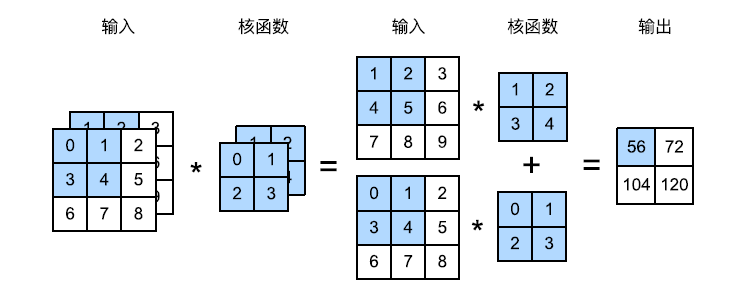
当输入包含多个通道时，需要构造一个与输入数据具有相同通道数的卷积核，以便与输入数据进行互相关运算。

各个通道执行互相关运算后，对应元素相加即可得到输出。

两个输入通道的互相关运算

多输出通道

对于多输出通道，我们可以直观理解为对输入图像的不同特征提取，例如一些通道专门识别边缘，另一些通道专门识别纹理等等。

在互相关运算中，每个输出通道先获取所有输入通道，再以对应该输出通道的卷积核计算出结果。

1$\times$1 卷积核

1$\times$1 的卷积没有起到卷积的作用：提取相邻像素间的相关特性。

但其却经常出现在复杂深层网络的设计中，主要在于其可以用于调整网络层的通道数量和控制模型复杂性，可视为一个全连接层，即每个输出都由所有输入得到。

五、池化（pooling）层

池化层也被称为汇聚层或采样层，其作用是基于局部性原理进行亚采样，从而在减少数据量的同时保留有用信息。

从直观上理解其作用为“汇聚”，反映到图片上，就是可以等比例缩小图片的尺寸。

与卷积层类似，汇聚层运算也是通过一个固定形状的窗口来进行，该窗口根据步幅大小在输入的所有区域内滑动，为固定窗口（汇聚窗口）计算一个输出。

我们通常计算汇聚窗口中所有相关元素的最大值或平均值，这些操作也分别称为最大汇聚层和平均汇聚层。

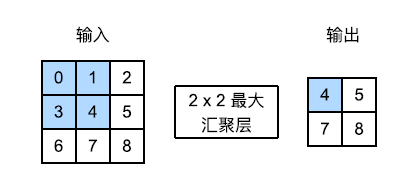
$2$\times$2 最大汇聚层$

汇聚层也可以设置填充和步幅来获得我们所需要的输出形状。

在处理多通道输入数据时，汇聚层在每个输入通道上单独运算，这意味着汇聚层的输出通道与输入通道数相同。

六、LeNet

LeNet 是最早发布的卷积神经网络之一，因其在计算机视觉任务中的高效性能而受到广泛关注。

时至今日，一些自动取款机仍然还在使用 LeNet 来帮助识别支票的数字。

从总体来看，LeNet（LeNet-5）由两个部分组成：

卷积编码器：由两个卷积层组成；
全连接层密集块：由三个全连接层组成。

其架构如下图所示。

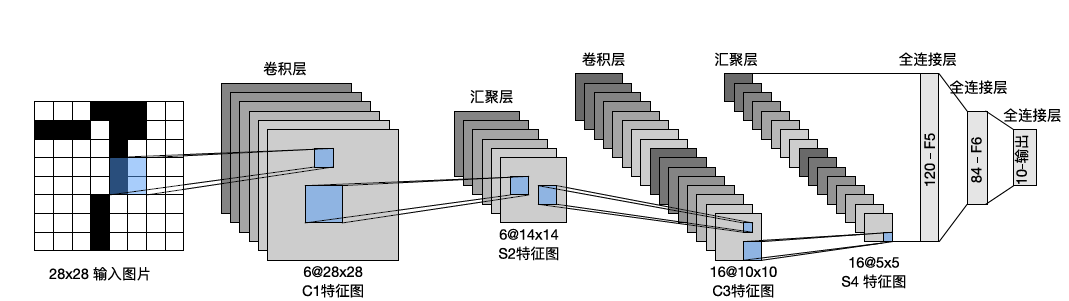
图6.6.1 LeNet 中的数据流

每个卷积块中的基本单元是一个卷积层、一个 sigmoid 激活函数和一个平均汇聚层。

每个卷积层使用 5$\times$5 大小的卷积核，故每经过一层卷积层，图片尺寸减少 4。

汇聚层窗口大小为 2$\times$2，采样后可将维数减少 4 倍。

第一卷积层有 6 个输出通道，第二卷积层有 16 个输出通道。

输出的通道数是可以自行设定的，没有太多道理。

为了将卷积块的输出传递给稠密块，我们必须进行展平操作。16 个通道，5$\times $5 的输入展平为 1$ \times$400，随后通过 3 层全连接层得到维度为 10 的输出，对应于分类结果的数量。

下面我们看看 LeNet 模型在 Fashion-MNIST 数据集上的效果如何。

定义模型

根据图6.6.1中的各层图示，可以很轻松地通过实例化Sequential得到。

    net = nn.Sequential(      # LeNet模型
        nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
        nn.AvgPool2d(kernel_size=2, stride=2),
        nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
        nn.AvgPool2d(kernel_size=2, stride=2),
        nn.Flatten(),
        nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
        nn.Linear(120, 84), nn.Sigmoid(),
        nn.Linear(84, 10))

训练模型

优化器与损失函数我们分别采用随机梯度下降和交叉熵，训练过程和前面类似，前馈、计算损失、反馈、更新，详细见附件代码。

训练了 10 轮后的训练损失、精度和测试精度为：

第10轮的训练损失为0.458
第10轮的训练精度为0.827
第10轮的测试集精度为0.823

关于卷积神经网络的内容总体上看是比较难啃的，有点抽象，不过多看看书和视频教程，还是可以理解到一些的。

最近发现李宏毅老师讲的很好，可以多看看。

LeNet模型训练代码见资源。