C语言-数据结构 无向图普里姆Prim算法（邻接矩阵存储）

news2024/9/20 12:16:00

        Prim算法使用了贪心的思想，在算法中使用了两个数组，这两个数组会非常巧妙的操作整个算法的灵魂过程

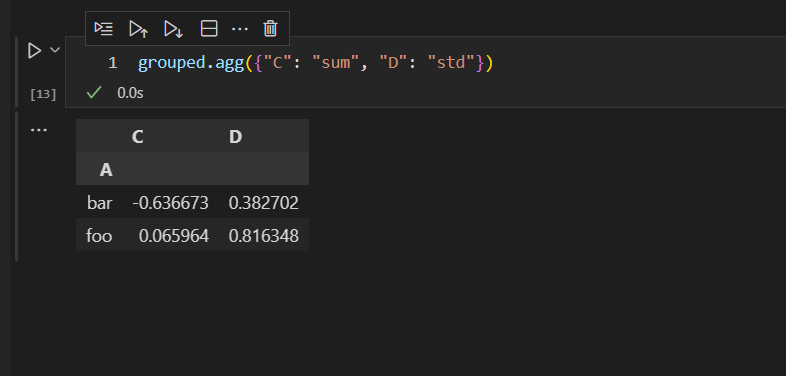
lowcost的功能：

1.帮助算法寻找到当前距离已完成的最小生成树集合的最小的边长（找到新边）

2.在整个过程中记录新结点加入的时候，更新整个已完成的生成树中所有结点集合到剩余各个结点的最小值（更新当前已加入最小生成树结点集合状态下距离其他结点最短边值）

adjvex的功能：

1.存储每个新节点加入已完成最小生成树结点时，通过它找到当前新加入生成树结点集合中的前驱结点是谁，从而输出对应的边

2.更新前驱结点，帮助在下一次寻找到新结点保存对应的前驱结点（例如A->B这条边中A结点叫前驱）

        整个算法的过程时非常巧妙的，lowcost数组类似于水母的触手一开始就只有一条触手，通过触手找到当前最短的边，并把它捕获到已经完成的生成树结点中，理解为生成新的一条触手，触手数量+1，整个代码中大for循环中包含两个小循环，大for循环进行节点数-1轮，每一次从图中找到一个新结点，也就是找到最小生成树的一条边，里面第一个while循环找到当前距离水面触手最短的结点，也就是即将加入的最小生成树的边，找到后并把边对应的结点设置为0标记已经找到的边，下面的小循环for是为了更新当新的触手（新的边）加入的时候，整个水母触手（已完成的最小生成树）距离剩下的各结点之间最短的边长进行更新。并存入下一个即将加入水母触手伙伴的前驱结点，以便绘制打印出对应的边。

我们将创建下面的无向权值图：

  最小生成树示意图：

        邻接矩阵的绘制还是手动赋值上三角，并通过矩阵对称性生成整个邻接矩阵，其中最小生成树中需要用到权值，对应原本有边的地方之前我是用1表示，现在改成边对应的权值，之前的0表示没有边，现在改成99表示为无穷，其实应该换成更大的值以确保树的边权值都小于这个最大值，但为了方便对齐显示看邻接矩阵，就使用了比本图中各边长较大的99来表示最大值。

        Prim算法代码：

/* Prim算法生成最小生成树  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */
	/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for (i = 1; i < G.numNodes; i++)	/* 循环除下标为0外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	printf("\n最小生成树的边按顺序生成：\n");
	for (i = 1; i < G.numNodes; i++)
	{
		min = GRAPH_INFINITY;	/* 初始化最小权值为∞， */
		/* 通常设置为不可能的大数字如32767、65535等 */
		j = 0; k = 0;
		while (j < G.numNodes)	/* 循环全部顶点 */
		{
			if (lowcost[j] != 0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for (j = 0; j < G.numNodes; j++)	/* 循环所有顶点 */
		{
			if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
			{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

完整代码（包含邻接矩阵的创建，Prim算法）

#include "stdio.h"    
#include "stdlib.h"   
#include "math.h"  
#include "time.h"

// 禁用特定的警告
#pragma warning(disable:4996)

// 定义一些常量和数据类型
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXVEX 8 /* 最大顶点数，用户定义 */
#define GRAPH_INFINITY 99 /* 用0表示∞，表示不存在边 */

/* 定义状态、顶点和边的类型 */
typedef int Status;  /* Status是函数的返回类型，如OK表示成功 */
typedef char VertexType; /* 顶点的类型，用字符表示 */
typedef int EdgeType; /* 边上的权值类型，用整数表示 */
typedef int Boolean; /* 布尔类型 */

/* 访问标记数组 */
Boolean visited[MAXVEX];

/* 图的邻接矩阵结构体 */
typedef struct
{
	VertexType vexs[MAXVEX]; /* 顶点表 */
	EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵，表示边的权值 */
	int numNodes, numEdges; /* 图中当前的顶点数和边数 */
} MGraph;

/* 创建一个无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph* G)
{
	int i, j, k, w;

	// 初始化图的顶点数和边数
	G->numNodes = 8;
	G->numEdges = 12;

	// 定义顶点标签
	char Array[] = "ABCDEFGHI";

	// 初始化邻接矩阵和顶点表
	for (i = 0; i < G->numNodes; i++) {
		for (j = 0; j < G->numNodes; j++) {
			G->arc[i][j] = GRAPH_INFINITY; /* 初始化邻接矩阵为∞ */
		}
		G->vexs[i] = Array[i]; /* 初始化顶点表 */
	}

	G->arc[0][0] = GRAPH_INFINITY;
	G->arc[0][1] = 10;
	G->arc[0][2] = GRAPH_INFINITY;
	G->arc[0][3] = GRAPH_INFINITY;
	G->arc[0][4] = GRAPH_INFINITY;
	G->arc[0][5] = 11;
	G->arc[0][6] = GRAPH_INFINITY;
	G->arc[0][7] = GRAPH_INFINITY;

	G->arc[1][0] = GRAPH_INFINITY;
	G->arc[1][1] = GRAPH_INFINITY;
	G->arc[1][2] = 23;
	G->arc[1][3] = GRAPH_INFINITY;
	G->arc[1][4] = GRAPH_INFINITY;
	G->arc[1][5] = GRAPH_INFINITY;
	G->arc[1][6] = 12;
	G->arc[1][7] = GRAPH_INFINITY;

	G->arc[2][0] = GRAPH_INFINITY;
	G->arc[2][1] = GRAPH_INFINITY;
	G->arc[2][2] = GRAPH_INFINITY;
	G->arc[2][3] = 21;
	G->arc[2][4] = GRAPH_INFINITY;
	G->arc[2][5] = GRAPH_INFINITY;
	G->arc[2][6] = GRAPH_INFINITY;
	G->arc[2][7] = GRAPH_INFINITY;

	G->arc[3][0] = GRAPH_INFINITY;
	G->arc[3][1] = GRAPH_INFINITY;
	G->arc[3][2] = GRAPH_INFINITY;
	G->arc[3][3] = GRAPH_INFINITY;
	G->arc[3][4] = GRAPH_INFINITY;
	G->arc[3][5] = GRAPH_INFINITY;
	G->arc[3][6] = GRAPH_INFINITY;
	G->arc[3][7] = 11;

	G->arc[4][0] = GRAPH_INFINITY;
	G->arc[4][1] = GRAPH_INFINITY;
	G->arc[4][2] = GRAPH_INFINITY;
	G->arc[4][3] = GRAPH_INFINITY;
	G->arc[4][4] = GRAPH_INFINITY;
	G->arc[4][5] = 47;
	G->arc[4][6] = GRAPH_INFINITY;
	G->arc[4][7] = 80;

	G->arc[5][0] = GRAPH_INFINITY;
	G->arc[5][1] = GRAPH_INFINITY;
	G->arc[5][2] = GRAPH_INFINITY;
	G->arc[5][3] = GRAPH_INFINITY;
	G->arc[5][4] = GRAPH_INFINITY;
	G->arc[5][5] = GRAPH_INFINITY;
	G->arc[5][6] = 6;
	G->arc[5][7] = GRAPH_INFINITY;

	G->arc[6][0] = GRAPH_INFINITY;
	G->arc[6][1] = GRAPH_INFINITY;
	G->arc[6][2] = GRAPH_INFINITY;
	G->arc[6][3] = GRAPH_INFINITY;
	G->arc[6][4] = GRAPH_INFINITY;
	G->arc[6][5] = GRAPH_INFINITY;
	G->arc[6][6] = GRAPH_INFINITY;
	G->arc[6][7] = 8;

	G->arc[7][0] = GRAPH_INFINITY;
	G->arc[7][1] = GRAPH_INFINITY;
	G->arc[7][2] = GRAPH_INFINITY;
	G->arc[7][3] = GRAPH_INFINITY;
	G->arc[7][4] = GRAPH_INFINITY;
	G->arc[7][5] = GRAPH_INFINITY;
	G->arc[7][6] = GRAPH_INFINITY;
	G->arc[7][7] = GRAPH_INFINITY;

	// 由于是无向图，邻接矩阵是对称的，需要将其对称
	for (int i = 0; i < G->numNodes; i++) {
		for (int j = 0; j < G->numNodes; j++) {
			G->arc[j][i] = G->arc[i][j];
		}
	}

	// 打印邻接矩阵
	printf("邻接矩阵为：\n");
	printf("     ");
	for (int i = 0; i < G->numNodes; i++) {
		printf("%2d ", i); /* 打印列索引 */
	}
	printf("\n     ");
	for (int i = 0; i < G->numNodes; i++) {
		printf("%2c ", G->vexs[i]); /* 打印顶点标签 */
	}
	printf("\n");
	for (int i = 0; i < G->numNodes; i++) {
		printf("%2d", i); /* 打印行索引 */
		printf("%2c ", G->vexs[i]); /* 打印顶点标签 */
		for (int j = 0; j < G->numNodes; j++) {
			if (G->arc[i][j] != 99) {
				printf("\033[31m%02d \033[0m", G->arc[i][j]); /* 打印邻接矩阵中的权值 */
			}
			else {
				printf("%02d ", G->arc[i][j]); /* 打印邻接矩阵中的权值 */
			}
		}
		printf("\n");
	}
}

/* Prim算法生成最小生成树  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */
	/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for (i = 1; i < G.numNodes; i++)	/* 循环除下标为0外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	printf("\n最小生成树的边按顺序生成：\n");
	for (i = 1; i < G.numNodes; i++)
	{
		min = GRAPH_INFINITY;	/* 初始化最小权值为∞， */
		/* 通常设置为不可能的大数字如32767、65535等 */
		j = 0; k = 0;
		while (j < G.numNodes)	/* 循环全部顶点 */
		{
			if (lowcost[j] != 0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for (j = 0; j < G.numNodes; j++)	/* 循环所有顶点 */
		{
			if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
			{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

int main(void)
{
	MGraph G;
	/* 创建图 */
	CreateMGraph(&G);
	//Prim算法
	MiniSpanTree_Prim(G);
	return 0;
}

最小生成树示意图：

运行结果，边是按下标输出的，下标所对应的字母按ABCDEFGH顺序来表示：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2108706.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

分拣机介绍及解决方案细节

分拣机介绍及解决方案细节

导语 大家好&#xff0c;我是社长&#xff0c;老K。专注分享智能制造和智能仓储物流等内容。 新书《智能物流系统构成与技术实践》人俱乐部 完整版文件和更多学习资料&#xff0c;请球友到知识星球【智能仓储物流技术研习社】自行下载。 这份文件是关于交叉带式分拣机的介绍及解…
阅读更多...
openSSL 如何降版本

openSSL 如何降版本

文章目录 前言openSSL 如何降版本1. 卸载2. 安装新的openssl版本3. 验证 前言 如果您觉得有用的话&#xff0c;记得给博主点个赞&#xff0c;评论&#xff0c;收藏一键三连啊&#xff0c;写作不易啊^ _ ^。   而且听说点赞的人每天的运气都不会太差&#xff0c;实在白嫖的话&…
阅读更多...
RT-Thread 使用HTTP固件下载方式进行OTA远程升级

RT-Thread 使用HTTP固件下载方式进行OTA远程升级

参考资料:RT-T官网资料如下链接所示 STM32通用Bootloader (rt-thread.org) 1.app程序env配置过程 参考上述资料中"制作 app 固件"章节&#xff0c;分区大小根据自己设备而定&#xff0c;以下是我以407VET6为例设置的fal分区 notes:上述分区是由片内flash(on-chip)…
阅读更多...
机械革命imini Pro820迷你主机评测和拆解，8845H小主机使用政府补贴仅需两千三

机械革命imini Pro820迷你主机评测和拆解，8845H小主机使用政府补贴仅需两千三

机械革命imini Pro820迷你主机评测和拆解&#xff0c;8845H小主机使用政府补贴仅需两千三。 最近上线了家电补贴相关的活动&#xff0c;最高可以补贴20%&#xff0c;然后就看到了这款mini主机感觉很划算就下单了&#xff0c;用来替换我旧的N5095小主机&#xff0c;当服务器用。…
阅读更多...
电子技术基础

电子技术基础

目录 二极管 二极管的概念二极管的整流 二极管的防反接 二极管的钳位稳压二极管 三极管 NPN型三极管PNP型三极管三极管的三种状态三极管三个极之间电流的关系 放大电路 三极管共射极放大电路分压式偏置电路静态工作点多级放大功率放大电路 运算放大器 同相比例放大器反相…
阅读更多...
旅行商问题 | Matlab基于混合粒子群算法GA-PSO的旅行商问题TSP

旅行商问题 | Matlab基于混合粒子群算法GA-PSO的旅行商问题TSP

目录 效果一览基本介绍建模步骤程序设计参考资料 效果一览 基本介绍 混合粒子群算法GA-PSO是一种结合了遗传算法&#xff08;Genetic Algorithm, GA&#xff09;和粒子群优化算法&#xff08;Particle Swarm Optimization, PSO&#xff09;的优化算法。在解决旅行商问题&#…
阅读更多...
「Python数据分析」Pandas进阶，使用groupby分组聚合数据（三）

「Python数据分析」Pandas进阶，使用groupby分组聚合数据（三）

​在实际数据分析和处理过程中&#xff0c;我们可能需要灵活对分组数据进行聚合操作。这个时候&#xff0c;我们就需要用到用户自定义函数&#xff08;User-Defined Functions&#xff0c;UDFs&#xff09;。 使用用户自定义函数进行聚合 使用用户自定义函数聚合时的性能&…
阅读更多...
联想泄露显示本月推出更便宜的Copilot Plus电脑

联想泄露显示本月推出更便宜的Copilot Plus电脑

联想似乎准备推出新的更实惠的 Copilot Plus 电脑。可靠的爆料者Evan Blass发布了一份来自联想的新闻稿&#xff0c;详细介绍了将在本周晚些时候的IFA展会上宣布的各种Copilot Plus电脑&#xff0c;其中包括两款采用尚未公布的8核高通骁龙X Plus芯片的电脑。 这些新的高通芯片…
阅读更多...
Qt 创建一个json数组对象写入文档并从文档读出q

Qt 创建一个json数组对象写入文档并从文档读出q

void createJsonArray() { // 创建一个JSON数组 QJsonArray jsonArray; // 创建一些JSON对象并添加到数组中 for (int i 0; i < 3; i) { QJsonObject jsonObject; jsonObject["key" QString::number(i)] "value" QStri…
阅读更多...
原点安全荣获“AutoSec Awards 安全之星”优秀汽车数据安全合规方案奖

原点安全荣获“AutoSec Awards 安全之星”优秀汽车数据安全合规方案奖

9月3日&#xff0c;「AutoSec 2024第八届中国汽车网络安全周暨第五届智能汽车数据安全展」在上海盛大开幕。本届大会由谈思实验室和谈思汽车主办、上海市车联网协会联合主办&#xff0c;以汽车“网络数据安全、软件安全、功能安全”为主题&#xff0c;汇聚了国内外的技术专家、…
阅读更多...
Meta关闭Spark AR平台：未来规划与影响分析

Meta关闭Spark AR平台：未来规划与影响分析

Meta宣布将关闭其移动AR创作平台Spark AR&#xff0c;这一消息在业界引起了广泛关注。尽管Snap和TikTok在AR滤镜领域取得了巨大成功&#xff0c;但Meta却选择了另一条发展道路。本文将探讨这一决策背后的可能原因及其对未来的影响。 关闭Spark AR平台的背后 硬件为主&#xff…
阅读更多...
PyTorch 创建数据集

PyTorch 创建数据集

图片数据和标签数据准备 1.本文所用图片数据在同级文件夹中 ,文件路径为train/’ 2.标签数据在同级文件&#xff0c;文件路径为train.csv 3。将标签数据提取 train_csvpd.read_csv(train.csv)创建继承类 第一步&#xff0c;首先创建数据类对象 此时可以想象为单个数据单元的…
阅读更多...
【PyTorch】基础环境如何打开

【PyTorch】基础环境如何打开

前期安装可以基于这个视频&#xff0c;本文是为了给自己存档如何打开pycharm和jupyter notebookPyTorch深度学习快速入门教程&#xff08;绝对通俗易懂&#xff01;&#xff09;【小土堆】_哔哩哔哩_bilibili Pycharm 配置 新建项目的时候选择解释器pytorch-gpu即可。 Jupyte…
阅读更多...
【C++ 第二十二章】C++的类型转换

【C++ 第二十二章】C++的类型转换

1.C语言中的类型转换 在C语言中&#xff0c;如果赋值运算符左右两侧类型不同&#xff0c;或者形参与实参类型不匹配&#xff0c;或者返回值类型与接收返回值类型不一致时&#xff0c;就需要发生类型转化&#xff0c;C语言中总共有两种形式的类型转换&#xff1a;隐式类型转换和…
阅读更多...
CDA数据分析一级考试备考攻略

CDA数据分析一级考试备考攻略

一、了解考试内容和结构 CDA一级考试主要涉及的内容包括&#xff1a;数据分析概述与职业操守、数据结构、数据库基础与数据模型、数据可视化分析与报表制作、Power BI应用、业务数据分析与报告编写等。 CDA Level Ⅰ 认证考试大纲:https://www.cdaglobal.com/certification.h…
阅读更多...
一文还原时序数据库 IoTDB 在 TPCx-IoT 的测试全流程！

一文还原时序数据库 IoTDB 在 TPCx-IoT 的测试全流程！

在云服务硬件环境下&#xff0c;IoTDB 写入、查询、利用资源能力均表现出色&#xff01; 之前&#xff0c;我们为大家介绍了基于 IoTDB 的企业级产品 TimechoDB&#xff0c;在 TPCx-IoT 基准测试中打破世界纪录&#xff0c;取得的双指标第一成绩&#xff0c;和选择 TPCx-IoT 的…
阅读更多...
【Python机器学习】核心数、进程、线程、超线程、L1、L2、L3级缓存

【Python机器学习】核心数、进程、线程、超线程、L1、L2、L3级缓存

如何知道自己电脑的CPU是几核的，打开任务管理器（同时按下：Esc键、SHIFT键、CTRL键） 然后，点击任务管理器左上角的性能选项，观察右下角中的内核：后面的数字，就是你CPU的核心数，下图中我的是16个核心的。 需要注意的是，下面的逻辑处理器：32 表示支持 32 线程（即超线…
阅读更多...
【爬虫软件】批量采集短视频博主的主页作品

【爬虫软件】批量采集短视频博主的主页作品

用python开发的DY爬虫采集软件&#xff0c;可自动按博主抓取其已发布视频数据。 软件界面&#xff1a; 采集结果: 日志记录&#xff1a; 软件说明&#xff1a; 演示视频&#xff1a; https://www.bilibili.com/video/BV1Kb42187qf 讲解文章&#xff1a; https://www.bi…
阅读更多...
2024数学建模国赛选题建议+团队助攻资料

2024数学建模国赛选题建议+团队助攻资料

目录 一、题目特点和选题建议 二、模型选择 1、评价模型 2、预测模型 3、分类模型 4、优化模型 5、统计分析模型 三、white学长团队助攻资料 1、助攻代码 2、成品论文PDF版 3、成品论文word版 9月5日晚18&#xff1a;00就要公布题目了&#xff0c;根据历年竞赛题目…
阅读更多...
QT: Unable to create a debugging engine.

QT: Unable to create a debugging engine.

1.问题场景&#xff1a; 第一次安装QT&#xff0c;没有配置debug功能 打开控制面板》程序》找到Kit 重启电脑即可 2.问题场景&#xff1a; qt原本一直好好的&#xff0c;突然有天打开运行调试版本&#xff0c;提示Unable to create a debugging engine.错误。这个是指无法创…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023