全网最适合入门的面向对象编程教程：45 Python实现常见数据结构-链表、树、哈希表、图和堆

全网最适合入门的面向对象编程教程：45 Python 实现常见数据结构-链表、树、哈希表、图和堆

摘要：

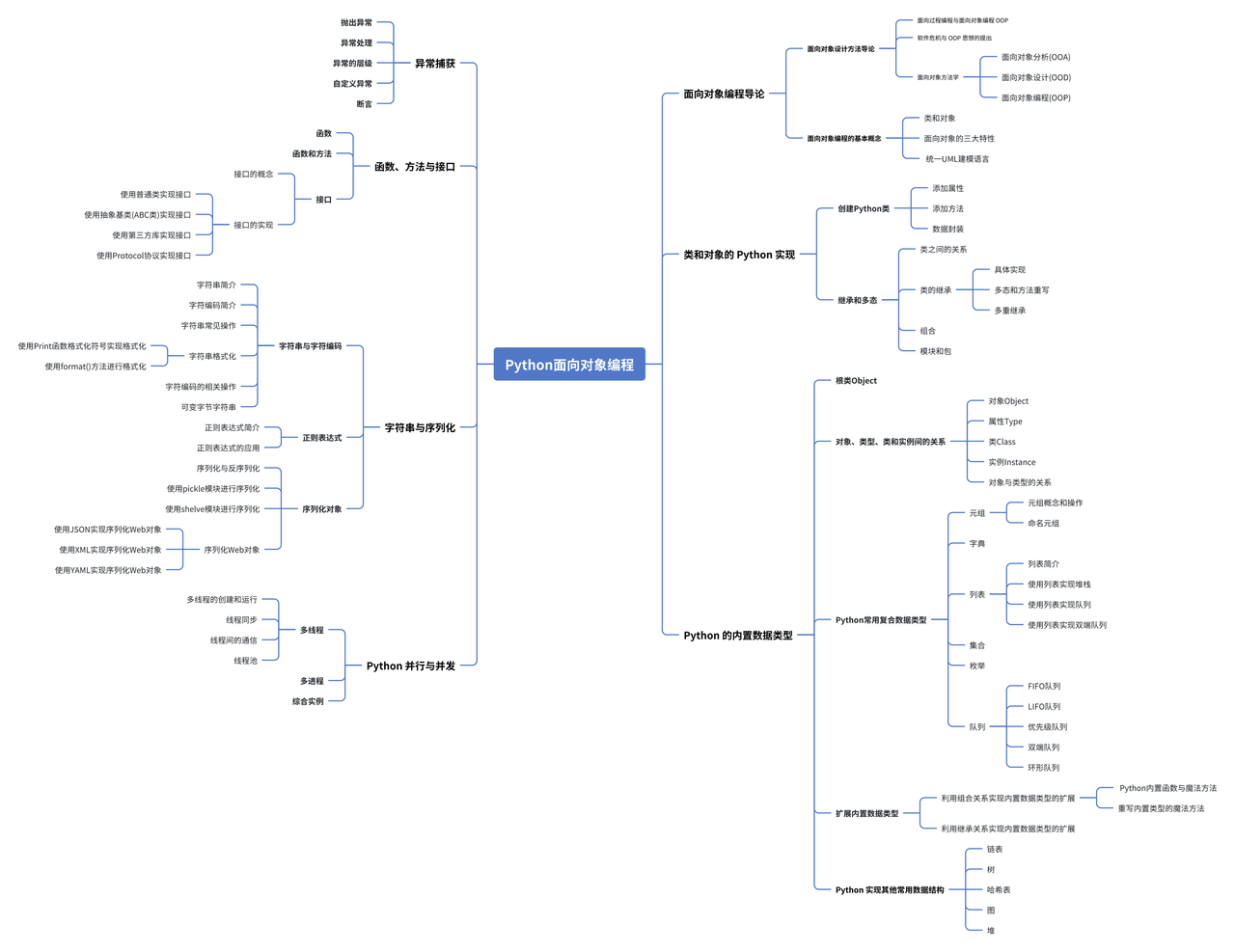
数据结构是计算机科学中的一种组织和存储数据的方式，它决定了数据的访问方式和操作效率，数据结构的选择和实现对程序的性能和设计至关重要。本文主要讲述了如何使用 Python 语言和内置库实现常见数据结构。

原文链接：

FreakStudio的博客

往期推荐：

可能是全网最适合入门的面向对象编程教程：Python实现-嵌入式爱好者必看！

全网最适合入门的面向对象编程教程：00 面向对象设计方法导论

全网最适合入门的面向对象编程教程：01 面向对象编程的基本概念

全网最适合入门的面向对象编程教程：02 类和对象的Python实现-使用Python创建类

全网最适合入门的面向对象编程教程：03 类和对象的Python实现-为自定义类添加属性

全网最适合入门的面向对象编程教程：04 类和对象的 Python 实现-为自定义类添加方法

全网最适合入门的面向对象编程教程：05 类和对象的Python实现-PyCharm代码标签

全网最适合入门的面向对象编程教程：06 类和对象的 Python 实现-自定义类的数据封装

全网最适合入门的面向对象编程教程：07 类和对象的Python实现-类型注解

全网最适合入门的面向对象编程教程：08 类和对象的 Python 实现-@property 装饰器

全网最适合入门的面向对象编程教程：09 类和对象的Python实现-类之间的关系

全网最适合入门的面向对象编程教程：10 类和对象的Python实现-类的继承和里氏替换原则

全网最适合入门的面向对象编程教程：11 类和对象的Python实现-子类调用父类方法

全网最适合入门的面向对象编程教程：12 类和对象的 Python 实现-Python 使用 logging 模块输出程序运行日志

全网最适合入门的面向对象编程教程：13 类和对象的 Python 实现-可视化阅读代码神器 Sourcetrail 的安装使用

全网最适合入门的面向对象编程教程：14 类和对象的Python实现-类的静态方法和类方法

全网最适合入门的面向对象编程教程：15 类和对象的Python实现-__slots__魔法方法

全网最适合入门的面向对象编程教程：16 类和对象的Python实现-多态、方法重写与开闭原则

全网最适合入门的面向对象编程教程：17 类和对象的Python实现-鸭子类型与“file-like object“

全网最适合入门的面向对象编程教程：18 类和对象的Python实现-多重继承与PyQtGraph串口数据绘制曲线图

全网最适合入门的面向对象编程教程：19 类和对象的 Python 实现-使用 PyCharm 自动生成文件注释和函数注释

全网最适合入门的面向对象编程教程：20 类和对象的 Python 实现-组合关系的实现与 CSV 文件保存

全网最适合入门的面向对象编程教程：21 类和对象的 Python 实现-多文件的组织：模块 module 和包 package

全网最适合入门的面向对象编程教程：22 异常捕获-异常和语法错误

全网最适合入门的面向对象编程教程：23 异常捕获-抛出异常

全网最适合入门的面向对象编程教程：24 异常捕获现-异常的捕获与处理：try/except语句、文件读写示例、Exception引用

全网最适合入门的面向对象编程教程：25 异常捕获-Python 判断输入数据类型

全网最适合入门的面向对象编程教程：26 异常捕获-上下文管理器和with语句

全网最适合入门的面向对象编程教程：27 异常捕获-Python 中异常层级与自定义异常类的实现

全网最适合入门的面向对象编程教程：28 异常捕获-Python编程原则、哲学和规范大汇总

全网最适合入门的面向对象编程教程：29 异常捕获-断言与防御性编程和help函数的使用

全网最适合入门的面向对象编程教程：30 Python的内置数据类型-object根类

全网最适合入门的面向对象编程教程：31 Python的内置数据类型-对象Object和类型Type

全网最适合入门的面向对象编程教程：32 Python的内置数据类型-类Class和实例Instance

全网最适合入门的面向对象编程教程：33 Python 的内置数据类型-对象 Object 和类型 Type 的关系

全网最适合入门的面向对象编程教程：34 Python的内置数据类型-Python常用复合数据类型：元组和命名元组

全网最适合入门的面向对象编程教程：35 Python的内置数据类型-文档字符串和__doc__属性

全网最适合入门的面向对象编程教程：36 Python的内置数据类型-字典

全网最适合入门的面向对象编程教程：37 Python常用复合数据类型-列表和列表推导式

全网最适合入门的面向对象编程教程：38 Python常用复合数据类型-使用列表实现堆栈、队列和双端队列

全网最适合入门的面向对象编程教程：39 Python 常用复合数据类型-集合

全网最适合入门的面向对象编程教程：40 Python 常用复合数据类型-枚举和 enum 模块的使用

全网最适合入门的面向对象编程教程：41 Python常用复合数据类型-队列（FIFO、LIFO、优先级队列、双端队列和环形队列）

全网最适合入门的面向对象编程教程：42 Python常用复合数据类型-collections容器数据类型

全网最适合入门的面向对象编程教程：43 Python常用复合数据类型-扩展内置数据类型

全网最适合入门的面向对象编程教程：44 Python内置函数与魔法方法-重写内置类型的魔法方法

文档和代码获取：

可访问如下链接进行对文档下载：

https://github.com/leezisheng/Doc

本文档主要介绍如何使用 Python 进行面向对象编程，需要读者对 Python 语法和单片机开发具有基本了解。相比其他讲解 Python 面向对象编程的博客或书籍而言，本文档更加详细、侧重于嵌入式上位机应用，以上位机和下位机的常见串口数据收发、数据处理、动态图绘制等为应用实例，同时使用 Sourcetrail 代码软件对代码进行可视化阅读便于读者理解。

相关示例代码获取链接如下：https://github.com/leezisheng/Python-OOP-Demo

正文

数据结构基本知识

实际上，前文讲到的队列、列表、集合、字典等均属于数据结构的一部分。数据结构，作为一种代码结构，其核心目的在于有序地存储与组织数据，进而简化信息的修改、导航与访问过程。它不仅决定了数据的收集方式、实现的功能以及数据间的相互关系，更在计算机科学和编程的各个领域，如操作系统、前端开发以及机器学习等，发挥着不可或缺的作用。数据结构是解决问题的高效且真实的关键构件。每一种数据结构都有其独特的适用场景和任务。

数据结构可划分为逻辑结构与物理结构两大类：

逻辑结构：是指数据元素间逻辑关系的数据组织方式，这种关系侧重于元素间的相对位置，而与数据在计算机中的实际存储位置无关。

在逻辑结构的分类中，可以分为线性结构和非线性结构：

物理结构：又称存储结构，描述的是数据逻辑结构在计算机存储空间中的具体实现形式。数据的逻辑结构通常可以映射为多种物理结构。物理结构是实现数据元素间逻辑关系的具体手段。一种逻辑结构可以根据实际需求转化为多种物理结构。常见的物理结构有：
- ① 顺序存储，其特点是元素在内存中的存储顺序是连续的，线性表的元素通过一组连续的存储单元来存储。
- ② 链式存储，在这种方式中，内存中的存储元素不必连续，每个元素节点包含数据元素和指向相邻元素的指针信息。
- ③ 索引存储，除了存储节点信息，还通过附加的索引表来标识节点的内存地址，索引表由多个索引项构成。
- ④ 散列存储，又称 Hash 存储，其中节点的存储地址由节点的关键码值直接决定。

接下来，我们将简要介绍如何利用面向对象编程的思维和 Python 内置数据类型去实现其他的数据结构，注意该部分并非本书重点内容，所以这里只是浅显的讲一下数据结构，其中实现代码主要是帮助读者理解而非实际应用。

Python 实现链表

链表是一种物理存储单元上非连续、非顺序的存储结构，是由许多相同数据类型的数据项按照特定顺序排列而成的线性表。链表有一系列节点组成，所谓节点就是指链表中的每一个元素，每个节点包含两个数据，一个是存储元素的数据域（值），另一个是存储下一个节点地址的指针域。

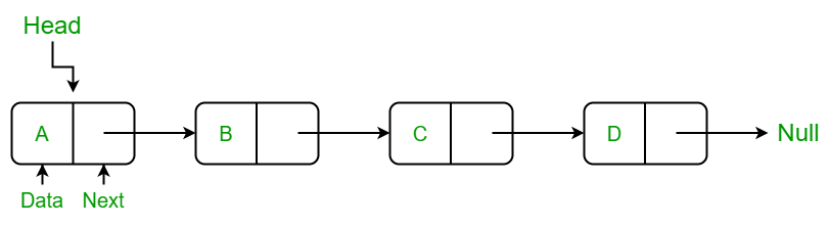
链表中的第一个节点称为头节点，最后一个节点称为尾节点，其中尾节点的 next 指向为 null。链表可以是单链，也可以是双链，这取决于每个节点是只有一个指向下一个节点的指针，还是还有一个指向前一个节点的指针。你可以把链表想象成一条链;单个链接只与相邻的链接有一个连接，但所有链接一起形成一个更大的结构。

class Node:
    def __init__(self, dataval=None):
        self.dataval = dataval
        self.nextval = None
class SLinkedList:
    def __init__(self):
        self.headval = None
list1 = SLinkedList()
list1.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
_# Link first Node to second node_
list1.headval.nextval = e2
_# Link second Node to third node_
e2.nextval = e3

链表具有以下优势：新元素插入和删除更高效、比数组更易于重组、高级数据结构 (如图形或树)都是基于链表的，缺点是：每个数据点的指针存储增加了内存使用量同时必须始终从头节点遍历链表以查找特定元素。

Python 实现树

树是另一种基于关系的数据结构，专门用于表示层次结构。与链表一样，它们也被 Node 对象填充，Node 对象包含一个数据值和一个或多个指针，用于定义其与直接节点的关系。每棵树都有一个根节点，所有其他节点都从根节点分支出来。根节点包含指向它正下方所有元素的指针，这些元素被称为它的子节点。这些子节点可以有它们自己的子节点。在同一层上的任何节点都称为同级节点。没有连接子节点的节点称为叶节点。

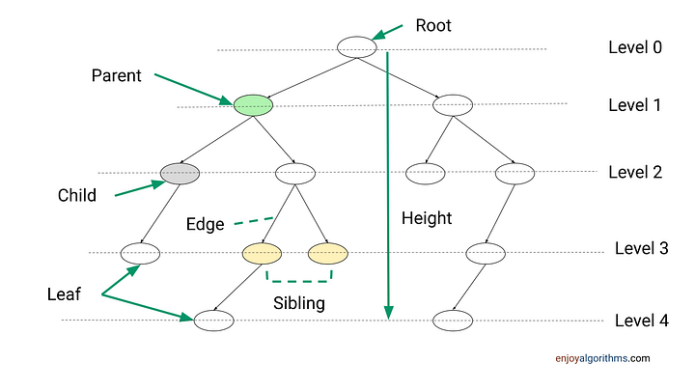
我们平时用到最多的就是二叉树，二叉树最常见的应用是二叉搜索树。二叉搜索树擅长于搜索大量的数据集合，因为时间复杂度取决于树的深度而不是节点的数量。二叉树具有以下特点：

左子树只包含元素小于根的节点。
右子树只包含元素大于根的节点。
左右子树也必须是二叉搜索树。他们必须以树的“根”来遵循上述规则。
不能有重复的节点，即不能有两个节点具有相同的值。

lass Node:
    def __init__(self, data):
        self.left = None
        self.right = None
        self.data = data
    def insert(self, data):
_# Compare the new value with the parent node_
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data
_# Print the tree_
    def PrintTree(self):
        if self.left:
            self.left.PrintTree()
        print( self.data),
        if self.right:
            self.right.PrintTree()
_# Use the insert method to add nodes_
root = Node(12)
root.insert(6)
root.insert(14)
root.insert(3)
root.PrintTree()

树形结构的搜索效率高非常适合存储分层数据（如文件位置等），但仅仅适用于排序的列表，未排序的数据退化为线性搜索。

Python 实现哈希表

哈希表又叫散列表，哈希表是一种复杂的数据结构，能够存储大量信息并有效检索特定元素。此结构存储的是由键(key)和值(value)组成的数据，根据键直接访问存储在内存存储位置的数据结构。

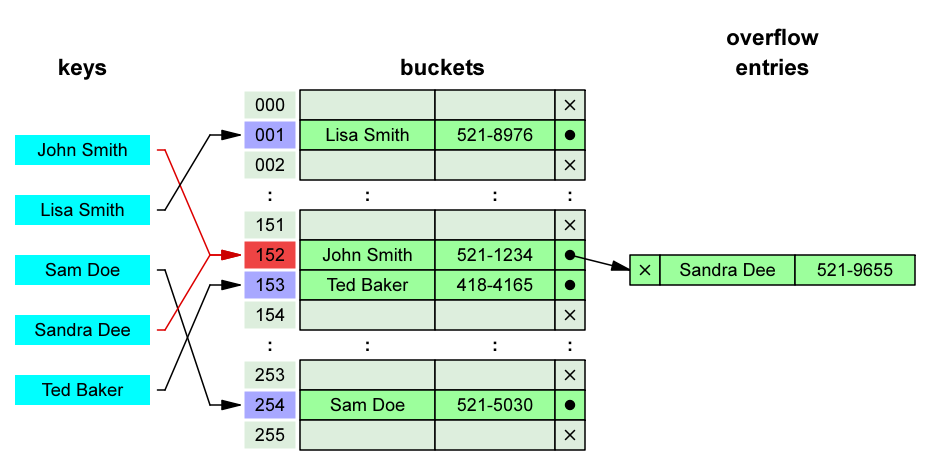
每个输入键都要经过一个哈希函数，该函数将其从初始形式转换为一个整数值，称为哈希。哈希函数必须始终从相同的输入产生相同的哈希，必须快速计算，并产生固定长度的值。Python 包含一个内置的 hash()函数，可以加速实现。然后，该表使用散列来查找所需值(称为存储桶)的一般位置。然后，程序只需要在这个子组中搜索所需的值，而不必搜索整个数据池。除了这个通用框架之外，根据应用程序的不同，哈希表也可能非常不同。有些可能允许来自不同数据类型的键，而有些可能有不同的设置桶或不同的散列函数。

下面是一个 Python 代码中的哈希表示例:

import pprint
class Hashtable:
    def __init__(self, elements):
        self.bucket_size = len(elements)
        self.buckets = [[] for i in range(self.bucket_size)]
        self._assign_buckets(elements)
    def _assign_buckets(self, elements):
        for key, value in elements: _#calculates the hash of each key_
            hashed_value = hash(key)
            index = hashed_value % self.bucket_size _# positions the element in the bucket using hash_
            self.buckets[index].append((key, value)) _#adds a tuple in the bucket_
    def get_value(self, input_key):
        hashed_value = hash(input_key)
        index = hashed_value % self.bucket_size
        bucket = self.buckets[index]
        for key, value in bucket:
            if key == input_key:
                return(value)
        return None
    def __str__(self):
        return pprint.pformat(self.buckets) _# pformat returns a printable representation of the object_
if __name__ == "__main__":
     capitals = [
        ('France', 'Paris'),
        ('United States', 'Washington D.C.'),
        ('Italy', 'Rome'),
        ('Canada', 'Ottawa')
    ]
hashtable = Hashtable(capitals)
print(hashtable)
print(f"The capital of Italy is {hashtable.get_value('Italy')}"

哈希表可以将任何形式的键隐藏为整数索引，对于大型数据集搜索非常有效，常常应用于用于频繁查询的大型数据库或根据关键字检索的系统。

Python 实现图

图是一种数据结构，用于表示数据顶点(图的节点)之间关系的可视化。将顶点连接在一起的链接称为边。边定义了哪些顶点被连接，但没有指明它们之间的流向。每个顶点与其他顶点都有连接，这些连接以逗号分隔的列表形式保存在顶点上。还有一种特殊的图叫做有向图，它定义了关系的方向，类似于链表。在建模单向关系或类似流程图的结构时，有向图很有帮助。

在 Python 中，图的最佳实现方式是使用字典，每个顶点的名称作为键，边列表作为值。

_# Create the dictionary with graph elements_
graph = { "a" : ["b","c"],
                 "b" : ["a", "d"],
                 "c" : ["a", "d"],
                  "d" : ["e"],
                  "e" : ["d"]
         }
_# Print the graph          _
print(graph)

图在存储数据上有着比较复杂和高效的算法，分别有邻接矩阵、邻接表、十字链表、邻接多重表、边集数组等存储结构。常见的图遍历算法就是广度优先算法和深度优先算法。它适用于网络或类似网络的结构建模，可以通过代码快速传达视觉信息，但是在大型图中很难理解顶点链接同时从图表中解析数据的时间昂贵。

Python 实现堆

堆比较特殊，是一种图的树形结构。被用于实现“优先队列”(priority queues)，优先队列是一种数据结构，可以自由添加数据，但取出数据时要从最小值开始按顺序取出。在堆的树形结构中，各个顶点被称为“结点”(node)，数据就存储在这些结点中。只要满足下面两个特点的树形结构就是堆：

堆是一个完全二叉树（所谓完全二叉树就是除了最后一层其他层的节点个数都是满的）。
堆中每一个节点的值都必须大于等于或者小于其子树中每一个节点的值。

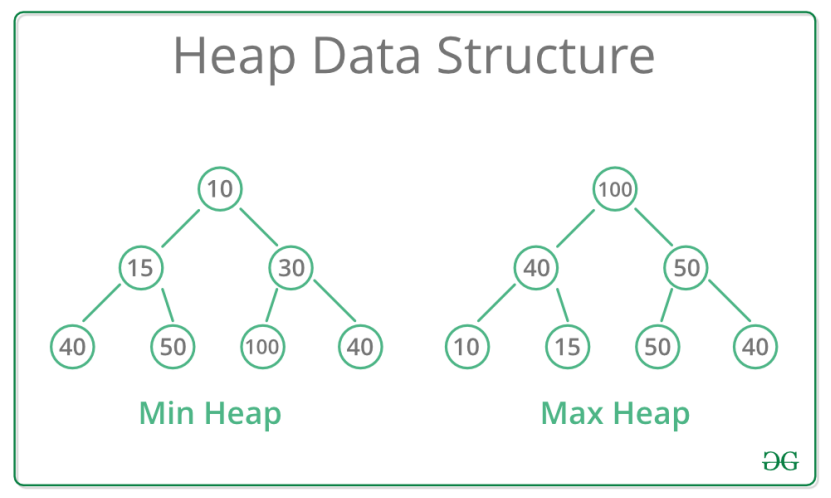
我们可以使用 heapq 模块实现一个适合与 Python 的列表一起使用的最小堆：

import heapq
from heapq_showtree import show_tree
from heapq_heapdata import data

heap = []
print('random :', data)
print()

for n in data:
    print('add {:>3}:'.format(n))
    heapq.heappush(heap, n)
    show_tree(heap)