摘要

本文介绍了快速探索随机树（Rapidly-exploring Random Tree, RRT）算法在二维环境中的路径规划应用。RRT是一种随机采样算法，能够快速构建从起点到目标点的路径，特别适用于复杂环境中的机器人路径规划。通过在随机方向上扩展树结构，RRT算法能够高效避开障碍物并找到一条可行路径。

理论

RRT算法通过不断随机采样空间中的节点，并尝试将当前树扩展到这些节点，逐步构建一条从起点到目标点的路径。其关键步骤包括：

1. 随机采样：在环境中随机采样一个点，作为树扩展的方向。

2. 树扩展：尝试从当前树的一个节点向采样点扩展，生成一个新节点。

3. 避障检测：检查新节点是否与障碍物发生碰撞，如果发生则放弃该节点。

4. 路径生成：不断重复上述步骤，直到树包含了目标点，从而生成一条可行路径。

实验结果

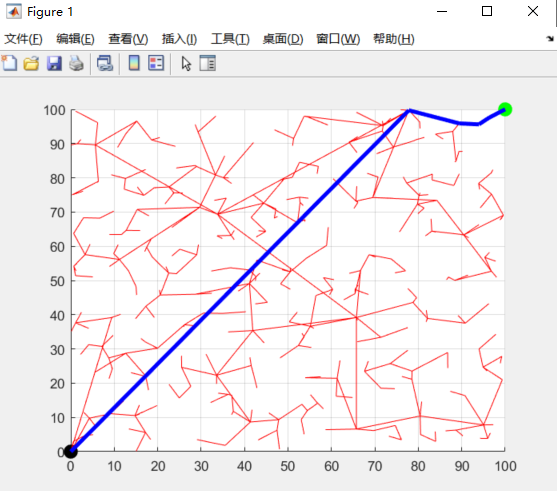
实验使用RRT算法在二维环境中进行路径规划测试，结果显示算法能够快速生成路径并有效避开环境中的障碍物。以下是实验的主要发现：

• 路径生成速度：RRT能够在较短时间内生成路径，适合实时应用。

• 避障性能：算法能够在复杂障碍环境中找到可行路径，但生成的路径可能不够平滑。

• 优化潜力：通过对路径进行后续优化处理（如RRT*），可以进一步改善路径的平滑性和总长度。

  

部分代码

% Define map and parameters
mapSize = [0, 50, 0, 50]; % Map size [xmin, xmax, ymin, ymax]
startPos = [5, 5]; % Start position
goalPos = [45, 45]; % Goal position
maxStep = 2; % Maximum step size

% Initialize RRT
nodes = startPos; % Start node
edges = []; % Edge list

% Main RRT loop
while norm(nodes(end,:) - goalPos) > 1
    % Random sampling
    randPoint = [rand * (mapSize(2) - mapSize(1)), rand * (mapSize(4) - mapSize(3))];
    
    % Find nearest node
    [~, nearestIdx] = min(vecnorm(nodes - randPoint, 2, 2));
    nearestNode = nodes(nearestIdx, :);
    
    % Extend towards the random point
    direction = (randPoint - nearestNode) / norm(randPoint - nearestNode);
    newNode = nearestNode + maxStep * direction;
    
    % Collision check (assume no obstacles for simplicity)
    if newNode(1) >= mapSize(1) && newNode(1) <= mapSize(2) && ...
       newNode(2) >= mapSize(3) && newNode(2) <= mapSize(4)
        nodes = [nodes; newNode];
        edges = [edges; nearestIdx, size(nodes, 1)];
    end
    
    % Plot current state
    plot(nodes(:,1), nodes(:,2), 'bo'); % Plot nodes
    hold on;
    plot([nodes(edges(:,1),1), nodes(edges(:,2),1)]', ...
         [nodes(edges(:,1),2), nodes(edges(:,2),2)]', 'k-'); % Plot edges
    plot(goalPos(1), goalPos(2), 'ro', 'MarkerFaceColor', 'r'); % Plot goal
    pause(0.1);
end

% Final path plotting
plot([nodes(end,1), goalPos(1)], [nodes(end,2), goalPos(2)], 'r-', 'LineWidth', 2);
title('2D RRT Path Planning');
xlabel('X');
ylabel('Y');
grid on;

参考文献

❝

1. LaValle, S. M. (1998). Rapidly-Exploring Random Trees: A New Tool for Path Planning. Technical Report, Iowa State University.

2. Karaman, S., & Frazzoli, E. (2010). Incremental Sampling-Based Algorithms for Optimal Motion Planning. Robotics: Science and Systems VI.

3. Liu, J. (2024). Algorithms for Randomized Path Planning in Complex Environments. Springer.