🤵♂️ 个人主页:@艾派森的个人主页
✍🏻作者简介:Python学习者
🐋 希望大家多多支持,我们一起进步!😄
如果文章对你有帮助的话,
欢迎评论 💬点赞👍🏻 收藏 📂加关注+
目录
1.项目背景
2.项目简介
2.1分析目标
2.2数据集介绍
3.算法理论
4.实验过程
4.1数据探索
4.2因子分析
4.3 构建模型
5.总结
摘要
葡萄酒作为世界上最早的饮料酒之一,其品质和文化早已被人们所认可。据统计2021年,全球葡萄酒产量260亿升,较2020年下降了近1%,至此已连续3年略低于10年平均水平。由于我国本土葡萄酒长期以来受到进口葡萄酒的冲击及2020年疫情期间节日聚会、家庭餐会均被取消,餐饮业完全停滞,导致葡萄酒的需求短期内大幅下降。2020年我国葡萄酒行业市场规模下滑至498.2亿元,2021年小幅度上涨至510.8亿元。预计2022年我国葡萄酒行业市场规模将进一步上升至587.2亿元。本次实验使用葡萄酒数据集进行因子分析,最后构建葡萄酒分类模型,用来对葡萄酒的分类。
1.项目背景
作为世界上最早的饮料酒之一,葡萄酒的发展与西方文明紧密相关。根据酿造历史和生产工艺,葡萄酒生产国被划分为传统酿造工艺为代表的“旧世界”,包括法国、意大利、西班牙、德国等,以及以现代酿造技术为代表的“新世界”,包括美国、澳大利亚、新西兰、智利、阿根廷和南非等。据统计2021年,全球葡萄酒产量260亿升,较2020年下降了近1%,至此已连续3年略低于10年平均水平。受霜冻影响,欧盟的葡萄酒产量153.7亿升,较2020年下降8%。这主要是由于2021年4月份霜冻导致法国葡萄酒产量大幅下降。意大利(50.2亿升,增2%)、法国(37.6亿升,降19%)、西班牙(35.3亿升,降14%)三个国家占全球葡萄酒产量的47%。
由于我国本土葡萄酒长期以来受到进口葡萄酒的冲击及2020年疫情期间节日聚会、家庭餐会均被取消,餐饮业完全停滞,导致葡萄酒的需求短期内大幅下降。2020年我国葡萄酒行业市场规模下滑至498.2亿元,2021年小幅度上涨至510.8亿元。预计2022年我国葡萄酒行业市场规模将进一步上升至587.2亿元。
葡萄酒行业产业链上游参与主体为原材料及相关设备,主要包括葡萄、淀粉、酵母、食品添加剂、包装材料和酿造设备等;中游为葡萄酒行业,主要有白葡萄酒、红葡萄酒和桃红葡萄酒三大类;下游为各类消费渠道,最后到达终端消费者。近年来,随着葡萄酒产业链延伸,出现了各类“葡萄酒+”产业的新型模式,如“葡萄酒+旅游”、“葡萄酒+科技”等。
随着我国全面步入小康社会,人们的生活水平不断提高,消费市场持续升级,为具有一定品牌溢价能力的中高端葡萄酒带来较大发展空间。经过近几年的努力,中国葡萄酒的品质与风味已经赢得广大消费者认可,这也为中国葡萄酒搏击中高端葡萄酒市场奠定了基础。综合看来,中高端葡萄酒将是2022年乃至中国葡萄酒产业更长时间的发展热点。
近年来,随着民族、文化自信等因素助力国产品牌崛起,中国葡萄酒品质与世界接轨,屡次斩获国际性大奖,越来越多的消费者和经销商关注并选择国产葡萄酒。国产葡萄酒收割存量市场持续加速,“国产”替代“进口”的趋势明显。同时,伴随着进口葡萄酒的持续下滑,国产葡萄酒的替代效应越发明显。预计2022年,我国葡萄酒行业国产替代的速度将进一步加快。
2.项目简介
2.1分析目标
通过研究葡萄酒数据集做出以下分析:
①使用因子分析对数据进行因子提取
②构建葡萄酒分类模型
2.2数据集介绍
wine样本数据集中是double类型的178 * 14矩阵包括了三种酒中13种不同成分的数量。文件中,每行代表一种酒的样本,共有178个样本,一共有14列,其中,第一个属性是类标识符,分别是1/2/3来表示,代表葡萄酒的三个分类。后面的13列为每个样本的对应属性的样本值。剩余的13个属性是,酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调、稀释葡萄酒的OD280/OD315、脯氨酸。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。具体属性描述如下:
| 属性 | 属性描述 |
| Label | 类别 |
| Alcohol | 酒精 |
| Malic acid | 苹果酸 |
| Ash | 灰 |
| Alkalinity of ash | 灰分的碱度 |
| Magnesium | 镁 |
| Total phenoids | 总酚 |
| Flavonoids | 黄酮类化合物 |
| Noflavanoid phenols | 非黄烷类酚类 |
| Proanthocyanins | 原花色素 |
| Color intensity | 颜色强度 |
| Hue | 色调 |
| 0D280/0315ofdiluted wines | 稀释葡萄酒的0D280/0315 |
| proline | 脯氨酸 |
3.算法理论
因子分析(Factor Analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。
例如,在企业形象或品牌形象的研究中,消费者可以通过一个由24个指标构成的评价体系评价百货商城的24个方面的优劣。但消费者主要关心三个方面,即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量找出反映商店环境、商店服务水平和商品价格的3个潜在的因子,对商店进行综合评价。这3个公共因子可以表示为:
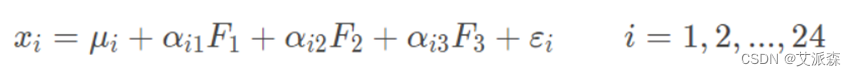
1.因子分析与主成分分析的区别
主成分分析仅仅是变量变换,而因子分析需要构造因子模型。
因子分析:潜在的假想变量和随机影响变量的线性组合表示原始变量。
主成分分析:原始变量的线性组合表示新的综合变量,即主成分。
因子分析数学模型
假设有P个变量X,有m个因子(m≤p),则因子分析的数学模型可以表示如下:
![]()
2.因子旋转
若因子分析中得出的各个因子有明确的含义,则因子分析的模型会更加易于解释和有实际意义。在因子分析中可以对因子载荷矩阵进行旋转,使每个变量仅在一个公共因子上有较大的载荷,而在其余的公共因子上的载荷比较小。通过旋转,因子可以有更加明确的含义。常用的一种方法是方差最大旋转。
3.因子得分及其计算
前面我们主要解决了用公共因子的线性组合来表示一组观测变量的有关问题。如果要使用这些因子做其他的研究,比如把得到的因子作为自变量来进行回归分析,对样本进行分类或评价,就需要计算每个个体在每个因子上的得分。
要计算因子得分,需要估计以下表达式:
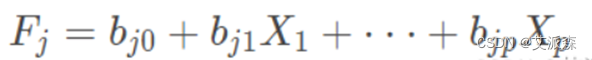
4.因子分析的步骤
因子分析解决的3个基本问题:
因子载荷阵A的估计
当因子难以得到合理的解释时,对因子载荷阵进行正交变换,即因子旋转。对因子的实际意义做出合理的解释。
给出每个变量(或样品)关于m个公共因子的得分,通常表示为原始变量的线性组合,即因子得分函数。对公共因子做出估计。
因子分析的步骤:
(1)根据问题选取原始变量。
(2)求其相关阵R,探讨其相关性,
(3)从R求解初始公共因子F及其因子载荷矩阵A(主成分法)。
(4)因子旋转,分析因子的含义。
(5)计算因子得分函数。
(6)根据因子得分值进行进一步分析(例如综合评价)。
5.因子分析与主成分分析的区别和联系
(1)因子分析、主成分分析都是重要的降维方法(即数据简化技术),因子分析可以看作主成分分析的推广和发展。
(2)主成分分析不能作为一个模型来描述,它只能作为一般的变量变换,主成分是可观测的原始变量的线性组合。因子分析需要构造因子模型,公共因子是潜在的不可观测的变量,一般不能表示为原始变量的线性组合。
(3)因子分析是用潜在的、不可观测的变量和随机变量的线性组合来表示原始变量,即通过这样的分解来分析原始变量的协方差结构(相依关系)。
4.实验过程
4.1数据探索
首先使用SPSS导入葡萄酒数据集
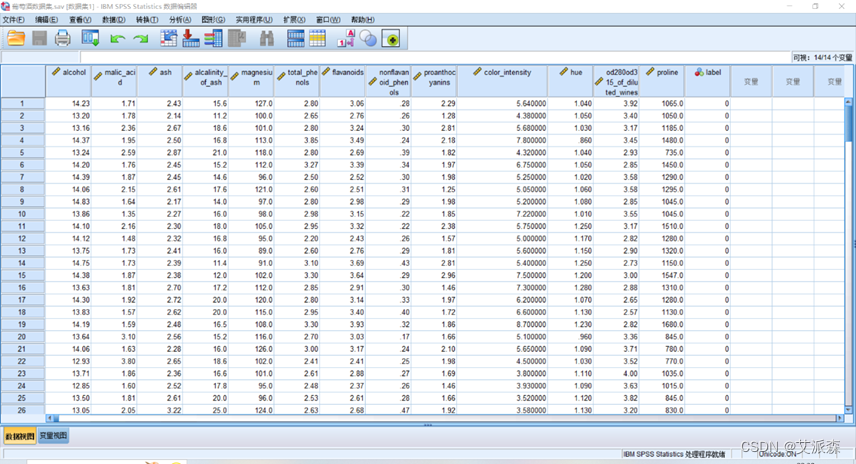
查看数据描述性统计
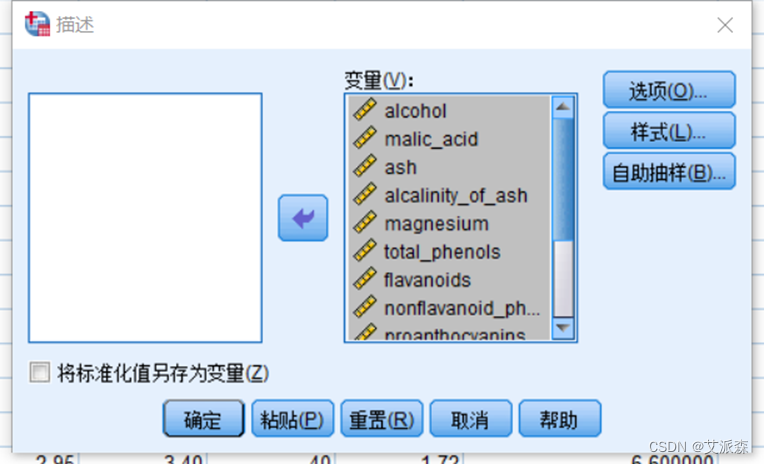
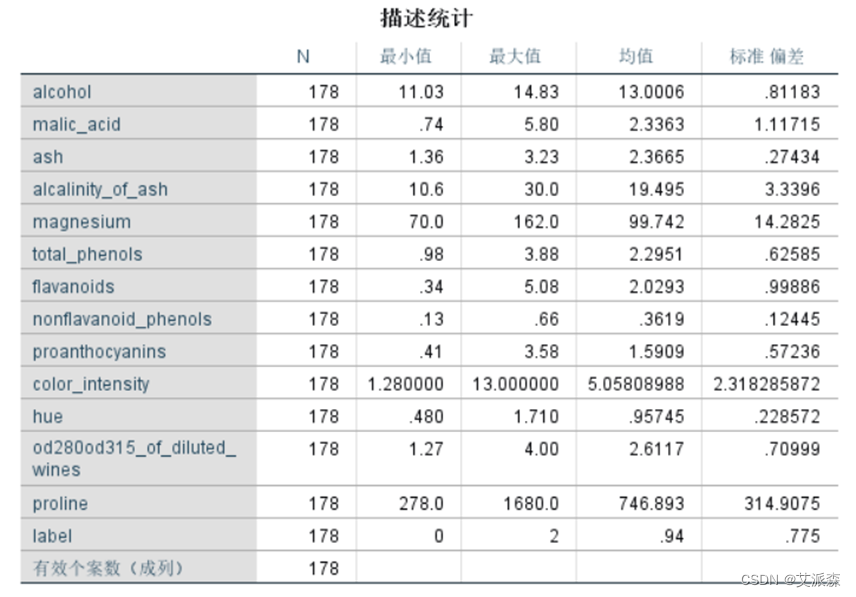
从描述性统计结果中可看出各个变量的个案数、最大最小值、均值、标准偏差等信息。
查看不同类别的酒精alcohol分布
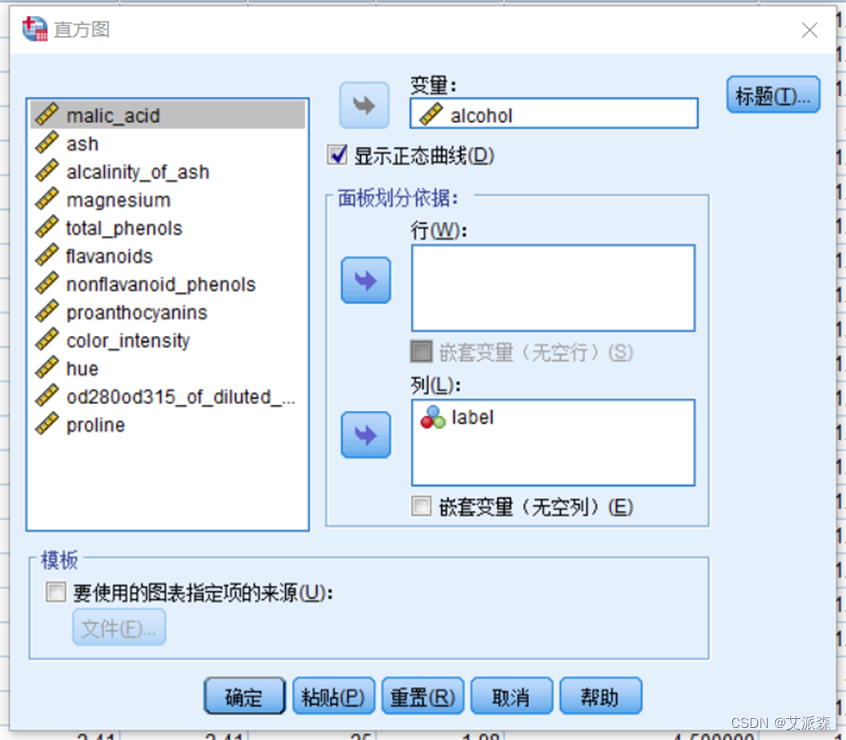
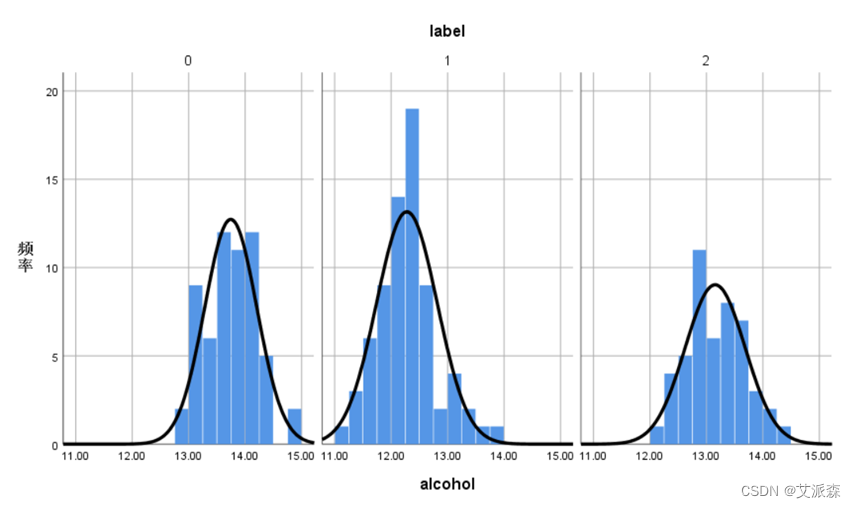
从结果可看出不同类别的酒精含量都近似服从正态分布。
查看不同类别的数目
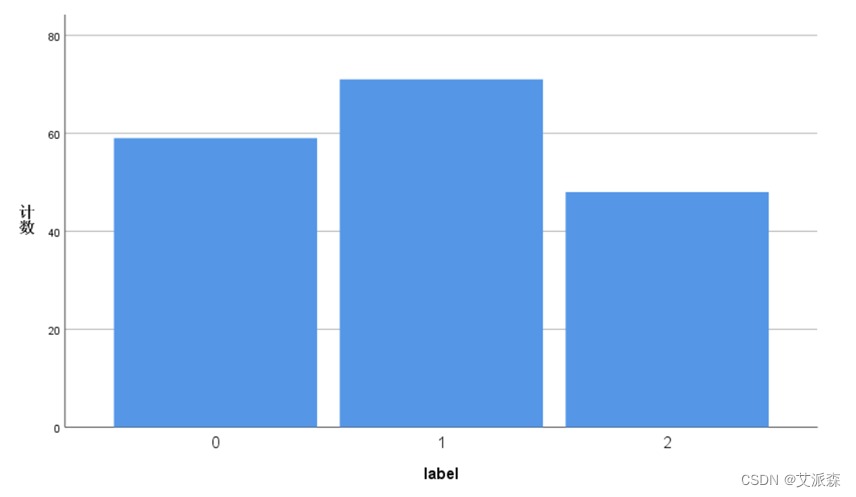
从图中可看出label为1的数量最多,2的最少。
4.2因子分析
1.选择变量
2.勾选描述中的选项
3.在提取中勾选碎石图
4.在旋转中勾选选项
5.勾选因子得分中的选项
6.勾选选项
7.结果如下
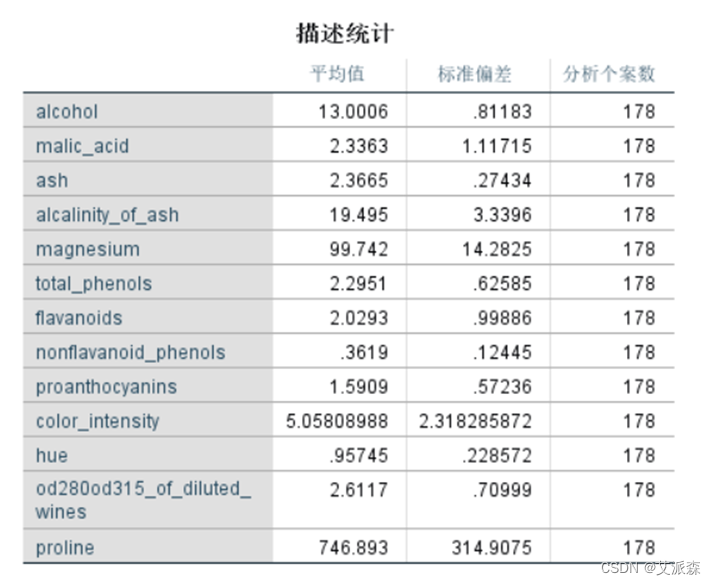
从描述统计中可以看到各个变量的平均值,标准偏差及分析个案数。
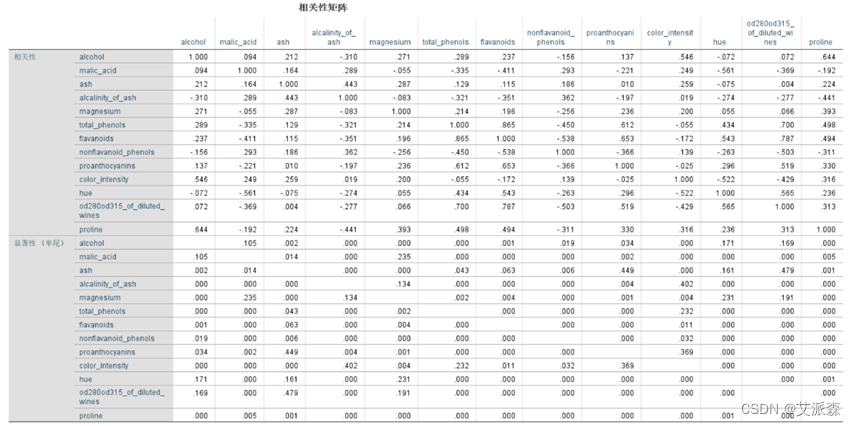
从相关性矩阵中可以看到,每个变量与每个变量之间的相关性高。从显著性值可以看每个变量与每个变量之间是否显著相关。从表中发现大多数概率P值都是小于 0.05的,说明大多数变量之间相关性显著。

从结果中看出,KMO值为0.779,巴特勒球形检验P值为0,两个指标都符合因子分析的前提,所以此数据适合做因子分析。
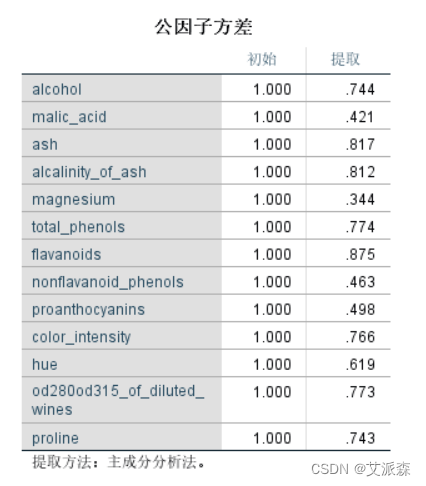
从公因子方差表中可以看到提取值都比较高,表明变量中大部分信息能被因子所提取,说明因子分析结果有效。
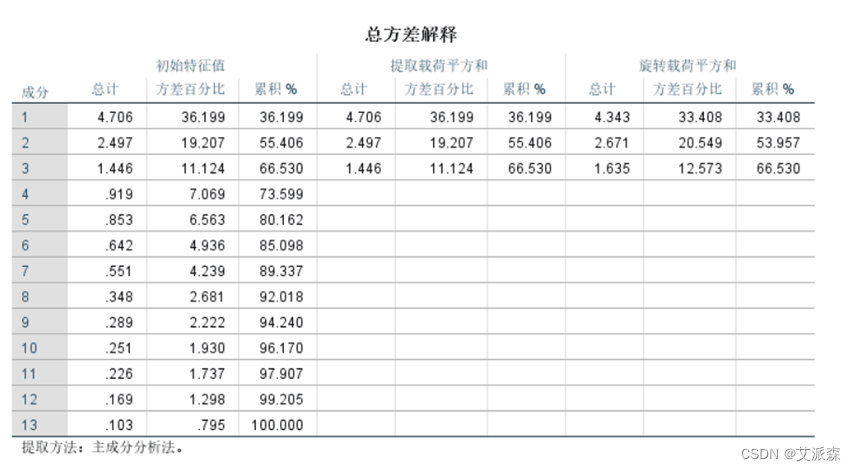
第一个成分的初始特征值为4.706能解释的方差比例为36.199%,第二个特征值为2.497,能解释的方差比例为19.207%,第三个特征值为1.446,能解释的方差比例为11.124%。其余成分都小于1,说明这几个成分的解释力度还不如直接引入原变量大。这些变量只需要提取出前三个成分即可。
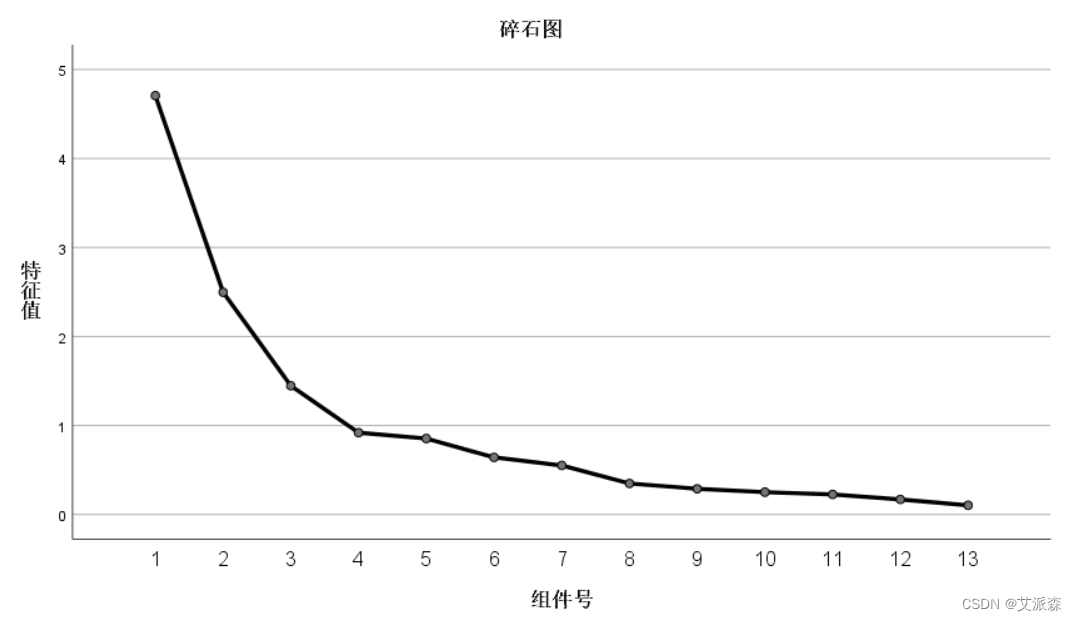
碎石图中,从第三个成分以后的特征值就降得非常低。第三个成分就是这一图形的“拐点”。在这一实例中,只需要提取三个主要成分就行了。
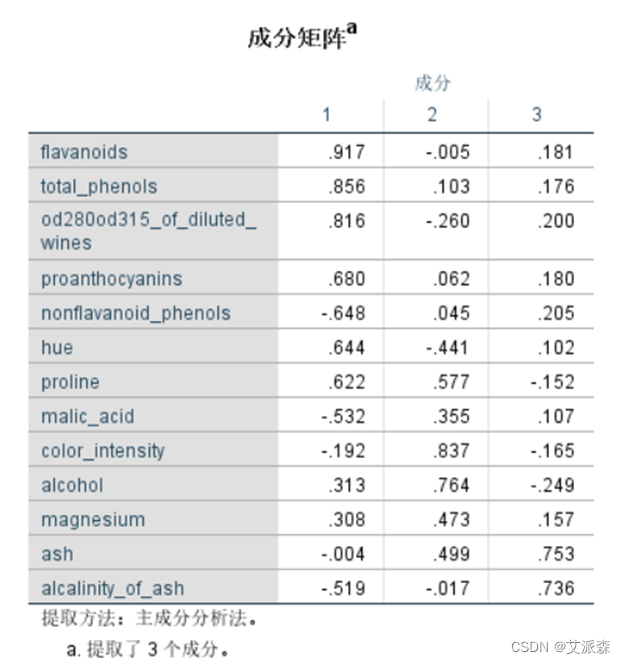
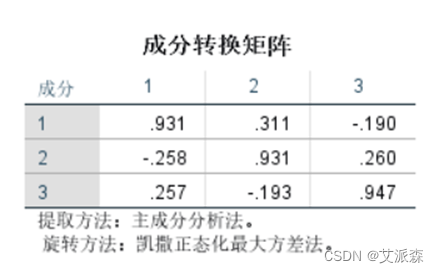
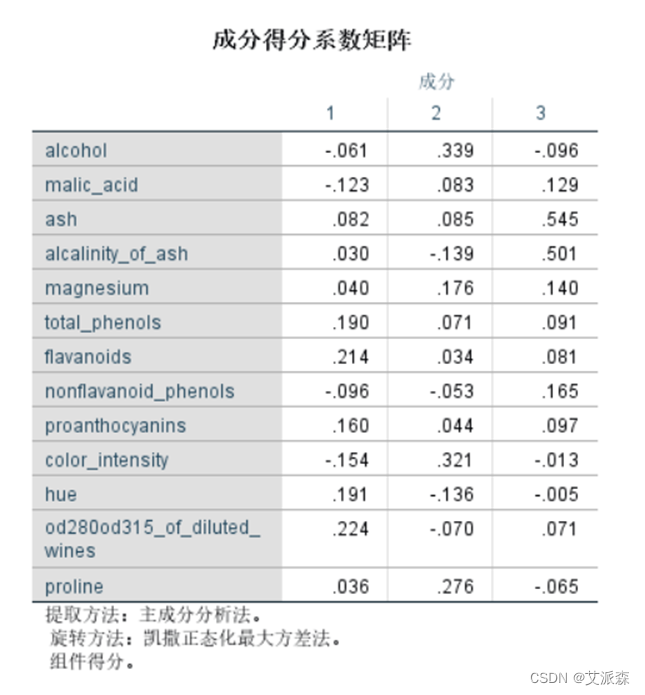
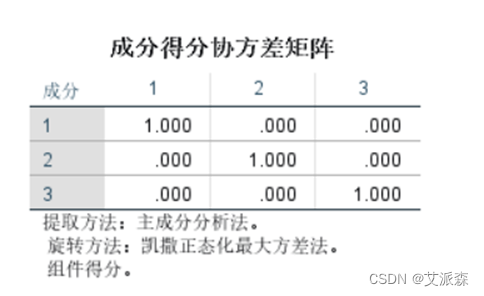
表中列出未使用旋转方法时使用因子能解释的各个变量的比例。
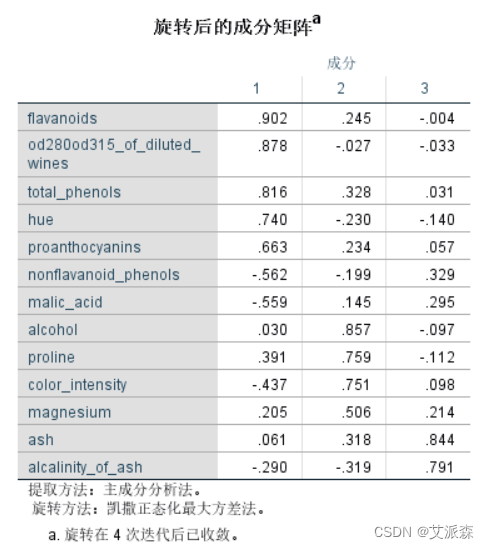
表中列出了使用旋转方法后因子能解释的各个变量的比例。和上面未旋转对比可以看出,旋转后,原先较大的比例值仍然大,较小的比例则变得更小。

4.3 构建模型
这里我们使用SPSS构建决策树分类模型
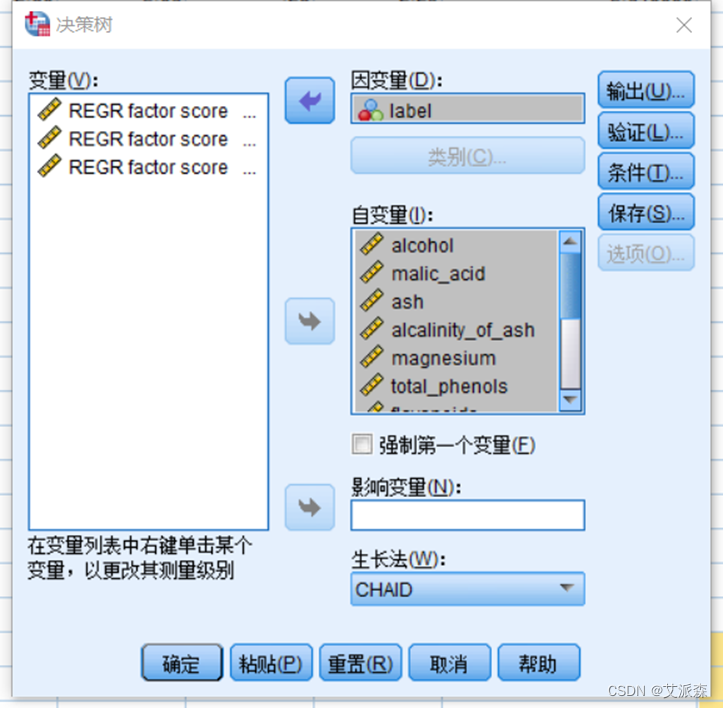
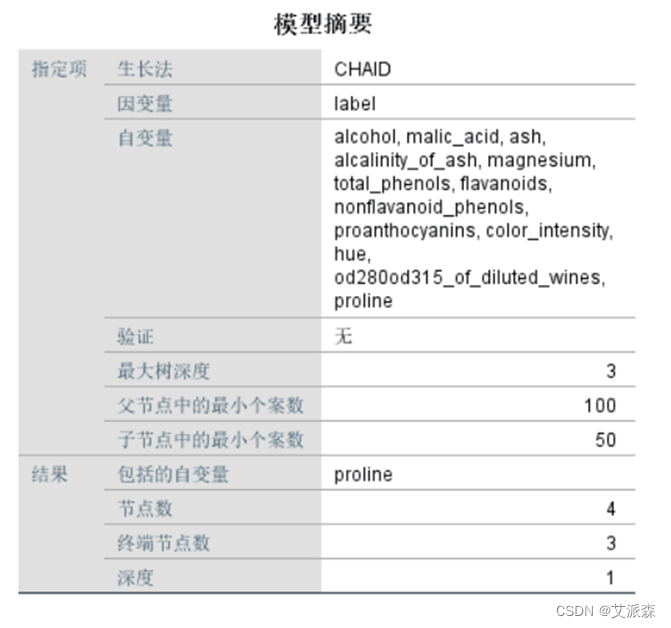

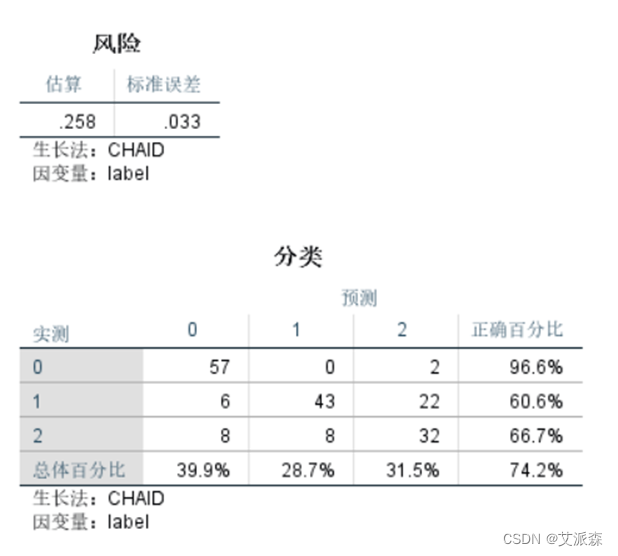
从模型分类结果来看,模型在0分类上正确率为96.6%,在1分类上正确率为60.6%,在2分类上正确率为66.7%,最后综合的准确率为74.2%。
前面我们使用的是原始自变量,现在我们使用通过因子分析提取的3个主因子作为自变量重新训练模型
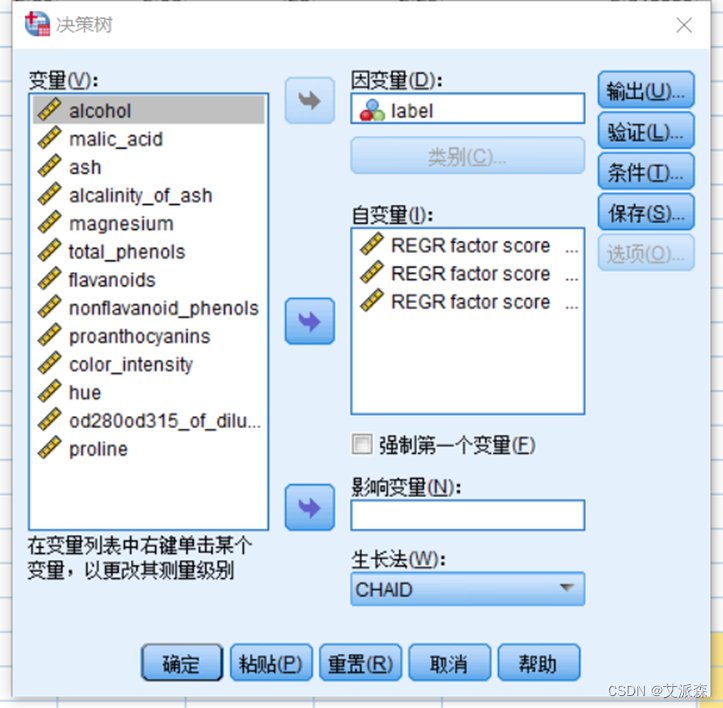
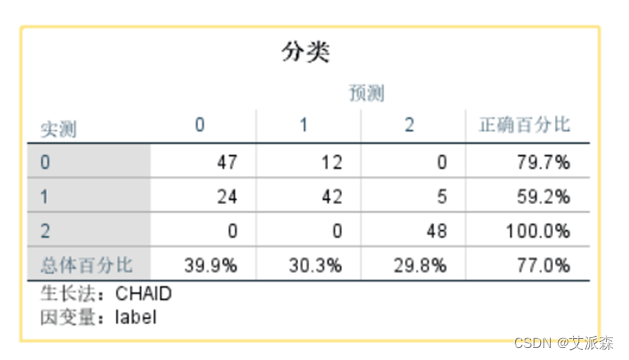
可以看出使用因子分析提取的3个主因子作为自变量训练模型,使得模型的综合准确率提高了3%.
5.总结
本次实验对葡萄酒数据进行了因子分析,将13维的数据提取了3个主要因子,最后通过构建决策树分类模型得出的模型准确率为0.77,相比于没有经过因子分析处理的数据构建的模型而言,经过处理后的数据构建的模型准确率提高了3%,说明本次因子分析是有效果的,最后构建的模型效果也很不错。
资料获取,更多粉丝福利,关注下方公众号获取