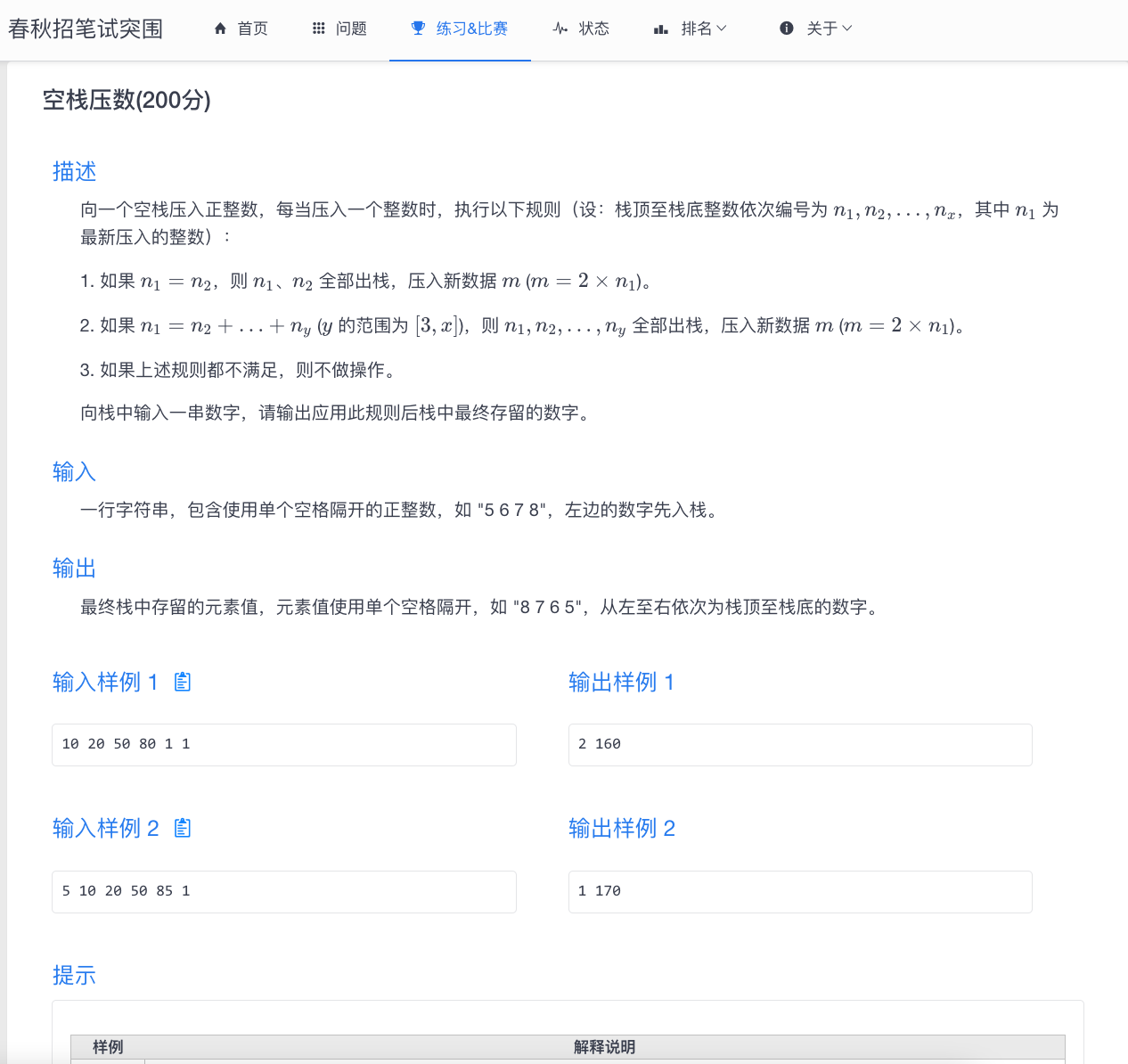
1、a数组可能存在重复元素
      去重 + 排序
2、如何算出 x 离散化后的值
      二分 

1、add 和 query 记录每次填入的两个数
2、将位置 x 和每次询问的两个数 l 和 r 添加到 alls 进行排序去重
3、通过Collections.binarySearch映射（一定能找到，不用判断）
        在 add 中，找位置 x 映射的下标，然后加1，使数组a[]从下标1开始，便于前缀和s[]
        在 query 中，找 l 和 r 映射的下标，通过前缀和数组求出结果

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
import java.util.stream.Collectors;

public class Main {

    private static final int N = 300000;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        List<Integer> alls = new ArrayList<>();
        int[] a = new int[N];
        int[] s = new int[N];
        List<int[]> add = new ArrayList<>();
        List<int[]> query = new ArrayList<>();

        for (int i = 0; i < n; i++) {
            int x = in.nextInt();
            int c = in.nextInt();
            add.add(new int[]{x, c});
            alls.add(x);
        }

        for (int i = 0; i < m; i++) {
            int l = in.nextInt();
            int r = in.nextInt();
            query.add(new int[]{l, r});
            alls.add(l);
            alls.add(r);
        }

        // 去重 + 排序
        List<Integer> distinctSorterAlls = alls.stream().distinct().sorted()
                .collect(Collectors.toList());

        // 离散化映射，把离散化的下标映射到连续的数组下标 + 1，让数组从下标1开始
        for (int[] item : add) {
            int index = Collections.binarySearch(distinctSorterAlls, item[0]);
                a[index + 1] += item[1];
        }

        // 前缀和
        for (int i = 1; i <= distinctSorterAlls.size(); i++)
            s[i] = s[i - 1] + a[i];

        // 离散化映射，把离散化的下标映射到连续的数组下标 + 1
        for (int[] item : query) {
            int l = Collections.binarySearch(distinctSorterAlls, item[0]);
            int r = Collections.binarySearch(distinctSorterAlls, item[1]);
            System.out.println(s[r + 1] - s[l]);
        }
    }
}

关于Collections.binarySearch
前提：有序不重复
1、提供插入点：
    返回 -(插入点 + 1) 可以帮助确定目标元素在排序列表中的位置。如果目标元素不存在，你可以立即知道它应该插入在哪里，而不是只知道它不在列表中。
2、处理插入操作：
    使用 -(插入点 + 1) 结果，能够方便地进行插入操作。这对于需要在查找的同时执行插入的场景尤其有用。