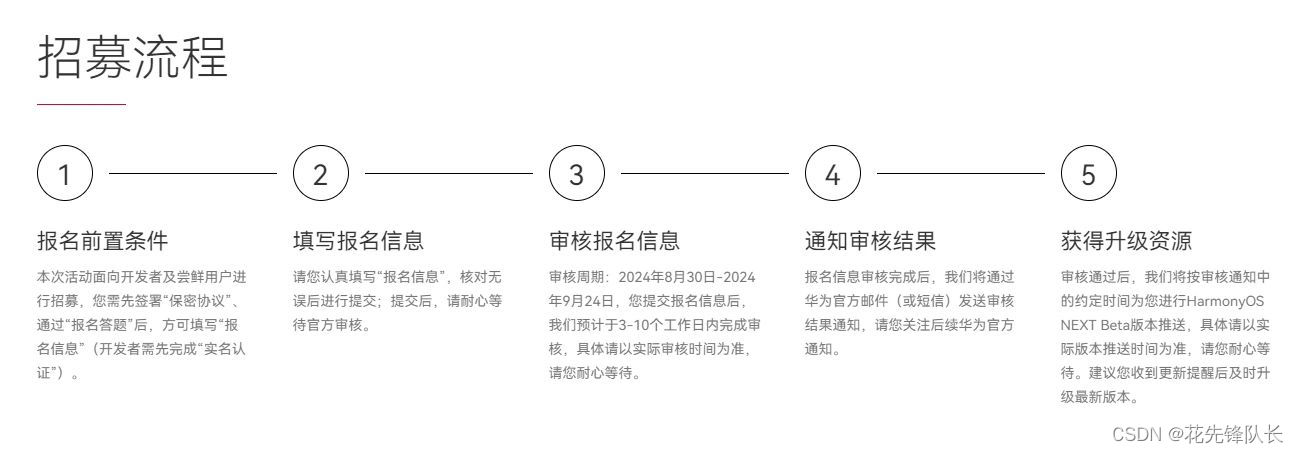
1. Dijkstra

1.1 原理与步骤

步骤：

1. 选取距离源点最近且未被访问过的节点
2. 标记该节点为已访问
3. 更新未访问节点到源点的距离

1.2 代码实现

以KamaCoder47题为例
题目：47. 参加科学大会（第六期模拟笔试） (kamacoder.com)

class Program
{
    public static void Main(string[] args)
    {
        //处理输入
        string[] dimensions = Console.ReadLine().Split();
        int n = int.Parse(dimensions[0]);
        int m = int.Parse(dimensions[1]);
        //  visited & minDist & graph
        bool[] visited = new bool[n + 1];
        int[] minDist = new int[n + 1];
        int[][] graph = new int[n + 1][];
        for (int i = 0; i <= n; i++)
        {
            graph[i] = new int[n + 1];
            for (int j = 0; j <= n; j++)
            {
                graph[i][j] = int.MaxValue;
            }
        }
        //  填充
        for (int i = 0; i <= n; i++)
        {
            visited[i] = false;
            if (i == 1) minDist[i] = 0;
            else minDist[i] = int.MaxValue;
        }
        for (int i = 0; i < m; i++)
        {
            string[] edges = Console.ReadLine().Split();
            int start = int.Parse(edges[0]);
            int end = int.Parse(edges[1]);
            int weight = int.Parse(edges[2]);
            graph[start][end] = weight;
        }
        //
        int result = Dj(graph, n, visited, minDist);
        Console.WriteLine(result);
    }

    public static int Dj(int[][] graph, int n, bool[] visited, int[] minDist)
    {
        for (int count = 1; count < n + 1; count++)
        {
            //find min node
            int mindist = int.MaxValue;
            int minnode = 0;
            for (int i = 1; i < n + 1; i++)
            {
                if (visited[i] == false)
                {
                    if (minDist[i] < mindist)
                    {
                        minnode = i;
                        mindist = minDist[i];
                    }
                }
            }
            //update visited
            visited[minnode] = true;
            //update minDist
            for (int i = 1; i < n + 1; i++)
            {
                if (graph[minnode][i] != int.MaxValue)
                {
                    minDist[i] = Math.Min(graph[minnode][i] + mindist, minDist[i]);
                }
            }
            Console.WriteLine(string.Join(" ", minDist));
        }

        return minDist[n] == int.MaxValue ? -1 : minDist[n];
    }
}

1.3 堆优化

2. Bellman_ford

2.1 原理与步骤

2.2 代码实现

class Program
{
    public static void Main(string[] args)
    {
        //处理输入
        string[] dimensions = Console.ReadLine().Split();
        int n = int.Parse(dimensions[0]);
        int m = int.Parse(dimensions[1]);
        //minDist
        int[] minDist = new int[n + 1];
        for (int i = 0; i <= n; i++)
        {
            minDist[i] = i == 1 ? 0 : int.MaxValue;
        }
        //edges
        int[][] edges = new int[m][];
        for (int i = 0; i < m; i++)
        {
            edges[i] = new int[3];
            string[] edge = Console.ReadLine().Split();
            edges[i][0] = int.Parse(edge[0]);
            edges[i][1] = int.Parse(edge[1]);
            edges[i][2] = int.Parse(edge[2]);
        }

        //BF
        if (BF(edges, minDist, n - 1))
        {
            Console.WriteLine(minDist[n]);
        }
        else
        {
            Console.WriteLine("unconnected");
        }
    }

    public static bool BF(int[][] edges, int[] minDist, int n)
    {
        bool isUpdate = true;
        int count = 1;
        while (count <= n && isUpdate == true)
        {
            count++;
            isUpdate = false;

            for (int i = 0; i < edges.Length; i++)
            {
                int start = edges[i][0];
                int end = edges[i][1];
                int weight = edges[i][2];
                if (minDist[start] != int.MaxValue)
                {
                    int dist = minDist[start] + weight;
                    if (dist < minDist[end])
                    {
                        minDist[end] = dist;
                        isUpdate = true;
                    }
                }
            }
        }

        return !isUpdate;
    }
}

2.3 队列优化

2.4 应用场景