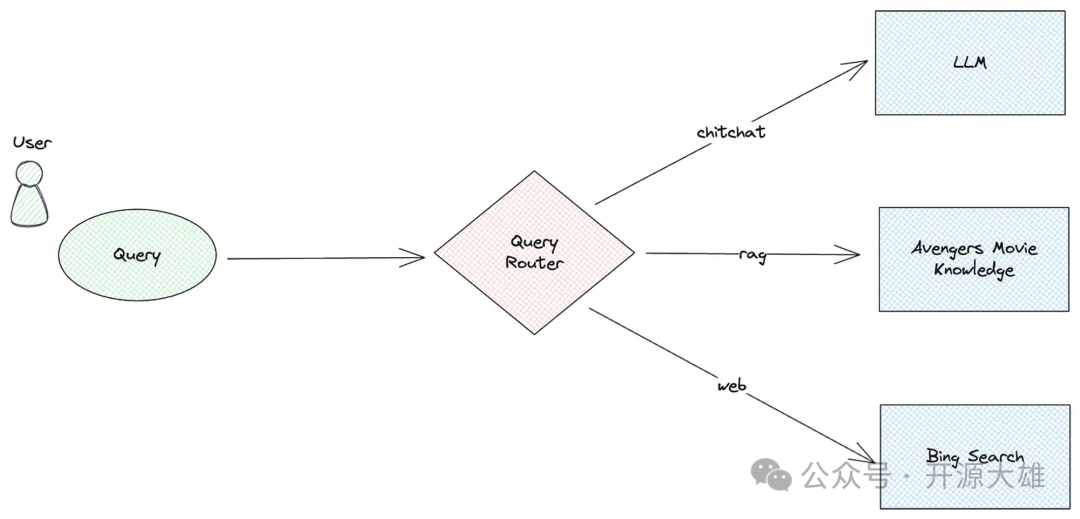
聚类属于无监督学习算法。下面讲解聚类中最常用的划分聚类方法，并对其中最具有代表性的 K-Means 算法进行介绍。

• 划分聚类介绍
• K-Means 聚类方法
• 中心点移动过程可视化
• K-Means++ 算法实现

划分聚类介绍

划分聚类，通过划分的方式将数据集划分为多个不重叠的子集（簇），每一个子集作为一个聚类（类别）。

在划分的过程中，首先由用户确定划分子集的个数 $k$，然后随机选定 $k$ 个点作为每一个子集的中心点，接下来通过迭代的方式：计算数据集中每个点与各个中心点之间的距离，更新中心点的位置；最终将数据集划分为 $k$ 个子集，即将数据划分为 $k$ 类。

而评估划分的好坏标准就是：保证同一划分的样本之间的差异尽可能的小，且不同划分中的样本差异尽可能的大。

K-Means 聚类方法

在划分聚类中，K-Means 是最具有代表性的算法，下面用图片的方式演示 K-Means 的基本算法流程。希望大家能通过简单的图文演示，对 K-Means 方法的原理过程产生大致的印象。

对于未聚类数据集，首先随机初始化 K 个（代表拟聚类簇个数）中心点，如图红色五角星所示。

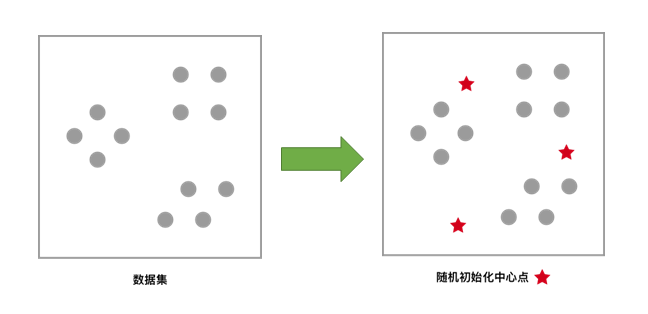
每一个样本按照距离自身最近的中心点进行聚类，等效于通过两中心点连线的中垂线划分区域。

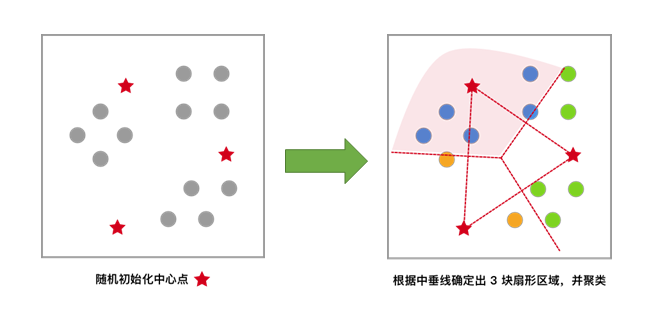
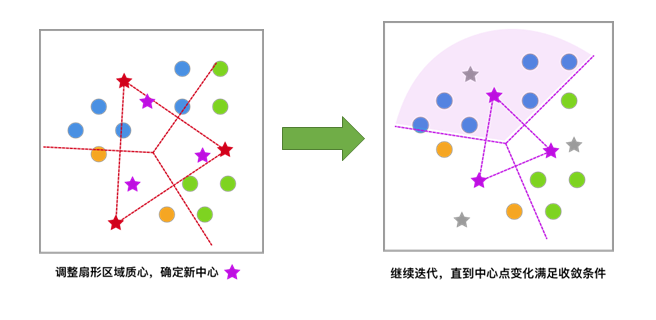
依据上次聚类结果，移动中心点到个簇的质心位置，并将此质心作为新的中心点

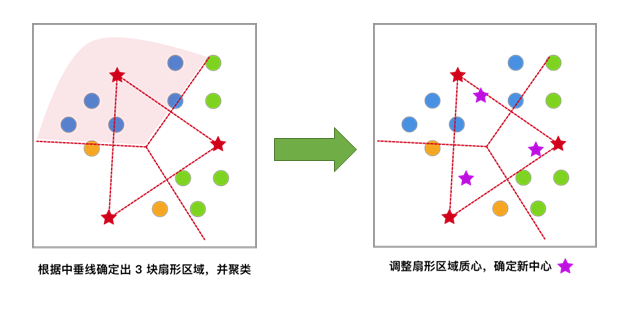
反复迭代，直至中心点的变化满足收敛条件（变化很小或几乎不变化），最终得到聚类结果。

用python实现聚类

生成示例数据

首先通过 scikit-learn 模块的 make_blobs() 函数生成本次实验所需的示例数据。该方法可以按照我们的要求，用来创建类似于“blobs”（团簇）的分布，通常用于聚类分析的示例

data,label = sklearn.datasets.make_blobs(n_samples=100,n_features=2,centers=3,center_box=(-10.0,10.0),random_state=None)   

参数为：

• n_samples：表示生成数据总个数,默认为 100 个。
• n_features：表示每一个样本的特征个数，默认为 2 个。
• centers：表示中心点的个数，默认为 3 个。
• center_box：表示每一个中心的边界,默认为 -10.0到10.0。
• random_state：表示生成数据的随机数种子。

返回值为：

• data：表示数据信息。
• label：表示数据类别。

根据上面函数，在 0.0 到 10.0 上生成 200 条数据，大致包含 3 个中心。这里的数据仅用于演示聚类效果，数据标签不是必须的，在生成数据时赋值给 _。

from sklearn.datasets import make_blobs

# 构造示例数据
blobs, _ = make_blobs(n_samples=200, centers=3, random_state=18)
blobs[:10]  # 打印出前 10 条数据的信息

array([[ 8.28390539,  4.98011149],
       [ 7.05638504,  7.00948082],
       [ 7.43101466, -6.56941148],
       [ 8.20192526, -6.4442691 ],
       [ 3.15614247,  0.46193832],
       [ 7.7037692 ,  6.14317389],
       [ 5.62705611, -0.35067953],
       [ 7.53828533, -4.86595492],
       [ 8.649291  ,  3.98488194],
       [ 7.91651636,  4.54935348]])

绘制数据分布

import matplotlib.pyplot as plt
%matplotlib inline

plt.scatter(blobs[:, 0], blobs[:, 1], s=20)  # 数据展示

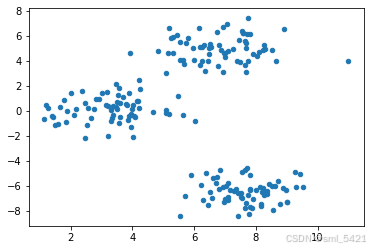
随机初始化中心点

当我们得到数据时，依照划分聚类方法的思想，首先需要随机选取 $k$ 个点作为每一个子集的中心点。从图像中，通过肉眼很容易的发现该数据集有 3 个子集。接下来，用 NumPy 模块随机生成 3 个中心点，为了更方便展示，这里我们加入了随机数种子以便每一次运行结果相同。

import numpy as np


def random_k(k, data):
    """
    参数:
    k -- 中心点个数
    data -- 数据集

    返回:
    init_centers -- 初始化中心点
    """
    # 初始化中心点
    prng = np.random.RandomState(1)  # 定义随机种子，只要使用相同的种子值，无论何时运行代码，生成的随机数序列都将是相同的。这使得可以重现实验结果或调试代码。
    num_feature = np.shape(data)[1]
    # 初始化从标准正态分布返回的一组随机数，为了更加贴近数据集这里乘了一个 5
    init_centers = prng.randn(k, num_feature)*5
    return init_centers


init_centers = random_k(3, blobs)
init_centers

array([[  8.12172682,  -3.05878207],
       [ -2.64085876,  -5.36484311],
       [  4.32703815, -11.50769348]])

在随机生成好中心点之后，将其在图像中表示出来，这里同样使用红色五角星表示。

# 初始中心点展示
plt.scatter(blobs[:, 0], blobs[:, 1], s=20)
plt.scatter(init_centers[:, 0], init_centers[:, 1], s=100, marker='*', c="r")

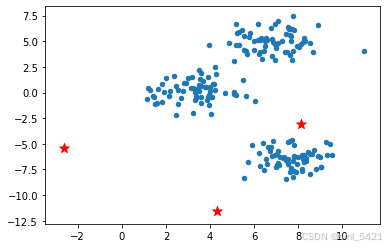
计算样本与中心点的距离

为了找到最合适的中心点位置，需要计算每一个样本和中心点的距离，从而根据距离更新中心点位置。这里采用欧几里得距离（欧式距离）。

欧氏距离公式如下：
$$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}\text{\hspace{1em}(1)}$$
python代码如下：

def d_euc(x, y):
    """
    参数:
    x -- 数据 a
    y -- 数据 b

    返回:
    d -- 数据 a 和 b 的欧氏距离
    """
    # 计算欧氏距离
    d = np.sqrt(np.sum(np.square(x - y)))
    return d

更新聚类中心

通过优化一个目标函数，评估聚类算法的质量。

在聚类算法中，常常使用误差的平方和 SSE（Sum of squared errors）作为度量聚类效果的标准，当 SSE 越小表示聚类效果越好。其中 SSE 表示为：

$$SSE(C)=\sum _{k=1}^K{x}_i\in C_k$$