代码随想录Day 29|leetcode题目：134.加油站、135.分发糖果、860.柠檬水找零、406.根据身高重建队列

提示：DDU，供自己复习使用。欢迎大家前来讨论~

文章目录

第八章贪心算法 part03
二、题目
题目一：134. 加油站
解题思路：
暴力方法
贪心算法（方法一）
贪心算法（方法二）

题目二：135. 分发糖果
解题思路：

题目三：860.柠檬水找零
解题思路：

题目四：406.根据身高重建队列
解题思路

总结

第八章贪心算法 part03

贪心算法

二、题目

题目一：134. 加油站

134. 加油站

解题思路：

暴力方法

暴力的方法很明显就是O(n^2)的，遍历每一个加油站为起点的情况，模拟一圈。

如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个起点是ok的。

暴力的方法思路比较简单，但代码写起来也不是很容易，关键是要模拟跑一圈的过程。

for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历，要善于使用while！

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); i++) {
            int rest = gas[i] - cost[i]; // 记录剩余油量
            int index = (i + 1) % cost.size();
            while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈（如果有rest==0，那么答案就不唯一了）
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            // 如果以i为起点跑一圈，剩余油量>=0，返回该起始位置
            if (rest >= 0 && index == i) return i;
        }
        return -1;
    }
};

时间复杂度：O(n^2)
空间复杂度：O(1)

贪心算法（方法一）

直接从全局进行贪心选择，情况如下：

情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的
情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。
情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能把这个负数填平，能把这个负数填平的节点就是出发节点。

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int min = INT_MAX; // 从起点出发，油箱里的油量最小值
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            if (curSum < min) {
                min = curSum;
            }
        }
        if (curSum < 0) return -1;  // 情况1
        if (min >= 0) return 0;     // 情况2
                                    // 情况3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest;
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

时间复杂度: O(n)
空间复杂度: O(1)

贪心算法（方法二）

可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明各个站点的加油站剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

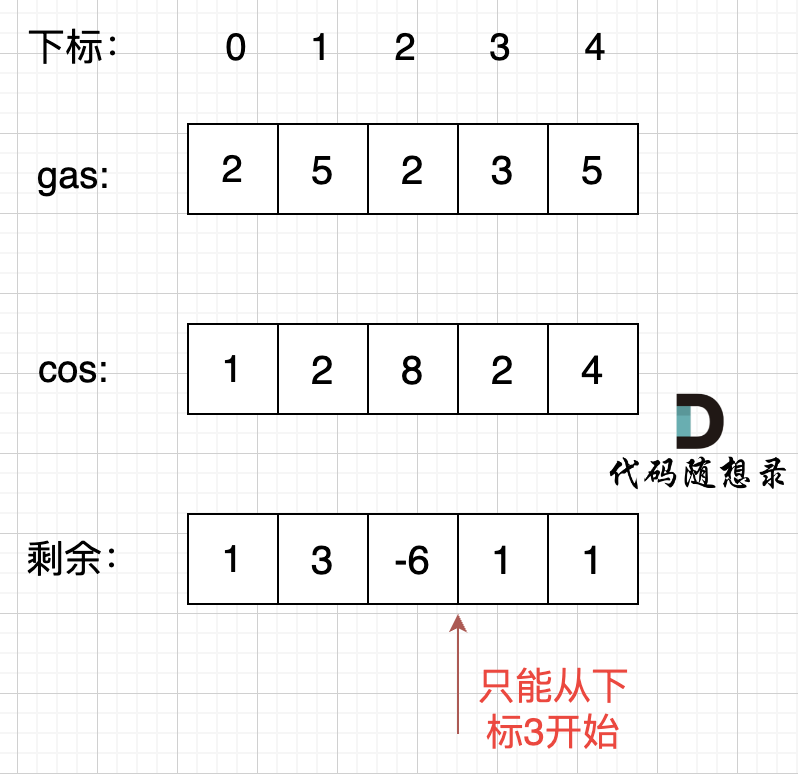
局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

局部最优可以推出全局最优，找不出反例，试试贪心！

C++代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0
                start = i + 1;  // 起始位置更新为i+1
                curSum = 0;     // curSum从0开始
            }
        }
        if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了
        return start;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

题目二：135. 分发糖果

135. 分发糖果

解题思路：

问题：需要根据孩子们的评分来分配糖果，确保评分高的孩子得到的糖果多于评分低的孩子。
确定策略：采用贪心算法，即在每一步选择当前最优的决策，不考虑其他可能的全局最优解。
初始化：为每个孩子分配至少一个糖果。
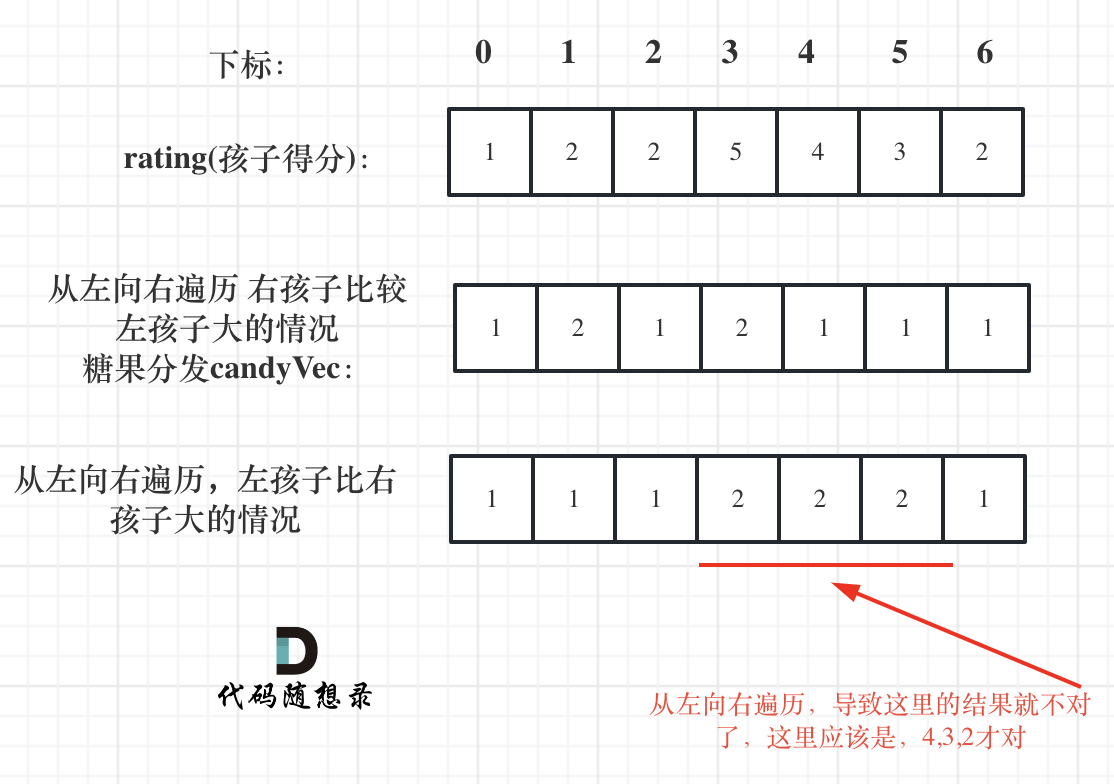
第一轮遍历（从前向后）：
- 从左到右遍历孩子们的评分。
- 如果当前孩子的评分高于他左边的孩子，那么他应该得到比左边孩子多至少一个糖果。
局部到全局：
- 通过确保每个评分更高的孩子在糖果数量上也更高，逐步构建全局最优解。
第二轮遍历（从后向前，可选）：
- 从右到左再次遍历孩子们的评分。
- 如果当前孩子的评分低于他右边的孩子，并且当前孩子的糖果数不比右边的孩子多，那么增加他的糖果数。
结束条件：完成两轮遍历后，得到的糖果分配方案即为最终解。

// 从前向后
for (int i = 1; i < ratings.size(); i++) {
    if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}

得到下图的列表：

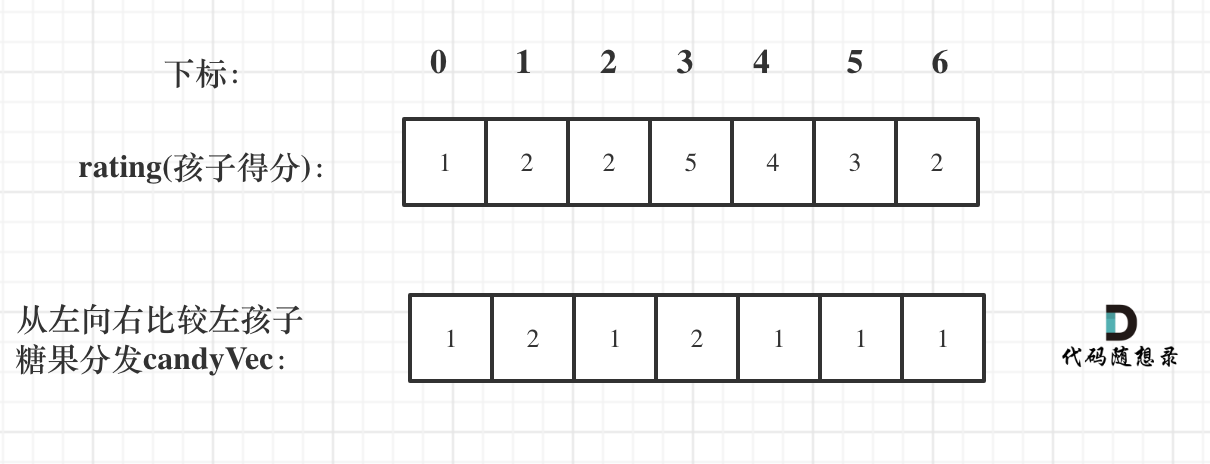
再确定左孩子大于右孩子的情况（从后向前遍历）

// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1] ) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

整体代码如下：

class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> candyVec(ratings.size(), 1);
        // 从前向后
        for (int i = 1; i < ratings.size(); i++) {
            if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
        }
        // 从后向前
        for (int i = ratings.size() - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1] ) {
                candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
            }
        }
        // 统计结果
        int result = 0;
        for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
        return result;
    }
};

时间复杂度: O(n)
空间复杂度: O(n)

题目三：860.柠檬水找零

860. 柠檬水找零

解题思路：

只需要维护三种金额的数量，5，10和20。

有如下三种情况：

情况一：账单是5，直接收下。
情况二：账单是10，消耗一个5，增加一个10
情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5

此时发现情况一，情况二，都是固定策略，都不用我们来做分析了，而唯一不确定的其实在情况三。

情况三看似简单，实则蕴含贪心策略，即优先使用美元10解决当前找零问题。

因为美元10只能给账单20找零，而美元5可以给账单10和账单20找零，美元5更万能！

局部最优可以推出全局最优，并找不出反例，那么就试试贪心算法！

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        int five = 0, ten = 0, twenty = 0;
        for (int bill : bills) {
            // 情况一
            if (bill == 5) five++;
            // 情况二
            if (bill == 10) {
                if (five <= 0) return false;
                ten++;
                five--;
            }
            // 情况三
            if (bill == 20) {
                // 优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着
                if (five > 0 && ten > 0) {
                    five--;
                    ten--;
                    twenty++; // 其实这行代码可以删了，因为记录20已经没有意义了，不会用20来找零
                } else if (five >= 3) {
                    five -= 3;
                    twenty++; // 同理，这行代码也可以删了
                } else return false;
            }
        }
        return true;
    }
};

时间复杂度: O(n)
空间复杂度: O(1)

小结：

咋眼一看好像很复杂，分析清楚之后，会发现逻辑其实非常固定。

这道题目可以告诉大家，遇到感觉没有思路的题目，可以静下心来把能遇到的情况分析一下，只要分析到具体情况了，一下子就豁然开朗了。

如果一直陷入想从整体上寻找找零方案，就会把自己陷进去，各种情况一交叉，只会越想越复杂了。

题目四：406.根据身高重建队列

406. 根据身高重建队列

解题思路

本题有两个维度，h和k，看到这种题目一定要想如何确定一个维度，然后再按照另一个维度重新排列。
解题思路和135.分发糖果很类似。遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。

避免同时考虑两个维度：如果同时考虑两个维度（k和h），可能会导致无法同时满足两个条件，从而顾此失彼。
选择一个维度进行排序：在k和h两个维度中，选择先按身高h进行排序，且身高高的排在前面。这样做可以确定一个维度，即身高，确保前面的节点都比当前节点高。
排序策略：在身高相同的情况下，选择k值较小的节点排在前面，这样可以在确定身高维度的同时，尽可能地满足另一个维度的条件。

按照身高排序之后，优先按身高高的people的k来插入，后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。

所以在按照身高从大到小排序后：

局部最优：优先按身高高的people的k来插入。插入操作过后的people满足队列属性

全局最优：最后都做完插入操作，整个队列满足题目队列属性

局部最优可推出全局最优，找不出反例，那就试试贪心。

整体的插入步骤：

排序完的people： [[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]]

插入的过程：

插入[7,0]：[[7,0]]
插入[7,1]：[[7,0],[7,1]]
插入[6,1]：[[7,0],[6,1],[7,1]]
插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

此时就按照题目的要求完成了重新排列。

// 版本一
class Solution {
public:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        vector<vector<int>> que;
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1];
            que.insert(que.begin() + position, people[i]);
        }
        return que;
    }
};

时间复杂度：O( $nlog n + n^2$ )
空间复杂度：O(n)

动态数组的局限性：C++中的vector（动态数组）在插入元素时，如果当前容量不足以容纳新元素，就需要进行扩容操作。扩容通常涉及到申请一个更大的内存空间，并将现有数据复制到新的内存位置，这个过程是耗时的。

插入操作的效率问题：使用vector进行插入操作时，如果频繁触发扩容，那么单纯插入操作的时间复杂度可能达到O(n^2)，甚至在多次拷贝的情况下，性能损耗可能会更加严重。

改成链表之后，C++代码如下：

// 版本二
class Solution {
public:
    // 身高从大到小排（身高相同k小的站前面）
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        list<vector<int>> que; // list底层是链表实现，插入效率比vector高的多
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1]; // 插入到下标为position的位置
            std::list<vector<int>>::iterator it = que.begin();
            while (position--) { // 寻找在插入位置
                it++;
            }
            que.insert(it, people[i]);
        }
        return vector<vector<int>>(que.begin(), que.end());
    }
};