一:资本资产定价模型(CAPM)
资本资产定价模型(Capital Asset Pricing Model,简称CAPM)是金融学中一个重要的理论模型,用于估算一个投资的预期回报率,并确定投资的风险与预期回报之间的关系。
CAPM 的核心观点是,资产的预期回报率与无风险利率、资产的系统性风险(即贝塔系数,Beta)和市场的预期回报率有关。系统性风险是指资产收益与整个市场收益的相关性,非系统性风险则是特定于个别资产的风险,通常可以通过分散投资来消除。

无风险收益率、特定证券的贝塔值和市场组合的预期收益率是资本资产定价模型(CAPM)中的关键参数。这些参数通常通过以下方式获得:
-
无风险收益率:
- 通常以国债或政府债券的收益率作为无风险收益率的代表,因为这些债券被认为是几乎没有违约风险的。
- 可以从金融新闻网站、政府债券市场数据或金融数据库中获取。
-
特定证券的贝塔值:
- 贝塔值衡量证券相对于市场整体的波动性,它可以通过历史数据分析计算得出。
- 计算方法通常涉及回归分析,其中证券的历史收益率与市场组合(如大盘指数)的历史收益率进行比较。
- 贝塔值也可以从金融分析报告或金融数据库中获取。
-
市场组合的预期收益率:
- 市场组合的预期收益率通常是基于市场分析师的预测、经济指标、历史数据等综合得出的。
- 可以从金融分析师的报告、市场研究机构的预测或金融数据库中获取。
CAPM 的几个关键点:
- 风险与回报的关系:投资者为承担更高的风险而期望获得更高的回报。
- 系统性风险:CAPM 只关注系统性风险,因为它认为非系统性风险可以通过投资组合的分散化来消除。
- 市场组合:CAPM 假设投资者持有市场组合,即包含所有风险资产的组合,每个资产的权重与其市场价值成比例。
- 无风险利率:投资者可以无风险地投资于政府债券等工具,获得无风险利率。
CAPM 在实际应用中存在一些限制和假设,例如市场是有效的、资产可以无限分割、投资者具有相同的预期、市场没有交易成本和税收等。
为了实现CAPM,我们需要以下步骤:
- 收集必要的数据:无风险收益率、特定证券的贝塔值和市场组合的预期收益率。
- 将这些数据代入CAPM公式计算证券的预期收益率。
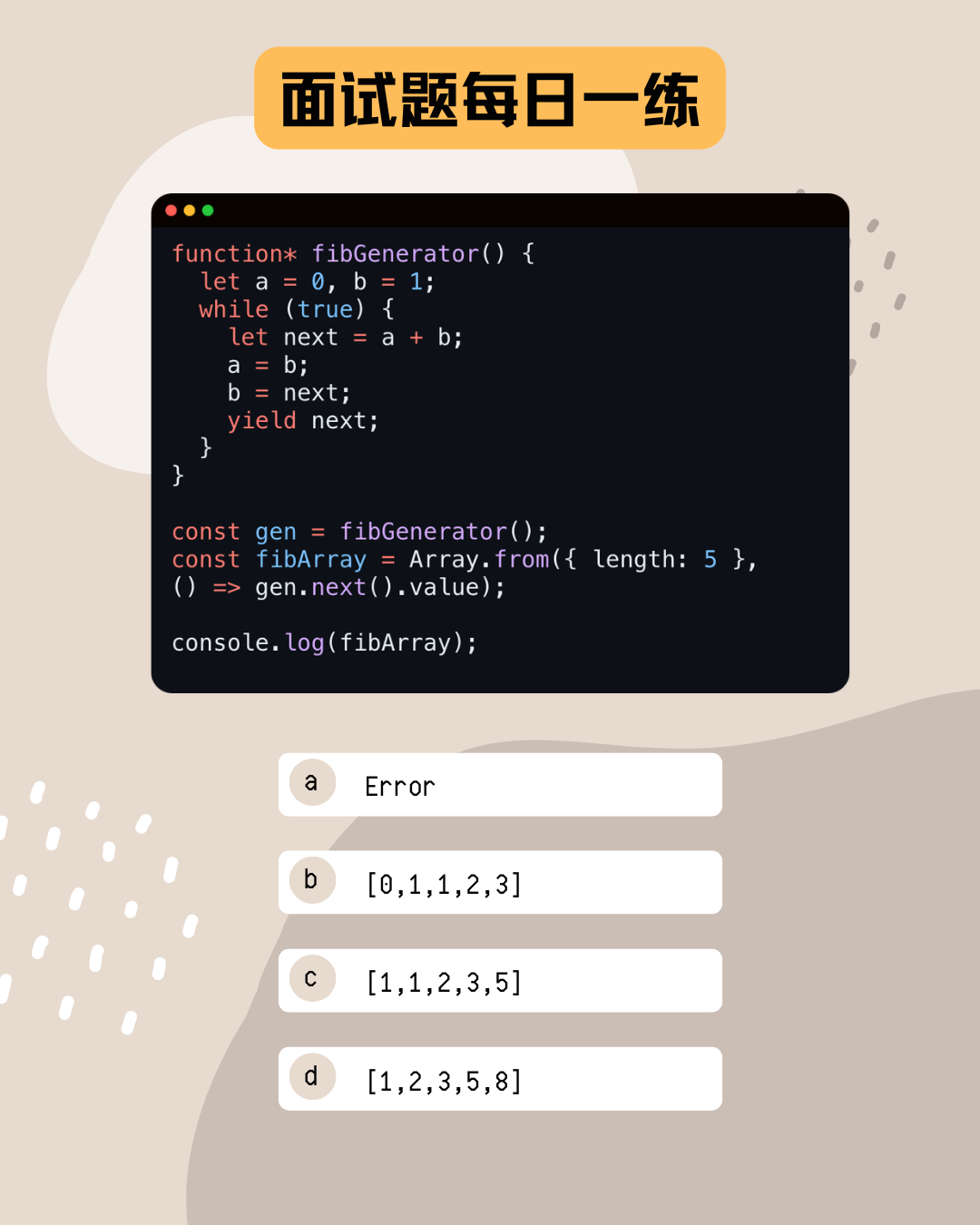
def capm_model(risk_free_rate, beta, market_return):
"""
计算证券的预期收益率,根据资本资产定价模型(CAPM)。
参数:
risk_free_rate (float): 无风险收益率
beta (float): 证券的贝塔值
market_return (float): 市场组合的预期收益率
返回:
float: 证券的预期收益率
"""
return risk_free_rate + beta * (market_return - risk_free_rate)
# 示例数据
risk_free_rate_example = 0.02 # 假设无风险收益率为2%
beta_example = 1.5 # 假设证券的贝塔值为1.5
market_return_example = 0.1 # 假设市场组合的预期收益率为10%
# 计算示例证券的预期收益率
expected_return_example = capm_model(risk_free_rate_example, beta_example, market_return_example)
expected_return_example
根据CAPM模型,使用示例数据计算得出,该证券的预期收益率为14%。
二:套利定价理论(APT)
套利定价理论(Arbitrage Pricing Theory,APT)是资本资产定价模型(CAPM)的一种扩展。APT理论基于多因子模型,认为证券的收益不仅仅受市场整体表现的影响,还受到多个宏观经济因素的共同影响,如通货膨胀率、利率、工业生产指数等 。
APT的核心在于无套利原则,即在一个有效的市场中,不应存在无风险套利的机会。如果市场未达到均衡状态,就会存在无风险套利机会。APT利用多个因素来解释风险资产收益,并根据无套利原则,得到风险资产均衡收益与多个因素之间存在近似的线性关系 。

APT与CAPM的主要区别在于:
- CAPM假设市场风险由单一的市场组合决定,而APT允许多个风险因子影响资产收益。
- APT不要求市场完全有效,而CAPM基于市场完全有效的假设。
- APT不需要投资者具有相同的投资理念,而CAPM假设投资者具有均值-方差偏好 。
APT理论在实际应用中,需要确定合适的风险因子,这通常基于历史数据和统计分析来实现。但它也面临着因子选择主观性等挑战。
def apt_model(alpha, betas, factor_returns):
"""
计算证券的预期收益率,根据套利定价理论(APT)。
参数:
alpha (float): 证券的特定常数项
betas (list of floats): 证券对各个因子的敏感性
factor_returns (list of floats): 各个因子的预期收益率
返回:
float: 证券的预期收益率
"""
return alpha + sum(beta * factor_return for beta, factor_return in zip(betas, factor_returns))
# 示例数据
alpha_example = 0.02 # 假设证券的特定常数项为2%
betas_example = [0.5, 0.3, -0.2] # 假设证券对三个因子的敏感性分别为0.5, 0.3, -0.2
factor_returns_example = [0.05, 0.02, -0.01] # 假设三个因子的预期收益率分别为5%, 2%, -1%
# 计算示例证券的预期收益率
expected_return_apt_example = apt_model(alpha_example, betas_example, factor_returns_example)
expected_return_apt_example
根据APT模型,使用示例数据计算得出,该证券的预期收益率为5.3%。
点下关注,分享更多有关AI,数据分析和金融工程相关的案例解析和实用教程。