探索数据结构：图(三)之最短路径算法

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 最短路径算法

最短路径问题可分为单源最短路径和多源最短路径。其指的是在带权有向图中，从某一顶点出发，找出通往另一顶点的路径，其中“最短”意味着该路径各边的权值总和达到最小。
其中单源最短路径是从图中的某一特定顶点出发，通往其他所有顶点的最短路径。与之不同，多源最短路径则是找出图中任意两个顶点之间的最短路径。

1.1 单源最短路径

解决单源最短路径的方法常见的有两种：Dijkstra(迪杰斯特拉算法)与Bellman-Ford(贝尔曼福特算法)。

1.1.1 Dijkstra

Dijkstra算法（迪杰斯特拉算法）是用于求解带权有向图中单源最短路径问题的算法。该算法以起始顶点为中心向外层层扩展，直到扩展到终点为止。它通过维护一个距离源点距离最短的顶点集合，每次从尚未确定最短路径的顶点中选择一个距离源点最近的顶点，将其加入到集合中，并更新与其相邻顶点到源点的距离。但是需要注意的是迪杰斯特拉算法要求权值为正数，如果有负数则可能出错。
二、算法步骤

初始化：

把图中所有顶点分为两部分，一部分是已确定最短路径的顶点集合（初始时只有源点），另一部分是未确定最短路径的顶点集合。
为每个顶点设置一个距离值，表示从源点到该顶点的当前最短路径长度（初始时，源点的距离值为 0，其他顶点的距离值为无穷大）。

重复以下步骤直到所有顶点都被加入到已确定最短路径的集合中：

从未确定最短路径的顶点集合中选择一个距离源点最近的顶点u。
将顶点u加入到已确定最短路径的集合中。
对于与顶点u相邻的每个顶点v，更新其距离值。如果通过顶点u到达顶点v的路径比当前已知的最短路径更短，则更新顶点v的距离值为从源点到顶点u的距离加上边<u,v>的权值。

算法结束后，每个顶点的最终距离值就是从源点到该顶点的最短路径长度。

首先选择s点作为起始点更新，更新两个离的最近t与y顶点。

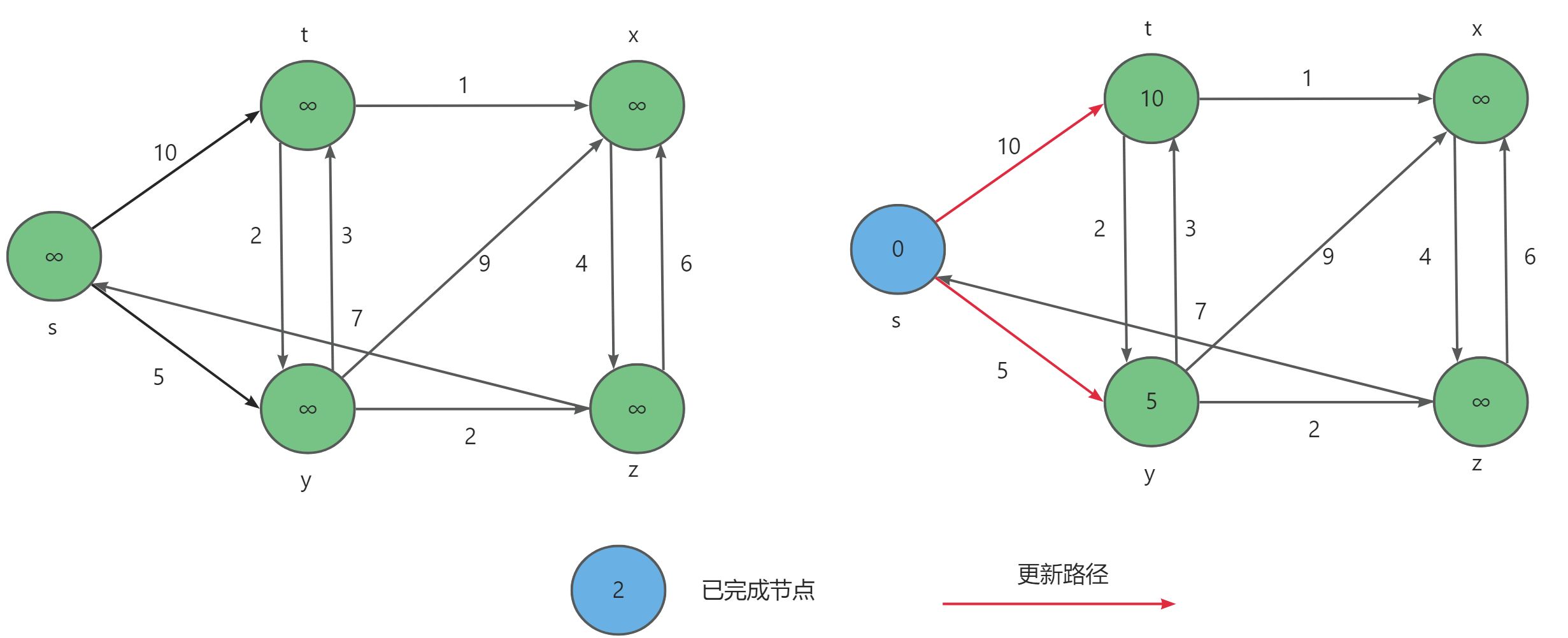
接下来选择已更新节点权值最小的顶点y出发继续更新顶点，首先t顶点会被再次更新，接着x与z顶点也会被更新。同理我们继续选择顶点z作为起始点，会再次更新x节点。

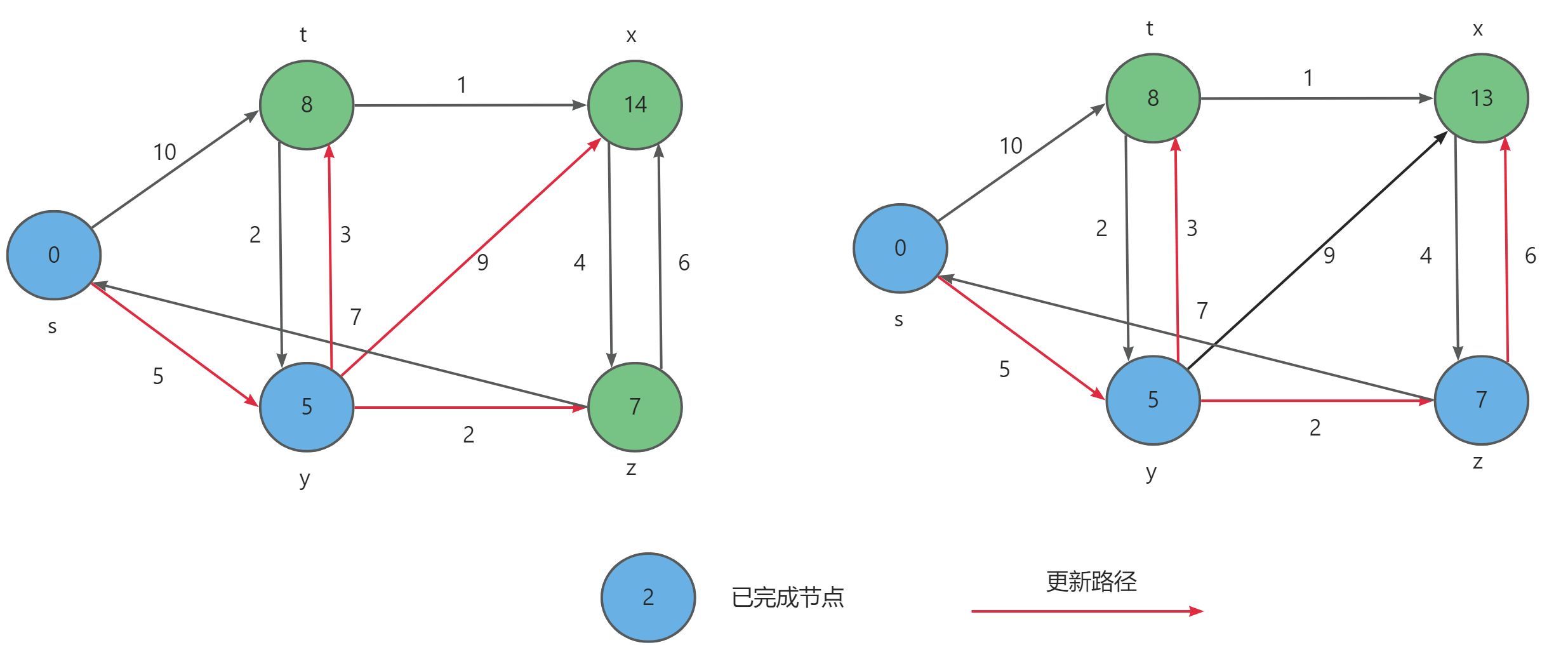
最后选择t顶点再次更新x顶点，最后选择x顶点更新完毕。

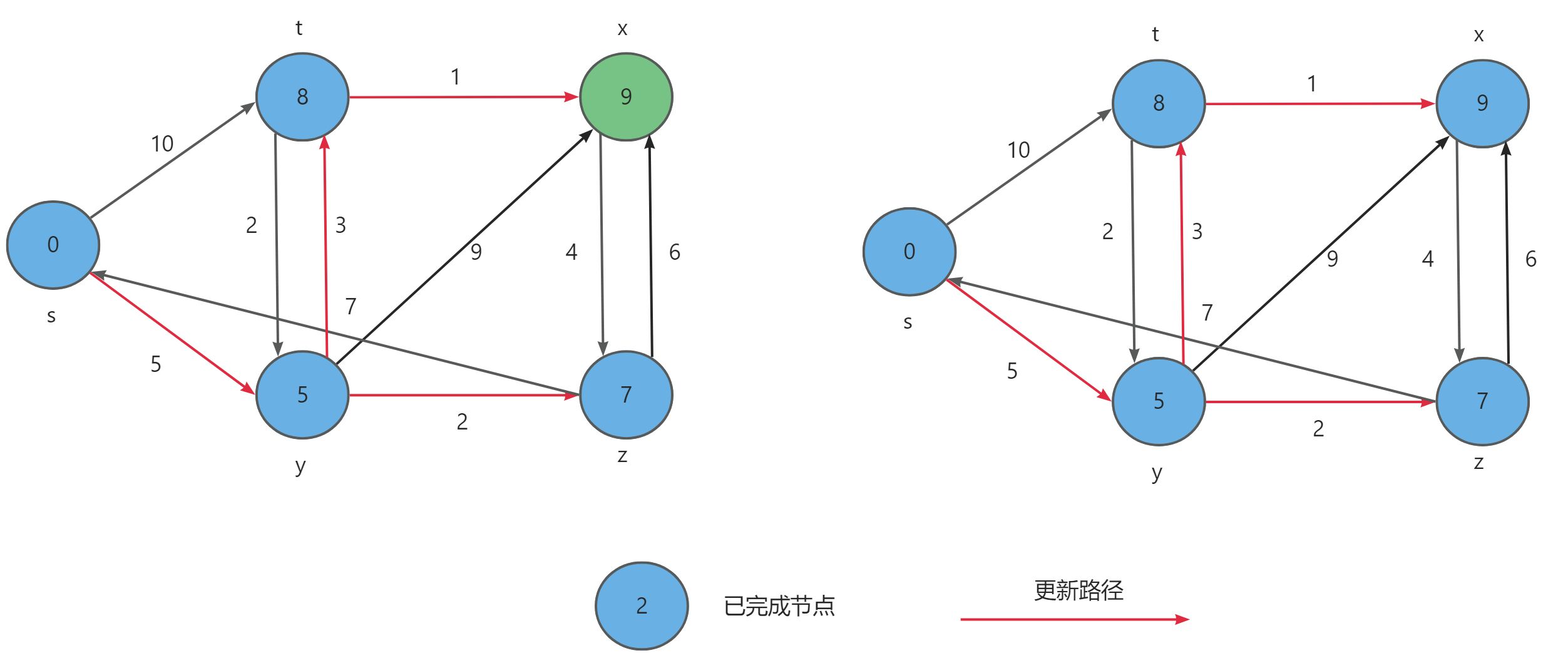
接下来我们需要实现Djikstra算法，首先我们可以创建一个pPath数组来记录到达各个顶点的前驱顶点，方便最后得出最短路径。然后进行初始化，并且创建一个bool数组来标记已确定加入集合的顶点，然后遍历所有顶点选择未加入集合且当前距离源点最小的顶点开始更新距离，更新之前先将该顶点标记。

//Dijkstra算法
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
    int n = _vertexs.size();
    int srci = getVertexsIndex(src);//获取源点下标
    dist.resize(n, MAX_W);//初始化
    pPath.resize(n, -1);//默认父节点下标为-1
    dist[srci] = W();//源点设为初始值
    vector<bool> visited(n, false);//已选中节点
    //更新n个顶点
    for (int i = 0; i < n; i++)
    {
        W minW = MAX_W;
        int u = -1;
        for (int j = 0; j < n; j++)
        {
            //选出距离的边记录其下标与权值
            if (visited[j] == false && dist[j] < minW)
            {
                minW = dist[j];
                u = j;
            }
        }
        //标记
        visited[u] = true;
        //进行松弛更新
        for (int v = 0; v < n; v++)
        {
            if (visited[v] == false && _matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v])
            {
                dist[v] = dist[u] + _matrix[u][v];
                pPath[v] = u;
            }
        }
    }
}

然后我们可以通过父节点更新出最短路径。

void PrinrtShotPath(const V& src, const vector<W>& dist, const vector<int>& pPath)
{
	int n = _vertexs.size();
	int srci = getVertexsIndex(src);
	for (int i = 0; i < n; i++)
	{
		vector<int> path;
		int cur = i;
		while (cur != -1)
		{
			path.push_back(cur);
			cur = pPath[cur];
		}
		reverse(path.begin(), path.end());
		for (int j = 0; j < path.size(); j++)
		{
			cout << _vertexs[path[j]] << "->";
		}
		cout << "权值为：" << dist[i] << endl;
	}
}

1.1.2 Bellman-Ford

Bellman-Ford算法也是用于求解带权有向图中单源最短路径问题的算法。与Dijkstra算法不同的是，Bellman-Ford算法可以处理图中存在负权边的情况。
算法步骤：

初始化：

为每个顶点设置一个距离值，表示从源点到该顶点的当前最短路径长度（初始时，源点的距离值为 0，其他顶点的距离值为无穷大）。

重复以下步骤V - 1次（V 是图中顶点的数量）：

对于图中的每一条边(u, v)，如果从源点到顶点u的距离加上边(u, v)的权值小于当前从源点到顶点v的距离，则更新顶点v的距离值为从源点到顶点u的距离加上边 (u, v) 的权值。

检测负权回路(回路权值为负)：

再对图中的每一条边进行一次遍历。如果在这次遍历中，还能找到一条边(u, v)，使得从源点到顶点u 的距离加上边(u, v)的权值小于当前从源点到顶点 v 的距离，那么说明图中存在负权回路。

算法结束后，如果没有负权回路，每个顶点的最终距离值就是从源点到该顶点的最短路径长度；如果存在负权回路，则无法得到正确的最短路径结果。

选取顶点s作为起始点，开始更新s-t与s-y的距离。

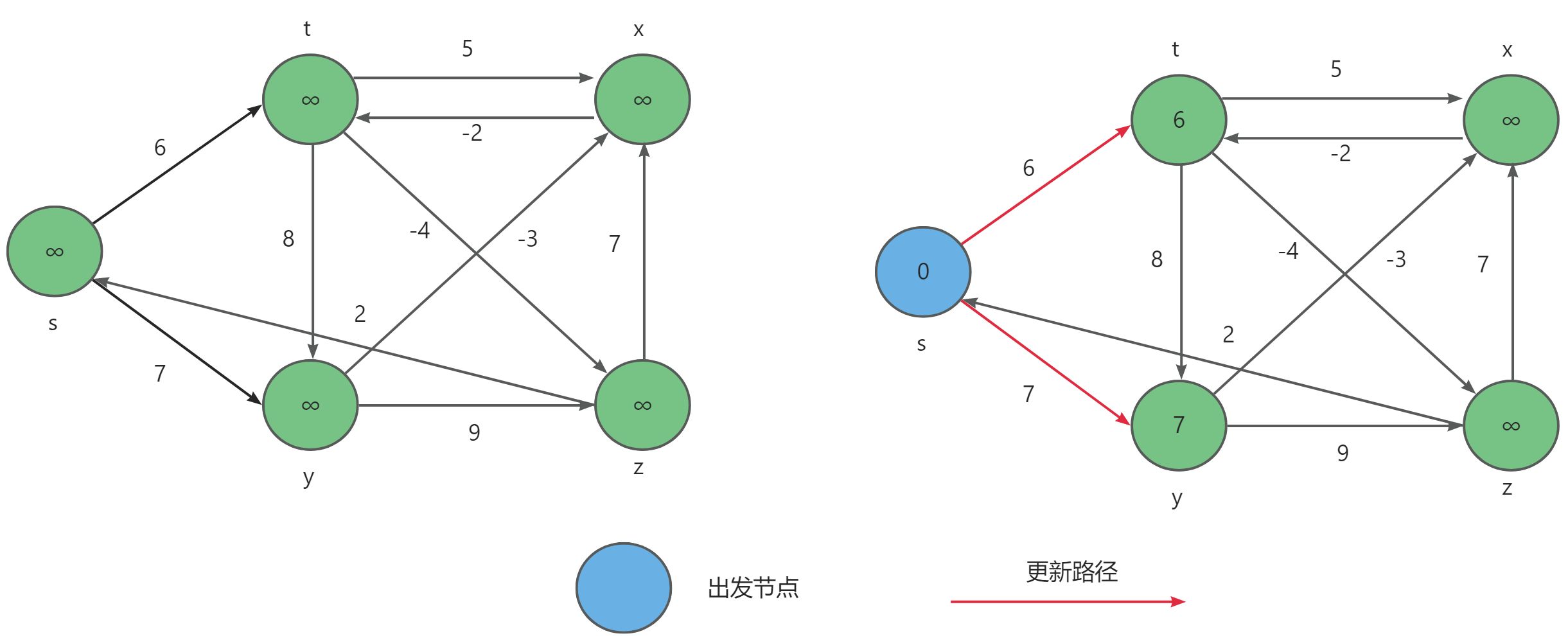
分别以顶点y与t作为起始点更新到达顶点x与z的距离。

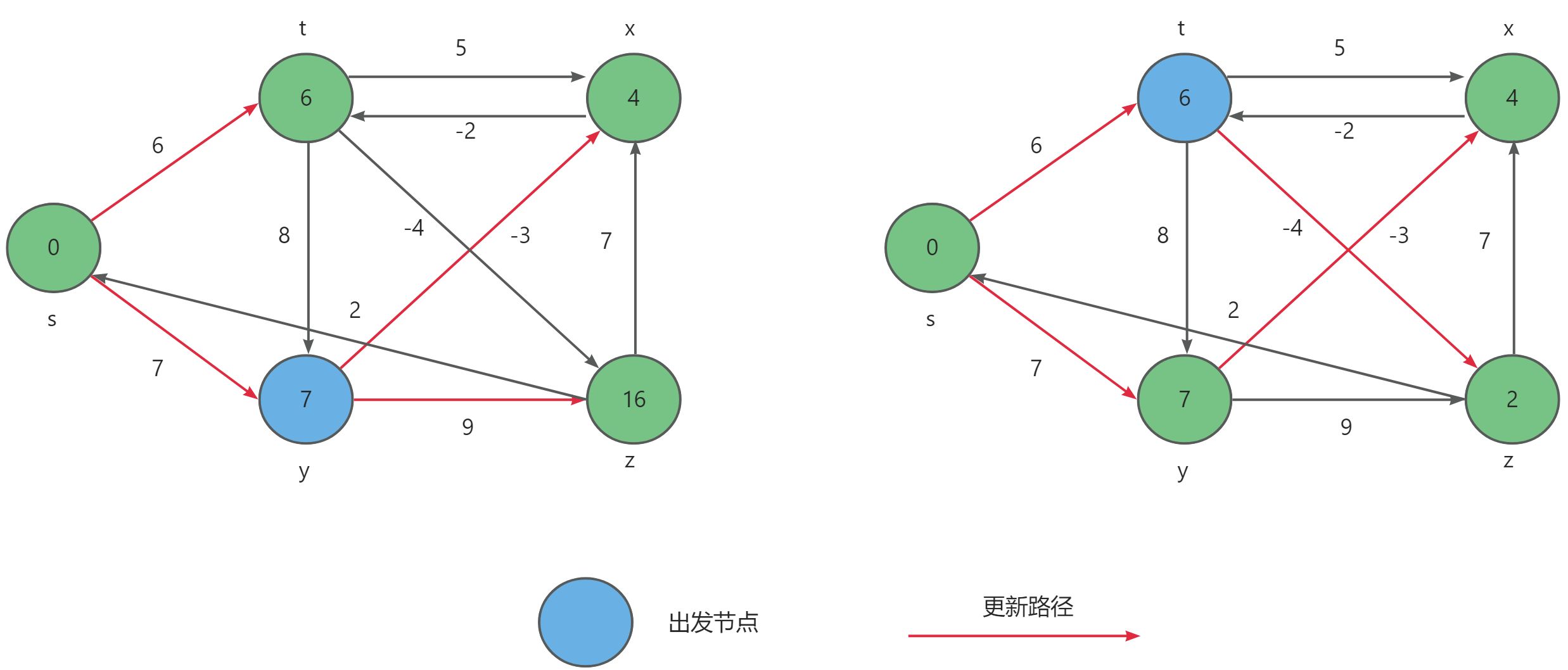
最后以顶点x与z点作为起始点更新距离，其中因为到达顶点t的最小距离s-t被再次更新，所以到达顶点z的最小距离s-t-z也需要被再次更新。

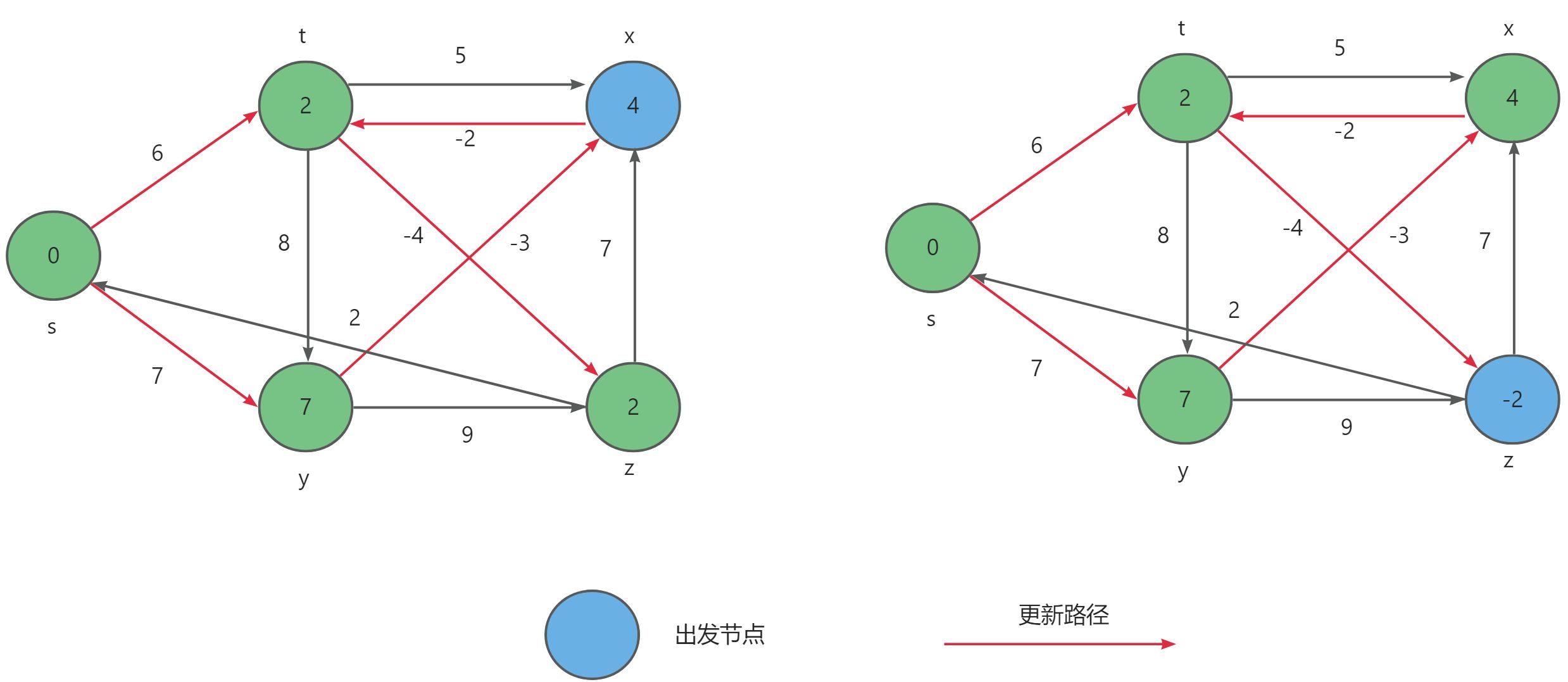
下来我们需要实现Bellman-Ford算法，同样我们可以创建一个pPath数组来记录到达各个顶点的前驱顶点，方便最后得出最短路径。然后只需要循环遍历每一个顶点，以该顶点为起始点更新其他顶点，最后重复V-1轮即可。

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexs.size();
	//获取源点下标
	int srci = getVertexsIndex(src);
	//初始化
	dist.resize(n, MAX_W);
	pPath.resize(n, -1);
	dist[srci] = W();
	//至多更新n-1轮
	for (int v = 0; v < n - 1; v++)
	{
		//判断是否发生更新
		bool update = false;
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				if (_matrix[i][j] != MAX_W && dist[i] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					dist[j] = dist[i] + _matrix[i][j];
					pPath[j] = i;
					update = true;
				}
			}
		}
		//如果未发生则直接退出
		if (update == false)
		{
			break;
		}
	}
	//判断是否存在负权回路
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
			{
				return false;//存在负权回路
			}
		}
	}
}

Bellman-Ford算法还有一个优化方案叫做SPFA（Shortest Path Faster Algorithm），主要是用一个队列来维护可能需要再次的顶点，避免了冗余的过程，但是这里不再重点介绍，感兴趣可以自行了解。
思考题：为什么要重复更新V-1次？

因为每一次更新可能使得前面已经更新过的路径的长度可以变得更短，或者使得某些源顶点之前不可达的顶点变得可达。比如说s->t->x先被更新，但是后续可能存在其他路径使得s->t路径更小，此时却并没有更新s->t->x路径。所以每一次更新只能使得至少能确定最短路径中的一条边，一个有V-1条边，所以至多更新V-1次。

1.2 多源最短路径

解决多源最短路径问题，虽然可以通过遍历每一个顶点使用Dijkstra或Bellman-Ford算法，但明显时间复杂度太高。而最常见的解决该问题便是Floyd-Warshall(弗洛伊德算法)，但是学习这种算法需要有点门槛，你得需要了解什么是动态规划。

1.2.1 Floyd-Warshall

Floyd-Warshall算法的原理基于动态规划。设 $D_{ij}$ 为从 $i$ 到 $j$ 只以 $1.. k$ 集合中的节点为中间节点的最短路径长度。

若最短路径经过点 $k$ ，则 $D_{i,j,k} = D_{i,k,k-1} + D_{k,j,k-1}$ ；
若最短路径不经过点 $k$ ，则 $D_{i,j,k} = D_{i,j,k-1}$ 。

因此， $D_{i,j,k} = \min(D_{i,j,k-1},D_{i,k,k-1} + D_{k,j,k-1})$ 。在实际算法中，为节约空间，可直接在原空间迭代，空间可降至二维。

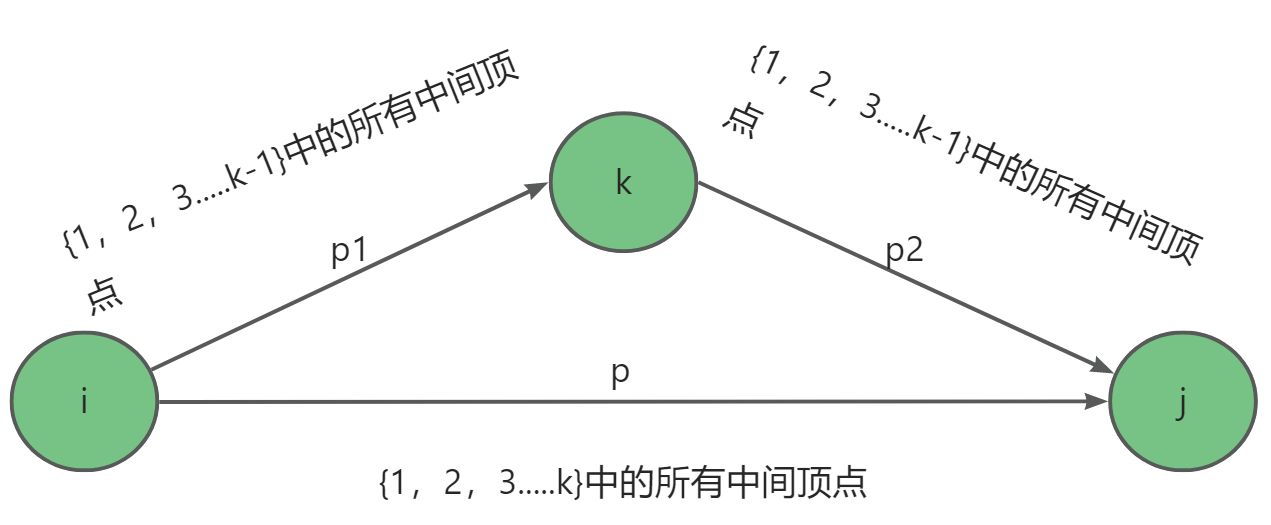
路径 $p$ 是从结点 $i$ 到结点 $j$ 的一条最短路径，结点 $k$ 是路径 $p$ 上编号最大的中间结点。路径 $p 1$ 是路径 $p$ 上从结点 $i$ 到结点 $k$ 之间的一段，其所有中间结点取自集合 $(1, 2, \dots, k - 1)$ 。从结点 $k$ 到结点 $j$ 的路径 $p 2$ 也遵守同样的规则。
算法步骤：

初始化：

构建两个二维数组，一个用于存储最短路径长度估计值 $D_{ij}$ ，初始时，若两点之间有直接边则为边的权值，否则为无穷大；另一个数组用于记录路径的前驱节点。

动态更新：

对于每个中间顶点 $k$ ，遍历所有的顶点对 $i$ 和 $j$ 。如果 $D_{ik} + D_{kj} < D_{ij}$ ，则更新 $D_{ij}$ 为 $D_{ik}$ + $D_{kj}$ ，并更新前驱节点。

下来我们需要实现Floyd-Warshall算法，同样我们可以创建一个pPath数组来记录到达各个顶点的前驱顶点，方便最后得出最短路径。然后只需要循环遍历每一个顶点，以该顶点为中间顶点更新其他顶点对。

//FloydWarshall
void FloydWarshall(vector<vector<W>>& dist, vector<vector<int>>& pPath) 
{
	//初始化
	int n = _vertexs.size();
	dist.resize(n, vector<W>(n, MAX_W)); 
	pPath.resize(n, vector<int>(n, -1)); 
	//初始化直接相连的边
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++) 
		{
			if (_matrix[i][j] != MAX_W) 
			{ 
				dist[i][j] = _matrix[i][j]; 
				pPath[i][j] = i; 
			}
			//顶点本身
			if (i == j) 
			{ 
				dist[i][j] = W(); 
			}
		}
	}
	//依次取每个顶点作为中间节点
	for (int k = 0; k < n; k++) 
	{ 
		//起始顶点
		for (int i = 0; i < n; i++) 
		{
			//结束顶点
			for (int j = 0; j < n; j++) 
			{
				// i->k + k->j 比 i->j前面更新的距离更短，则更新
				if (dist[i][k] != MAX_W && dist[k][j] != MAX_W &&
					dist[i][k] + dist[k][j] < dist[i][j]) 
				{ 
					dist[i][j] = dist[i][k] + dist[k][j]; 
					pPath[i][j] = pPath[k][j]; 
				}
			}
		}
	}
}

2. 复杂度分析

2.1 Dijkstra

时间复杂度：

时间复杂度为 $O(N^2)$ ，这里的 $N$ 代表图中顶点的数量。具体原因如下：

使用邻接矩阵存储图时，每次从未确定最短距离的顶点中找到距离最小的顶点需要 $O (N)$ 的时间，而总共要进行 $N$ 次这样的操作。对于每个确定了最短距离的顶点，更新其邻接顶点的距离也需要 $O (N)$ 的时间，因为需要遍历所有顶点。所以总的时间复杂度为 $O(N^2)$ 。

空间复杂度：

空间复杂度为 $O (N)$ 。主要原因是需要存储每个顶点到源点的距离以及该顶点是否已确定最短距离等信息。对于有 $N$ 个顶点的图，这些信息总共需要 $O (N)$ 的空间。具体来说：

需要一个标记数组来记录每个顶点是否已确定最短距离，这个数组的大小也为 $N$ 。
需要一个数组来存储每个顶点到源点的距离，这个数组的大小为 $N$ 。

2.2 Bellman-Ford

时间复杂度：

总体时间复杂度为 $O(N\times E)$ ，其中 $N$ 是图中顶点的数量， $E$ 是图中边的数量。

分析：Bellman-Ford算法需要对图中的边进行 $N - 1$ 轮遍历，每一轮遍历所有的边，以松弛操作来更新最短路径。对于每一轮，遍历所有边的时间复杂度为 $O (E)$ ，而总共进行 $N - 1$ 轮，所以时间复杂度为 $O(N\times E)$ 。
当使用邻接矩阵实现时，遍历图中的所有边的时间复杂度变为 $O(N^2)$ ，从而导致上述代码的时间复杂度变为 $O(N^3)$ 。

空间复杂度：

空间复杂度为 $O (N)$ 。

分析：主要需要存储每个顶点到源点的最短距离，以及一些辅助信息，这些信息总共需要 $O (N)$ 的空间。对于有 $N$ 个顶点的图，存储每个顶点的最短距离需要 $N$ 个空间，同时可能还需要一些额外的空间来存储中间状态等信息，但在整体空间复杂度中，占主导地位的仍然是存储顶点最短距离的空间，所以空间复杂度为 $O (N)$ 。

2.3 Floyd-Warshall

时间复杂度：

总体时间复杂度为 $O(N^3)$ ，其中 $N$ 是图中顶点的数量。

分析：Bellman-Ford算法需要对图中的边进行 $N - 1$ 轮遍历，每一轮遍历所有的边，以松弛操作来更新最短路径。对于每一轮，遍历所有边的时间复杂度为 $O (E)$ ，而总共进行 $N - 1$ 轮，所以时间复杂度为 $O(N\times E)$ 。
当使用邻接矩阵实现时，遍历图中的所有边的时间复杂度变为 $O(N^2)$ ，从而导致上述代码的时间复杂度变为 $O(N^3)$ 。

空间复杂度：

空间复杂度为 $O (N)$ 。

分析：主要需要存储每个顶点到源点的最短距离，以及一些辅助信息，这些信息总共需要 $O (N)$ 的空间。对于有 $N$ 个顶点的图，存储每个顶点的最短距离需要 $N$ 个空间，同时可能还需要一些额外的空间来存储中间状态等信息，但在整体空间复杂度中，占主导地位的仍然是存储顶点最短距离的空间，所以空间复杂度为 $O (N)$ 。