NOIP 2016 普及组 基础题5
21 从一个 4×4的棋盘(不可旋转)中选取不在同一行也不在同一列上的两个方格,共有( )种方法。
22 约定二叉树的根节点高度为 1。一棵结点数为 2016 的二叉树最少有( )个叶子结点;一棵结点数为 2016 的二叉树最小的高度值是( )
2 相关知识点
1) 树
线性结构(数组、链表等)中节点是首位相接一对一关系,在树结构中节点之间不再是简单的一对一关系,而是较为复杂的一对多的关系
树在现实中是可以找到例子的,比如现实中的族谱,亲戚之间的关系是层次关联的树形关系
数据结构中的 树 的名字由来,是因为如果把节点之间的关系直观展示出来,由于长得和现实世界中的树很像,由此得名
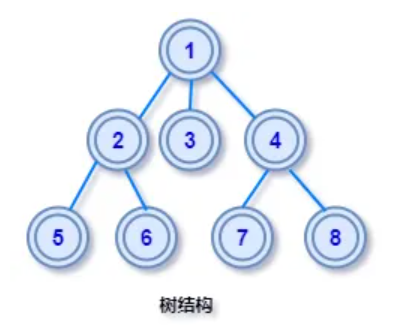
2) 树的相关概念
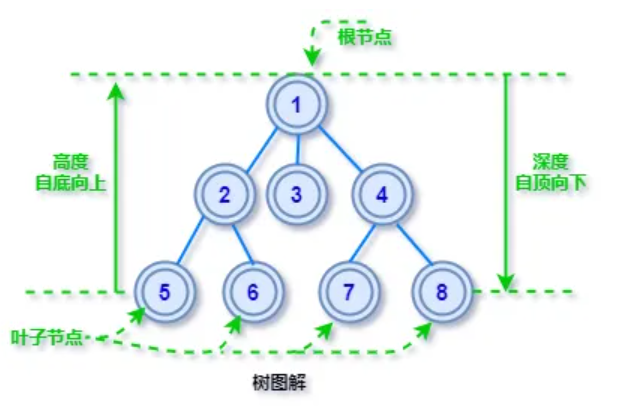
根节点
在一颗树形结构中,最顶层的那个节点就是根节点了,所有的子节点都源自它发散开来。
父节点
树的父子关系和现实中很相似,若一个节点含有子节点,则这个节点称为其子节点的父节点。
叶子节点
直观来看叶子节点都位于树的最底层,就是没有分叉的节点,严格的定义是度为 0 的节点叫叶子节点。
非叶节点
在树中的所有节点,除去叶子节点都为非叶节点
二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒
3) 组合
从n个不同元素中,任取m个元素,并成一组,叫做从n个 不同元素中取出m个元素的一个组合
从n个不同元素中选出来的m个元素,和顺序无关
例题
有10个人,规定相互通话一次,共通话多少次?
答案 45次
分析
2人通过,A与B通话1次,也是B与A通话1次,没有顺序区别
从10个里面任意选2人进行通话
C(10,2)=10*9/2=45
4) 组合数 排除法
当符合条件的情况繁杂而不符合条件的情况单一时,适合将不符合条件的情况从所有情况中减去
例题
从6名男生,5名女生中任选4人参加竞赛,要求男女至少各1名,有多少种不同的选法?
A.240 B.310 C.720 D.1080
分析
男女至少各一人的反面就是分别只选男生或者女生,这样就可以变化成C(11,4)-C(6,4)-C(5,4)=310
3 思路分析
21 从一个 4×4的棋盘(不可旋转)中选取不在同一行也不在同一列上的两个方格,共有( 72 )种方法。
分析
在一个4×4的棋盘中,每个方格可以用一个坐标(i,j) 来表示,其中i和j分别表示行和列的编号,范围是 1 到 4
首先,我们计算从 16 个方格中任选两个方格的总数
C(16,2)=16*15/2=120种
需要排除那些在同一行或同一列的方格对
同一行的方格对数
每行有 4 个方格,任选两个方格的组合数为
C(4,2)=4*3/2=6
4行,共有4*6=24种
同一列的方格对数
每列有 4 个方格,任选两个方格的组合数为
C(4,2)=4*3/2=6
4列,共有4*6=24种
所以方案数=120-24-24=72种
22 约定二叉树的根节点高度为 1。一棵结点数为 2016 的二叉树最少有( )个叶子结点;一棵结点数为 2016 的二叉树最小的高度值是( )
分析
二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒
可以每个节点只有一个子树,最后只有一个叶子节点
比如一棵结点数为 5 的二叉树,如下图,只有1个叶子节点E,找这个趋势下去,2016个节点也只有1个叶子节点
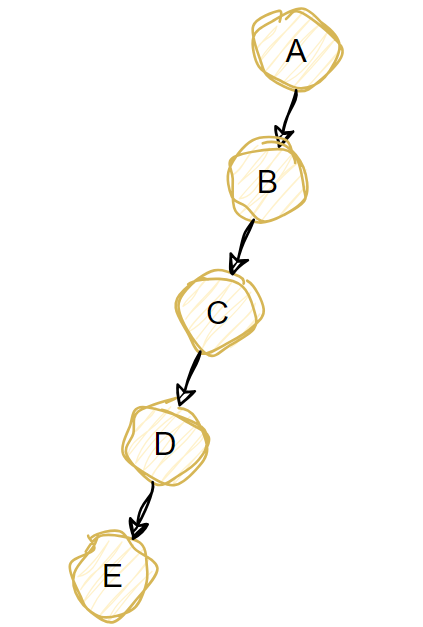
一棵结点数为 2016 的二叉树最小的高度值是( 11 )
要使高度最小,尽可能使得上层都是满的二叉树,除最后1层外其他层都是满的
以9个节点为例子,最小的高度为4,具体如下图
第1层 1个节点 2^0=1
第2层 2个节点 2^1=2
第3层 4个节点 2^2=4
前3层为1+2+4=7
第4层为2,总共9个节点,高位4
同样可以计算满节点的前n层的节点数
前1层 1个节点 2^0=1 -- 2^1-1=1
前2层 2个节点 2^1=2+1=3 -- 2^2-1=3
前3层 4个节点 2^2=4+3=7 -- 2^3-1=7
...
前10层 1023个节点 2^9=512+511=1023 -- 2^10-1=1023
前11层 1023个节点 2^10=1024+1023=2047 -- 2^11-1=2047
2016在1023和2047之间,所以需要高度为11