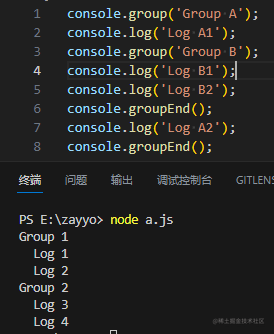
今天顺带加入了 bbr 的所有状态和所有流程,获得以下的方程组:
C = Bltbw,R = RtProp,T_r = ProbeRTT 周期,g1 = Startup gain,g2 = ProbeBW gain。设 x = estimated bandwidth,r = round trip time,w = inflight:
I ( t ) = ∑ i = 0 n w i ( t ) I(t)=\displaystyle\sum_{i=0}^n w_i(t) I(t)=i=0∑nwi(t)
d x d t = { ( g 1 − 1 ) x , r = R C ⋅ g 2 ⋅ x ⋅ r I ( t ) − x , r > R \dfrac{dx}{dt} = \begin{cases} (g_1-1)x, & r = R \\\\ C\cdot \dfrac{g_2\cdot x\cdot r}{I(t)}-x, & r \gt R \end{cases} dtdx=⎩ ⎨ ⎧(g1−1)x,C⋅I(t)g2⋅x⋅r−x,r=Rr>R
r ( t ) = { I ( t ) C , I ( t ) > C ⋅ R R , I ( t ) ≤ C ⋅ R r(t)=\begin{cases} \dfrac{I(t)}{C} ,& I(t)>C\cdot R\\\\R,&I(t)\leq C\cdot R \end{cases} r(t)=⎩ ⎨ ⎧CI(t),R,I(t)>C⋅RI(t)≤C⋅R
r m i n = min x ∈ [ t , t + T r ] r ( x ) r_{min}=\displaystyle\min\limits_{x\in[t,t+T_r]}r(x) rmin=x∈[t,t+Tr]minr(x)
d w x ( t ) d t = { x ( t ) ⋅ r m i n − w x ( t ) , t m o d T r ≠ 0 4 − w x ( t ) , t m o d T r = 0 \dfrac{dw_x(t)}{dt}=\begin{cases} x(t) \cdot r_{min}-w_x(t),& t\bmod T_r \neq 0 \\\\ 4-w_x(t),& t\bmod T_r = 0 \\ \end{cases} dtdwx(t)=⎩ ⎨ ⎧x(t)⋅rmin−wx(t),4−wx(t),tmodTr=0tmodTr=0
以下是该模型跑出来的一个多流(3 流,其中 z 流在 50 坐标位置加入)共存场景,python matplotlib 实现画图:

以下是用代码实现上述方程组后跑的一个单流场景,主要是为了和 bbr 论文相契合,C 实现,gnuplot 画图:

解释一个问题,为什么单流 bbr 没有进入 probertt,因为它不与任何流相互作用,故而能紧贴 C,时刻都能采集到 R。至于 g1 = 2.89 的推导,参见 The math behind dynamics of TCP BBR 。
这样的 bbr 描述看起来是不是非常干净,比看论文的文字描述清爽多了吧。当然,你可以根据自己的需求任意魔改,改代码变成了改方程,利用数学工具即所见即所得,是不是轻松了很多。经理们周末愉快。
浙江温州皮鞋湿,下雨进水不会胖。