RM惯性测量单元IMU

在Robomaster比赛中，一般各大参赛队会在机器人的云台上搭载IMU，用以反馈云台的yaw轴和pitch轴的角度和角速度。

需要注意的是，尽管依靠云台电机6020的编码器同样可以实现以上数据的获取，但是由于云台控制对于灵敏度和精度的要求比较高，而云台电机编码器反馈的数据分辨率较低，并且速度数据波动较大，用它来做控制并不能够达到很好的效果，所以目前的主流方案依然是通过IMU的数据来做云台的闭环控制。

IMU的选型方案非常多，从几十到几千乃至上万不等。一般IMU内部会包含陀螺仪和加速度计，陀螺仪用来反馈角速度和计算位姿，加速度计用于反馈线速度，陀螺仪和加速度各自提供三个轴向的速度数据，所以一般这种IMU被称为六轴IMU。基于不同原理去制作的陀螺仪和加速度计，能够达到的精度范围也有一定的区别。

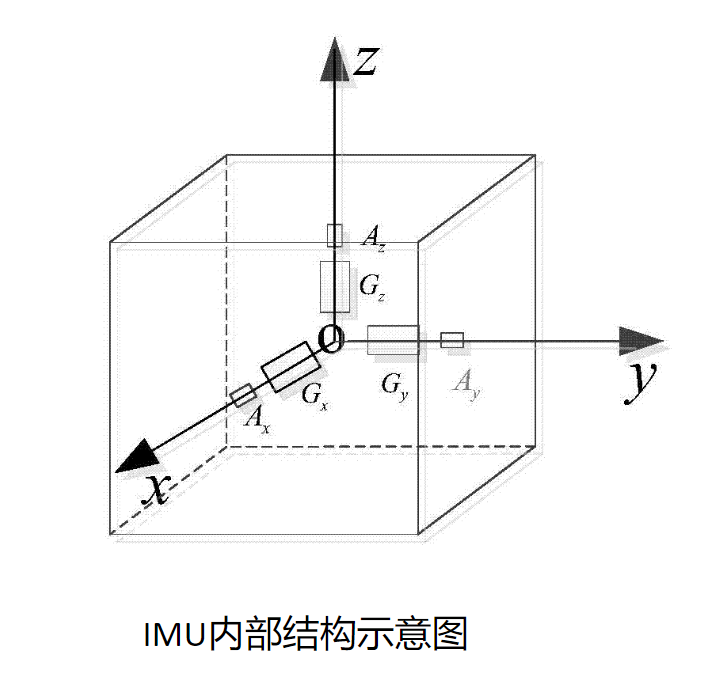
但是对于IMU来说，总会有一个难以克服的问题，即累积误差。由于IMU通过是通过对内部的陀螺仪获取的角速度数据对时间进行积分获取角度数据的，无论一个陀螺仪的精度有多高，总是会在每个时刻产生一些误差，随着积分效应，误差逐渐累积，最后就会产生累积误差。

为了解决累积误差问题，一般厂家会在IMU内部再集成一个三轴磁力计，从而构成一个所谓的九轴IMU。磁力计的作用是对IMU计算出的位姿定期进行较准，从而解决累积误差。但是磁力计不适合在电磁环境复杂的场合下使用，如果附近有能够产生强磁场的设备，会对磁力计的数据产生非常大的影响。

可以在下图中看到，比较常用的微机械陀螺仪（MEMS）其累积误差水平大概在每小时10°到100°。但是由于实际上每局比赛时间并没有那么长，所以其实累积误差造成的影响并不是特别严重，没有必要为了过高的精度要求而去购买特别贵的陀螺仪。

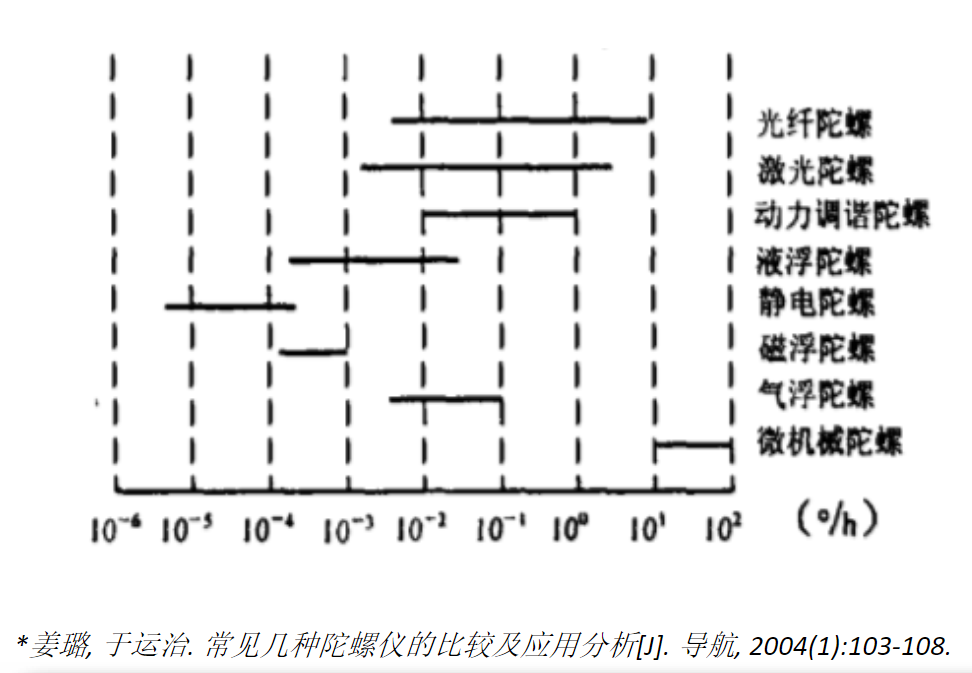
关于IMU的选型，不同的队伍有着不同的方案，而且一般来说都经过了若干次的迭代。

IMU选型上的坑很多，其中最严重的问题就是由于各种原因引发的复位/离线问题。在这种情况下，失去反馈的云台会立刻失控，从而发生“疯头”。

以下针对IMU总结一些需要注意的要点

确保供电稳定，如果供电电压有较大的波动可能会引发IMU掉线
确保物理防护，在赛场上的冲撞/弹丸打击可能会造成IMU的移位/掉线
确保陀螺仪量程，如果撞击产生了超出陀螺仪量程的大角速度，可能会引发云台偏移的问题
确保线路连接，保证通信线路电连接良好，尤其是当硬件方案涉及到比较长的走线时
IMU会受到温度影响，如果要在冬天时把机器人带到室外，记得采取一定的保温措施（比如加热电阻）

以下是一些防范IMU离线引发严重问题的方案

准备电机闭环方案，检测到IMU离线后可以自动/手动切换成电机编码器反馈
在云台上装载多个IMU，检测到一个离线后将反馈源切换成另一个
采用官方开发板/自研开发板上集成的IMU，相比独立的IMU模块来说风险更小

最后推荐一个讲IMU的知乎专栏，有兴趣的同学可以看一看。https://zhuanlan.zhihu.com/p/41299359

开发板板载IMU

官方提供的开发板自带IMU，用户手册中的介绍如下

如果要使用开发板板载IMU，则必须将开发板固定在云台上可以同时随着yaw轴与pitch轴运动的位置。板载IMU的需要自己完成姿态解算，姿态解算是通过SPI读取MPU6500的寄存器数据后，将三轴加速度计和三轴陀螺仪的数据进行数据融合，解算出当前的位姿，其中为了能够使用矩阵进行快速的运算，需要将欧拉角转换成四元数。

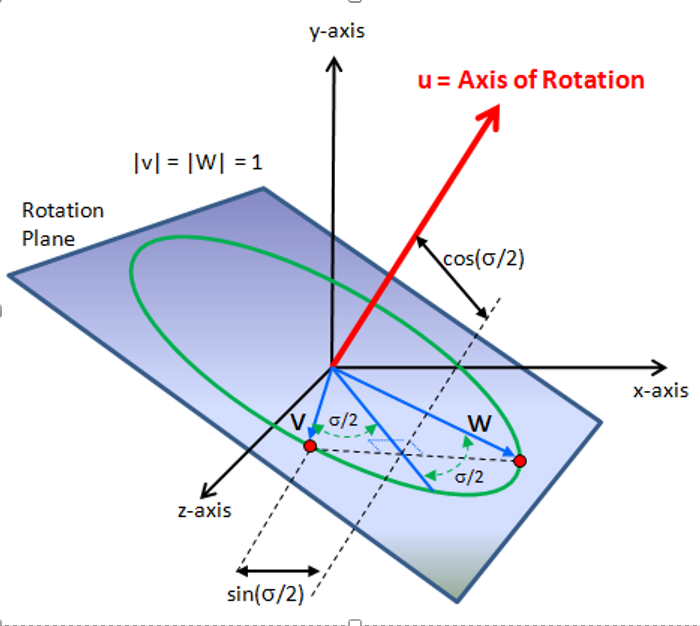
姿态解算的推导涉及到比较复杂的数学过程，这里就不加以太多的介绍了，有兴趣的可以自己去看下面的博客。

姿态解算

姿态解算-CSDN博客
mpu6050姿态解算与卡尔曼滤波（1）数学_mpu6050姿态解算与卡尔曼滤波(1)数学-CSDN博客

滤波

姿态估计（1）——互补滤波（Complementary filter ）-CSDN博客

四元数

彻底搞懂四元数-CSDN博客

牛顿迭代快速求根

牛顿迭代法快速寻找平方根 | Matrix67: The Aha Moments

官方车代码里面同样有解算的代码，并且有多种算法。下面这段代码是一个禁用了磁力计数据的算法，也是我自己以前移植到自己的工程里进行过测试的，由于当时我发现磁力计读取到的数据干扰很大，于是选择了禁用了磁力计数据的算法，只使用加速度计和陀螺仪进行数据融合。其中invSqrt是运用牛顿迭代法快速求平方根，是用于归一化处理的，官方给的注释在我看来已经已到位了，因此在这里不去加更多的注脚。

void mahony_ahrs_updateIMU(struct ahrs_sensor *sensor, struct attitude *atti)
{
  float recipNorm;
  float halfvx, halfvy, halfvz;
  float halfex, halfey, halfez;
  float qa, qb, qc;

  gx = sensor->wx;
  gy = sensor->wy;
  gz = sensor->wz;
  ax = sensor->ax;
  ay = sensor->ay;
  az = sensor->az;
  mx = sensor->mx;
  my = sensor->my;
  mz = sensor->mz;
  // Compute feedback only if accelerometer measurement valid (avoids NaN in accelerometer normalisation)
  if (!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f)))
  {

    // Normalise accelerometer measurement
    recipNorm = invSqrt(ax * ax + ay * ay + az * az);
    ax *= recipNorm;
    ay *= recipNorm;
    az *= recipNorm;

    // Estimated direction of gravity and vector perpendicular to magnetic flux
    halfvx = q1 * q3 - q0 * q2;
    halfvy = q0 * q1 + q2 * q3;
    halfvz = q0 * q0 - 0.5f + q3 * q3;

    // Error is sum of cross product between estimated and measured direction of gravity
    halfex = (ay * halfvz - az * halfvy);
    halfey = (az * halfvx - ax * halfvz);
    halfez = (ax * halfvy - ay * halfvx);

    // Compute and apply integral feedback if enabled
    if (twoKi > 0.0f)
    {
      integralFBx += twoKi * halfex * (1.0f / sampleFreq); // integral error scaled by Ki
      integralFBy += twoKi * halfey * (1.0f / sampleFreq);
      integralFBz += twoKi * halfez * (1.0f / sampleFreq);
      gx += integralFBx; // apply integral feedback
      gy += integralFBy;
      gz += integralFBz;
    }
    else
    {
      integralFBx = 0.0f; // prevent integral windup
      integralFBy = 0.0f;
      integralFBz = 0.0f;
    }

    // Apply proportional feedback
    gx += twoKp * halfex;
    gy += twoKp * halfey;
    gz += twoKp * halfez;
  }

  // Integrate rate of change of quaternion
  gx *= (0.5f * (1.0f / sampleFreq)); // pre-multiply common factors
  gy *= (0.5f * (1.0f / sampleFreq));
  gz *= (0.5f * (1.0f / sampleFreq));
  qa = q0;
  qb = q1;
  qc = q2;
  q0 += (-qb * gx - qc * gy - q3 * gz);
  q1 += (qa * gx + qc * gz - q3 * gy);
  q2 += (qa * gy - qb * gz + q3 * gx);
  q3 += (qa * gz + qb * gy - qc * gx);

  // Normalise quaternion
  recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
  q0 *= recipNorm;
  q1 *= recipNorm;
  q2 *= recipNorm;
  q3 *= recipNorm;
  atti->roll = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2 * q2 + 1) * 57.3; // roll     -pi----pi
  atti->pitch = asin(-2 * q1 * q3 + 2 * q0 * q2) * 57.3;                                // pitch    -pi/2----pi/2
  atti->yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2 * q2 - 2 * q3 * q3 + 1) * 57.3;  // yaw      -pi----pi
}

代码解释如下：

1、函数mahony_ahrs_updateIMU接收两个结构体作为参数接收两个结构体作为参数：sensor包含IMU传感器的数据，atti用于存储计算后的姿态角。

2、变量gx、gy、gz是陀螺仪测量的角速度，ax、ay、az是加速度计测量的加速度，mx、my、mz是磁力计测量的磁场强度。变量twoKp和twoKi是算法的控制参数，分别代表比例和积分增益的两倍。变量sampleFreq是传感器数据采样频率。