规则化建筑物

一、摘 要

        建筑物多边形在地图综合中的两类处理模型:化简与直角化。

        建筑物矢量数据来源广泛，在数据获取过程中，受GPS精确度、遥感影像分辨率或人为因素的影响，数据往往存在不同程度的误差。其中，图像分割、深度学习等技术提取的建筑物多边形边界由任意折线构成，直角特征弱，点数冗余，无法实现地理信息的规范化表达。本文讨论此类轮廓模糊建筑物的化简问题。

1.1 ArcGIS 规则化建筑物覆盖区 (3D Analyst)

        通过消除几何中不需要出现的伪影来对建筑物覆盖区面的形状进行规范化。

1.2 supermap 建筑物规则化

        通过提取建筑物的关键点及建筑物主方向，对建筑物覆盖区面的轮廓线进行规则化，用于消除建筑物范围几何中不规整的边界及细节。

1.3 学术学报 轮廓规则化

        （1）基于特征边重构的建筑物化简方法；

        （2）基于最小二乘的建筑物多边形的化简与直角化。

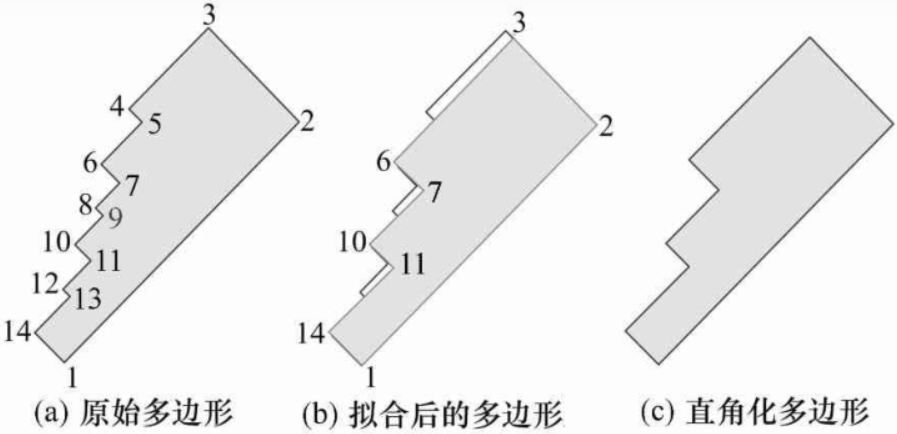
        建筑物的规则化处理，主要包括三个步骤：将特征边分组、重构，实现建筑物的有效化简，最后对化简后的多边形进行直角化处理。

二、特征边分组

        对待化简（规则化处理）的多边形，按某种规则，对多边形节点进行分组，通过分组节点获取特征边分组。

2.1 基于面主方向的特征边分组

        定义建筑物多边形中若干能控制多边形整体轮廓的边为特征边。以各边与主方向的夹角作为约束对建筑物轮廓进行了详细的划分。

01 主方向

        统计加权方法计算主方向考虑多边形每条边的方向和长度，避免了长边误差的干扰，其描述如下：

        ①测试0°至90°之间相差固定步长(步长取决于所需的结果精度，如1°)的一系列候选方向。

        ②对于每个候选方向，计算各边贡献值，候选方向的权重是每条边贡献值的总和。

        如下图，OA为候选方向，角度偏差系数为α。将多边形每条边平移，使其以点O为起点，若该边或其垂边在OB、OC范围内，则参与贡献值计算。多边形某边平移后为OD，由于在OB、OC范围外，贡献值为0；OE在范围内，长度为li，与OA夹角为β，则OE对候选方向OA的贡献值Li为：

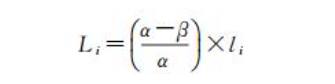
        统计加权法示意图如下：

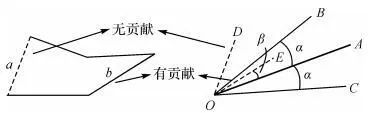
02 特征边分组

        设定边长系数l1、l2(l1＞l2)，特征边必须满足以下条件之一：

        ①边长大于l1；

        ②与主方向垂直或平行，且边长大于l2；

        ③存在与其垂直的邻边，且边长大于l2。保留多边形中的较长边有利于保持轮廓准确性，较长边的重构通常导致多边形变化过大，因此设置边长系数l1将此类边分类为特征边。通常l1为平均边长，l2用来约束化简程度。

        建筑物多边形中一条或连续几条非特征边为待化简弧段。以下图为例，特征边分组的过程如下：

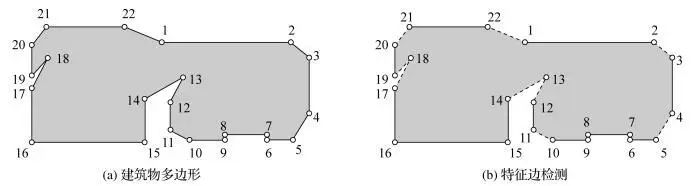
        (1) 遍历建筑物多边形点集合，判断相邻两点间线段与主方向的空间关系并计算两点间距，若该线段不是特征边，记录首点点号，得到非特征边点集合S1{2, 4, 6, 8, 10, 12, 13, 17, 18, 20, 22}。

        (2) 根据集合S1计算待化简弧段的点集合，得到集合S2{[2, 3], [4, 5], [6, 7], [8, 9], [10, 11], [12, 13, 14], [17, 18, 19], [20, 21], [22, 1]}。

        (3) 待化简弧段两侧特征边的组合集S3为{[1, 2;3, 4], [3, 4;5, 6], [5, 6;7, 8], [7, 8;9, 10], [9, 10;11, 12], [11, 12;14, 15], [16, 17;19, 20], [19, 20;21, 22], [21, 22;1, 2]}。

2.2 基于距离阈值和直角约束的特征点分组

        建筑物多边形主要是由相互垂直的弧段构成，一般可分解成多个大小不一的矩形。

        对其化简的目的是在保持多边形整体轮廓一致的前提下,删除若干个小的凸起矩形，补平若干个凹陷矩形。

        在多边形的点集中，总存在若干能控制多边形整体轮廓的点，这些点相对其它点而言，化简后位移距离较小，本文称这些点为建筑物多边形的特征点。

        对常规的地图，可根据比例尺计算出最小可视距离，但在多尺度地图综合中最小可视的实地距离不仅与目标比例尺有关，而且与源地图的比例尺有关。这里按“自然规律”的综合法则来计算。

01 最小可视距离阈值的计算

        F= St*D[ 1 - Ss/ St ] ,

        式中：

        F为目标比例尺下图上最小可视距离对应的实地距离；

        St为目标比例尺分母；

        D为最小可视的距离,取值为0.3～0. 6 mm；

        Ss为源数据比例尺分母.

        在源比例尺为1 :2 000、目标比例尺为1∶1万,取最小可视距离D=0. 4 mm ,计算得F=3. 2m。

02 特征点分组

        建筑物分组的具体步骤:

        （1）将多边形的坐标点按逆时针方向排序；N为多变形点的总数。设置4个变量A、B、E、F表示当前要判断边的点号，其中A、B用于顺时针方向搜索，E、F用于反时针方向搜索。设置变量s表示第1组的起点。

        （2）找到最长的一条边，该边两个端点的序号为n， n+1 ，初始化一个整数链表LIST，将n， n+ 1插入该链表。令A= E= n,B = F= n+1；

        （3）沿A向顺时针方向搜索两个点，其点号：A=(A - 2)%N，B = (B - 2)% N ；

        （4）在LIST对应的点构成的弧段中，存在若干与A - B平行(包括近似)的弧段，计算AB到这些弧段的最大距离d ；以及A→B到n →n+1的夹角a；

        （5）如果d >F或者d <F且a >0°，表示已找到第1组的起点，则令S = (A +2)%N，继续搜索F的下两点，其点号E= (E+ 2) % N，F= (F+ 2) % N，到步骤6；否则在LIST首位置加入B、A，继续向上搜索，回到步骤3；

        （6）如果F=S，则分组完毕，结束探测。否则，与步骤3一样，计算EF到与之平行的弧段的最大距离d以及E→F到n →n＋1的夹角α；

        （7）如果d >F或者d <F且a >0°，则该组搜索完毕，开始探测下一组，重新初始化一个新链表LIST，向前进方向搜索新组。如果不满足上述条件，则将E、F加入到LIST，令 E=（E＋2)% N，F=（F＋2)% N，回到步骤5。

        对建筑物多边形的点进行分组，如下图所示：

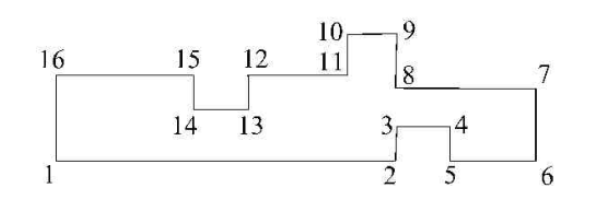
        多边形的点分成了4个组：( 1、2、3 、4 、5 、6)， (6、7)，(7 、8、 9、 10、11、 12、13 、14、15、16) ， (16、1 ) 。

三、特征边重组原则

        基于特征边组合的判别和重组来化简建筑物多边形，基本目标是实现建筑物多边形与影像建筑物边界最大程度的套合，并尽可能保持面积和形态特征。因此，结构重组时按照以下原则：

        原则1：用边长系数l2和局部区域面积l3(l3=l22)约束化简程度。

        原则2：结构重组是一个循环的过程，每处理完一个局部结构，更新多边形，再次进行特征边分组、重构，直到特征边组合集为空集。

        原则3：对于凹凸结构不进行夸大处理，若满足删除(填充)条件，删除(填充)后循环过程将再次判别并处理此弧段。

四、结构重组

        对分组后的每组特征边，都需要提取一条线段来代替这一组折线边集合，可以采取特征点拟合直线、或凸多边形最窄宽度提取中心线等实现。将分组提取替代线按一定的规则，进行连接处理，便可实现结构的重组。

        由于特征边与主方向的关系多为平行或垂直，待化简弧段两侧特征边的空间关系组合可抽象为3种，分别为平行结构、垂直结构和其他结构。

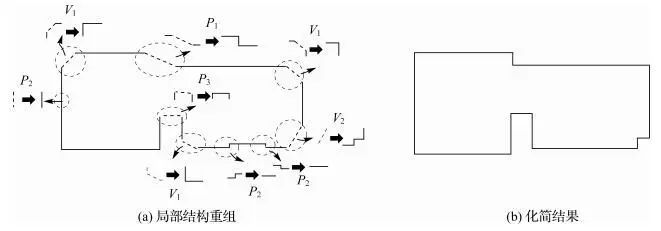
        判断邻近替代线的空间关系，以夹角、位置作为选择化简规则的条件，通过局部结构重组实现化简。化简示意图如下：

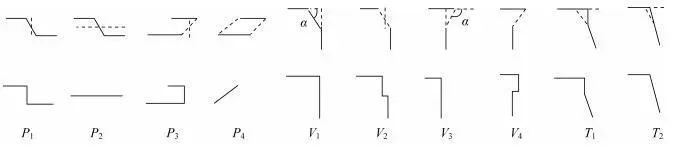
4.1 平行结构

        P1、P2、P3、P4为平行结构，待化简弧段两侧特征边平行。

        （1）若两边间距大于l2，过待化简弧段中点向两侧作垂线，如P1、P3。

        （2）否则，判断两边夹角，若夹角为0°，采用最小二乘法将该结构(包括待化简弧段)的点拟合成直线替代该结构，如P2（理论上不存在）；

        （3）若夹角为180°，该结构面积小于l3，连接端点，删除凸起(填充凹陷)的部位，如P4，若该结构面积大于l3，按P3处理。

4.2 垂直结构

        V1、V2、V3、V4为垂直结构，待化简弧段两侧特征边垂直。

        （1）V1、V3结构中，α小于90°，计算两边交点，若该点与邻近两点组成区域面积小于l3，则添加交点，如V1；

        （2）否则, 取虚线中点，向两侧作垂线，如V2。若α大于90°，如V3、V4，若两边交点与邻近两点组成的区域面积小于l3，添加交点，删除右侧区域，如V3，否则，取虚线中点，如V4。

4.3 其他结构

        T1、T2为其他结构，两特征边既不垂直也不平行。计算斜边一点到另一边的距离，若距离大于l2，添加垂线与另一边的交点，如T1，否则直接添加交点，如T2。

五、直角化规则

        若建筑物目标中两相邻边满足规则化空间关系，判断两边与主方向的关系，以主方向为基准进行直角化处理。直角化规则如下：

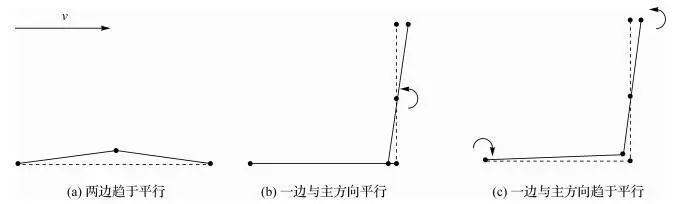
        (1) 若两边共线或趋于平行，则移除中间点，如图 (a)所示。

        (2) 若两边趋于垂直，其中一边与主方向平行或垂直，将另一边绕其中点旋转至二者垂直，如图 (b)所示。

        (3) 若两边趋于垂直，其中一边与主方向趋于平行或趋于垂直，将其绕端点旋转至主方向或主方向的垂直方向，另一边绕中点旋转至二者垂直，顶点移至二者交点，如图 (c)所示。

        (4) 若两边趋于垂直，且两边均不与主方向接近平行或垂直，将较短边绕中点旋转至二者垂直。

六、建筑物规则化（实现） --- 特征边分组、重构、直角化 

ME & OTHERS

虚心学习、借鉴、优化

        在虚心学习了大家的成果后，畅想着“建筑物规则化”在制图和数据规则化上有很好的应用需求，规则化后的建筑物轮廓，在使用“建筑物2.5D效果”工具时，不但因为节点的减少提高工具分析性能，还因为直角化让建筑物更加规范、立体。

        最重要的是，基于特征分组和规则化允许偏移距离的融合，让我豁然开朗，不仅可以用来处理具有正交特性的建筑物，还可以拓展用于简化非正交的，曲线特征的图形。如通过影像实例分割得到的水系、道路等数据。

        具体算法和实现在后续的文章中讲解。本文给出实现的过程视频。

        本文基于下图，演示特征边分组、重构和直角化的实现过程。

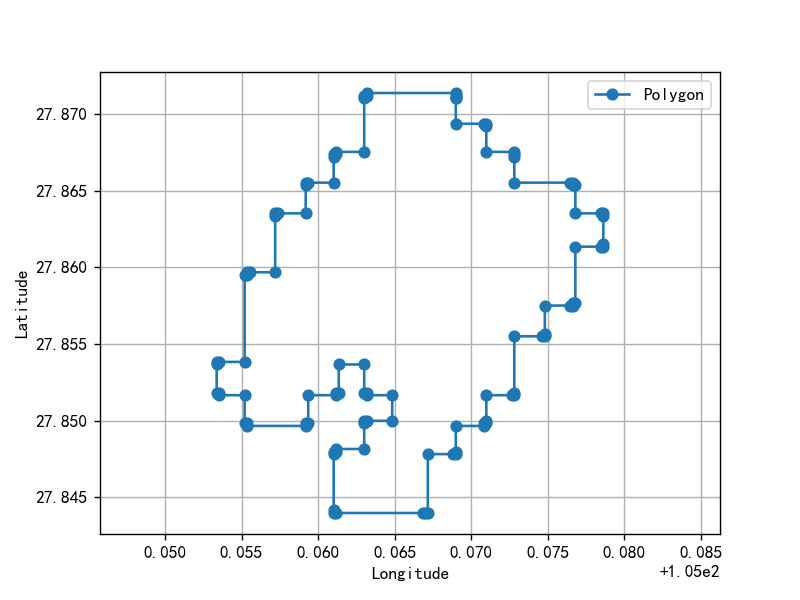
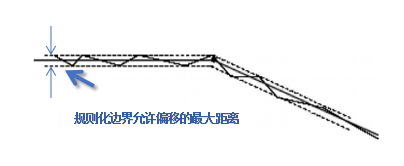
6.1 基于偏移距离的特征边分组

        假设我们有一支很粗的笔，沿着多边形边界绘制，当前画笔定能掩盖需要被简化的短边、不规则折线。

        当绘制建筑物轮廓时，应确保绘制线段保持直线连接。绘制曲线段时，确保曲线的平滑过渡。

6.2 特征分组重构

        特征边重构，由于考虑的是“笔画”遮盖的效果，故提取笔画的中心线作为重构线结果，比使用“基于最小二乘平差模型的线性拟合”更加符合小编的算法设计。

        因此，可将重构算法转为凸多边形最小宽度算法+凸多边形在指定方向上的中心线提取。

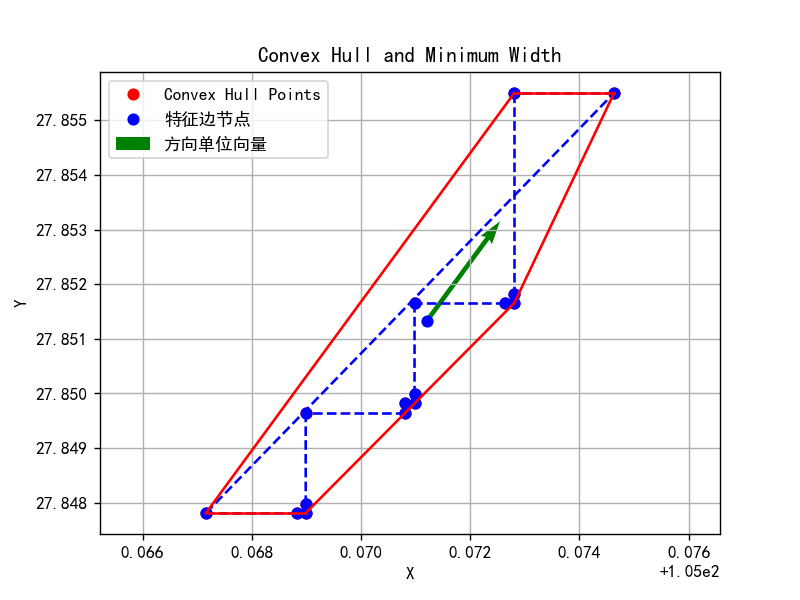
        凸多边形的宽度定义为平行切线间的最小距离，可使用“旋转卡壳”算法实现。

        凸多边形在垂直于最小宽度方向上的中心线提取，可使用分组起始点和结束点在方向单位向量上的投影点获取。

        分组特征边计算重构线算法示意如下图：

        重构线结果示意如下图：

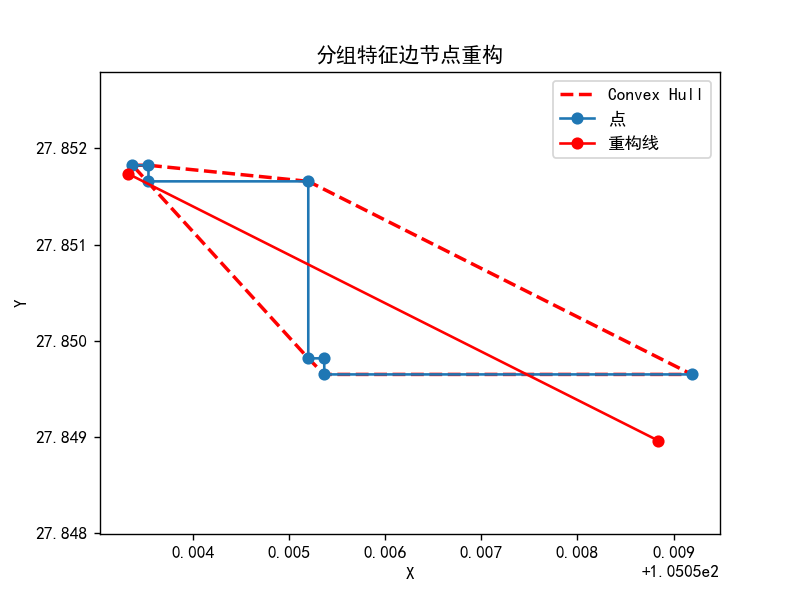
特征边分组、重构过程（迭代）演示如下

6.3 多边形直角化

        由于并非所有建筑物的内角均应为直角，且其长边与短边在直角化处理中影响力(权)不同，因此，可使用带限制条件的建筑物多边形不等权的局部直角化的最小二乘算法实现建筑物的直角化。

        建筑物多边形直角化过程示意如下图：

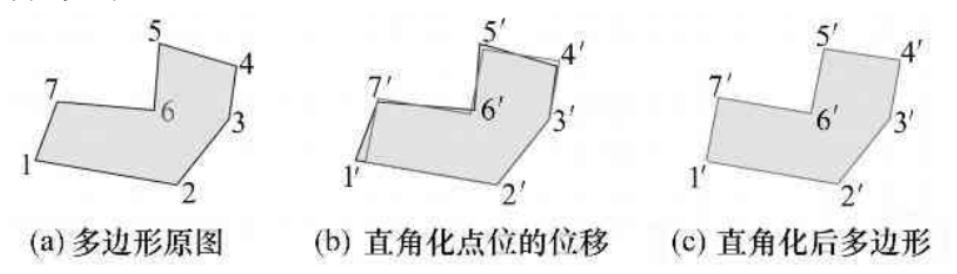
直角化过程（迭代）演示如下：