62、不同路径
题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
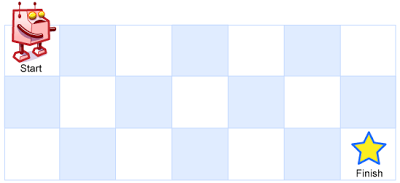
输入:m = 3, n = 7 输出:28
代码
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n]; //dp[i][j]表示走到该网格有几种路径
//dp数组初始化,最上面和最左面要初始为1
for(int i=0; i < m; i++){
dp[i][0] = 1;
}
for(int j=0; j < n; j++){
dp[0][j] = 1;
}
//遍历顺序:从左向右+从上到下
for(int i=1; i < m ; i++){
for(int j=1; j < n; j++){
//该网格的路径=上面+左边之和
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1]; //返回最右下角的网格
}
}63、不同路径II
题目
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
代码
class Solution {
//有障碍的初始化区别:网格有障碍,右边和下面的就不初始化1,默认0了
//有障碍的递推区别:有障碍的不能用递推公式,默认=0
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length; //行数
int n = obstacleGrid[0].length; //列数
int[][] dp = new int[m][n]; //dp[i][j]表示走到这个网格的路径个数
//dp数组初始化:无障碍左边和上面全为1,有障碍,不处理后面默认全为0
for(int i=0; i < m && obstacleGrid[i][0] == 0; i++){
dp[i][0] = 1;
}
for(int j=0; j < n && obstacleGrid[0][j] == 0; j++){
dp[0][j] = 1;
}
//遍历顺序:从上往下+从左往右
for(int i=1; i < m; i++){
for(int j=1; j < n; j++){
//无障碍=左边+上面之和
if(obstacleGrid[i][j] == 0){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
//有障碍,该网格不能走,路径直接归零
else{
dp[i][j] = 0;
}
}
}
return dp[m-1][n-1]; //返回左下角
}
}343、整数拆分
题目
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
代码
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n+1]; //dp[i]表示把i拆分的乘积最大值
//dp数组初始化
dp[1] = 0; //0*1
dp[2] = 1; //1*1
//遍历顺序,从3-n进行拆分,计算dp[i]
for(int i=3; i <= n; i++){
//对i进行拆分
//用3举例:3=1+2/dp[2],3=2+1/dp[1]
//用4举例:4=1+3/dp[3],4=2+2/dp[2],4=3+1/dp[1]
for(int j=1; j < i; j++){
int two = j * (i - j); //把i拆成两数相乘
int three = j * dp[i-j]; //把i拆成多数相乘
//求max的时候dp[i]不能漏,因为two和three只是把i进行j的两种拆分,但不一定的dp[i]拆分的最大值
dp[i] = Math.max(dp[i], Math.max(two, three)); //递推公式
}
}
return dp[n];
}
}96、不同的二叉搜索树
题目
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
代码
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1]; //dp[i]表示i个节点的二叉搜索树的个数
//dp数组初始化
dp[0] = 1; //空树是一个二叉搜索树
//遍历顺序:i从1-n分别计算二叉搜索树的个数dp[i]
for(int i=1; i <= n; i++){
//对i个节点进行拆分,以1为头结点-以i为头结点的情况分别求和,得到dp[i]
for(int j=0; j < i; j++){
//以i=3举例
//dp[3] = 以1头结点+以2头结点+以3头结点
//dp[3] = dp[0]*dp[2] + dp[1]*dp[1] + dp[2]*dp[0](左子树*右子树)
int tmp = dp[j] * dp[i-1-j]; //递推公式
dp[i] += tmp;
}
}
return dp[n]; //返回n个节点的个数
}
}


















