文章目录
- 01背包
- 代码
- 完全背包
- 代码
- 多重背包
- 代码
- 混合背包
- 代码
- 二维费用的背包问题
- 代码
- 分组背包问题
- 代码
- 有依赖的背包问题
- 代码
- 背包问题求方案数
- 代码
- 背包问题求具体方案
- 代码
01背包
有
N
N
N 件物品和一个容量是
V
V
V 的背包。每件物品只能使用一次。
第
i
i
i 件物品的体积是
v
i
v_i
vi,价值是
w
i
w_i
wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有
N
N
N 行,每行两个整数
v
i
,
w
i
v_i, w_i
vi,wi,用空格隔开,分别表示第
i
i
i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0
<
N
,
V
≤
1000
0 \lt N, V \le 1000
0<N,V≤1000
0
<
v
i
,
w
i
≤
1000
0\lt v_i, w_i \le 1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
代码
// 暴力 朴素 法
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N][N]; // 二维的f[i][j],前 i 个物品,体积不超过 j 的最大值
int v[N],w[N]; // 储存 体积 和 价值
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 利用上次的更新的 f 数组
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j]; // 不选第 i 个物品,体积不超过 j 的最优解
// 满足选择第 i 个物品,体积不超过 j-v[i] 的最优解
if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
}
cout<<f[n][m];
return 0;
}
// 优化一次,由上述的暴力 朴素 法,可知转化成为一维数组对最后的结果无影响
#include<bits/stdc++.h>
using namespace std;
int f[1010];
int v[1010],w[1010];
int main()
{
int n,s;cin>>n>>s;
for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 利用上次的更新的 f 数组
for(int j=s;j>=0;j--)
{ // 满足选择第 i 个物品,体积不超过 j-v[i] 的最优解
if(j>=v[i]) f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[s];
return 0;
}
// 终极版本 时间复杂度:Θ(V∗N) 空间复杂度:Θ(V)
#include<bits/stdc++.h>
using namespace std;
int f[1010],v[1010],w[1010]; // 状态转移方程变为 一维 ,优化利用上次的 f[i]
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 从大到小枚举,利用上一层次的f[i](完全背包为从小到大,利用本层次的f[i])
// 由上述优化一次得,枚举到 v[i] 即可
for(int j=m;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m];
return 0;
}
完全背包
有
N
N
N 种物品和一个容量是
V
V
V 的背包,每种物品都有无限件可用。
第
i
i
i 种物品的体积是
v
i
v_i
vi,价值是
w
i
w_i
wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有
N
N
N 行,每行两个整数
v
i
,
w
i
v_i, w_i
vi,wi,用空格隔开,分别表示第
i
i
i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0
<
N
,
V
≤
1000
0 \lt N, V \le 1000
0<N,V≤1000
0
<
v
i
,
w
i
≤
1000
0 \lt v_i, w_i \le 1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
代码
// 朴素法
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N][N]; // 二维的f[i][j],前 i 个物品,体积不超过 j 的最大值
int v[N],w[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 利用到 本次和上次 的更新的 f 数组
for(int j=0;j<=m;j++)
{
f[i][j]=f[i-1][j]; // 不选第 i 个物品,体积不超过 j 的最优解
if(j>=v[i]) // 选第 i 个物品,体积不超过 j 的最优解
f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}
}
cout<<f[n][m];
return 0;
}
// 一次优化,由朴素法得转化成 一维数组 对结果无影响
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 利用到 本次和上次 的更新的 f 数组
for(int j=0;j<=m;j++)
{ // 不选第 i 个物品,直接继承上次的更新的结果无需变化
// 选第 i 个物品,更新 f 数组
if(j>=v[i])
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m];
return 0;
}
// 终极版本 时间复杂度:Θ(V∗N) 空间复杂度:Θ(V)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++)
{ // 利用到 本次和上次 的更新的 f 数组
// 由 一次优化 得,直接从 v[i] 更新即可
for(int j=v[i];j<=m;j++)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m];
return 0;
}
多重背包
有
N
N
N 种物品和一个容量是
V
V
V 的背包。
第
i
i
i 种物品最多有
s
i
s_i
si 件,每件体积是
v
i
v_i
vi,价值是
w
i
w_i
wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,
N
,
V
N,V
N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有
N
N
N 行,每行三个整数
v
i
,
w
i
,
s
i
v_i, w_i, s_i
vi,wi,si,用空格隔开,分别表示第
i
i
i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
1.
0
<
N
,
V
≤
100
0 \lt N, V \le 100
0<N,V≤100
0
<
v
i
,
w
i
,
s
i
≤
100
0 \lt v_i, w_i, s_i \le 100
0<vi,wi,si≤100
0
<
N
≤
1000
0 \lt N \le 1000
0<N≤1000
0
<
V
≤
2000
0 \lt V \le 2000
0<V≤2000
0
<
v
i
,
w
i
,
s
i
≤
2000
0 \lt v_i, w_i, s_i \le 2000
0<vi,wi,si≤2000
-
0
<
N
≤
1000
0 \lt N \le 1000
0<N≤1000
0 < V ≤ 20000 0 \lt V \le 20000 0<V≤20000
0 < v i , w i , s i ≤ 20000 0 \lt v_i, w_i, s_i \le 20000 0<vi,wi,si≤20000
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
代码
// 对应 数据1 暴力法,直接枚举每种物品对应的选择 0~s[i] 次,01背包的思路
// 时间复杂度:Θ(V∗∑s[i])
#include<bits/stdc++.h>
using namespace std;
int f[1010][1010],v[1010],w[1010],s[1010];
int main()
{
int n,m;cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
{
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m];
return 0;
}
// 对应 数据2 二进制优化(倍增式优化)
// 时间复杂度Θ (N∗log(s)∗V)
// 任意非负数都可以用 二进制 的表示,(简单解释,十进制数能转化成二进制数)
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m;
int f[N];
int v[N],w[N],cnt;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int a,b,s;cin>>a>>b>>s;
int t=1;
// 将每种情况的 2的幂次方 倍造成新的数据,多出的直接也是造成新的数据
// 多出的 1 2 4 8 ... 2^x s-2^x
while(t<=s)
{
cnt++;
v[cnt]=a*t;
w[cnt]=b*t;
s-=t;
t*=2;
}
if(s>0)
{
cnt++;
v[cnt]=a*s;
w[cnt]=b*s;
}
}
// 重新定义新的 物品种类
n=cnt;
// 01背包
for(int i=1;i<=n;i++)
{
for(int j=m;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m];
return 0;
}
// 对应 数据3 终极版本
// 时间复杂度为Θ(V∗N)
// 利用单调队列
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m;
int f[N],g[N],q[N];
int main()
{
cin>>n>>m;
for(int i = 0; i < n; i++ )
{
int v, w, s;
cin >> v >> w >> s;
memcpy(g, f, sizeof f);
for(int j = 0; j < v; j++) // 余数
{
int hh=0,tt=-1;
for(int k=j;k<=m;k+=v)
{
// 维护队列元素的个数,如果不能继续入队,弹出队头元素
if(hh<=tt &&q[hh]<k-s*v)
hh++;
// 更新最大值
if(hh<=tt)
f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);
// 维护队列的单调性
while(hh<=tt&&g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w)
tt--;
// 当前元素入队
q[++tt]=k;
}
}
}
cout<<f[m];
return 0;
}
混合背包
有
N
N
N 种物品和一个容量是
V
V
V 的背包。
物品一共有三类:
- 第一类物品只能用1次(01背包);
- 第二类物品可以用无限次(完全背包);
- 第三类物品最多只能用
s
i
s_i
si 次(多重背包);
每种体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数, N , V N,V N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N N N 行,每行三个整数 v i , w i , s i v_i, w_i, s_i vi,wi,si,用空格隔开,分别表示第 i i i 种物品的体积、价值和数量。 - s i = − 1 s_i = -1 si=−1 表示第 i i i 种物品只能用1次;
- s i = 0 s_i = 0 si=0 表示第 i i i 种物品可以用无限次;
-
s
i
>
0
s_i >0
si>0 表示第
i
i
i 种物品可以使用
s
i
s_i
si 次;
输出格式
输出一个整数,表示最大价值。
数据范围
0 < N , V ≤ 1000 0 \lt N, V \le 1000 0<N,V≤1000
0 < v i , w i ≤ 1000 0 \lt v_i, w_i \le 1000 0<vi,wi≤1000
− 1 ≤ s i ≤ 1000 -1 \le s_i \le 1000 −1≤si≤1000
输入样例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出样例
8
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m;
int f[N];
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
int v,w,s;cin>>v>>w>>s;
if(s==0) // 01背包
{
for(int j=v;j<=m;j++)
f[j]=max(f[j],f[j-v]+w);
}
else
{ // 二进制转化成01背包
if(s==-1) s=1;
for(int k=1;k<=s;k*=2)
{
for(int j=m;j>=k*v;j--)
f[j]=max(f[j],f[j-k*v]+k*w);
s-=k;
}
if(s)
{
for(int j=m;j>=s*v;j--)
f[j]=max(f[j],f[j-s*v]+s*w);
}
}
}
cout<<f[m];
return 0;
}
二维费用的背包问题
有 N N N 件物品和一个容量是 V V V 的背包,背包能承受的最大重量是 M M M。
每件物品只能用一次。体积是 v i v_i vi,重量是 m i m_i mi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
输入格式
第一行三个整数, N , V , M N,V, M N,V,M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 N N N 行,每行三个整数 v i , m i , w i v_i, m_i, w_i vi,mi,wi,用空格隔开,分别表示第 i i i 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0
<
N
≤
1000
0 \lt N \le 1000
0<N≤1000
0
<
V
,
M
≤
100
0 \lt V, M \le 100
0<V,M≤100
0
<
v
i
,
m
i
≤
100
0 \lt v_i, m_i \le 100
0<vi,mi≤100
0
<
w
i
≤
1000
0 \lt w_i \le 1000
0<wi≤1000
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例
8
代码
// 本质是 两个体积限制 的01背包
#include<bits/stdc++.h>
using namespace std;
const int N=2020;
int f[N][N];
int n,s,m;
int main()
{
cin>>n>>s>>m;
for(int i=1;i<=n;i++)
{
int v,h,w;cin>>v>>h>>w;
for(int j=s;j>=v;j--)
{
for(int k=m;k>=h;k--)
{
f[j][k]=max(f[j][k],f[j-v][k-h]+w);
}
}
}
cout<<f[s][m];
return 0;
}
分组背包问题
有 N N N 组物品和一个容量是 V V V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是
v
i
j
v_{ij}
vij,价值是
w
i
j
w_{ij}
wij,其中
i
i
i 是组号,
j
j
j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N , V N,V N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N N N 组数据:
- 每组数据第一行有一个整数 S i S_i Si,表示第 i i i 个物品组的物品数量;
- 每组数据接下来有 S i S_i Si 行,每行有两个整数 v i j , w i j v_{ij}, w_{ij} vij,wij,用空格隔开,分别表示第 i i i 个物品组的第 j j j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0
<
N
,
V
≤
100
0 \lt N, V \le 100
0<N,V≤100
0
<
S
i
≤
100
0 \lt S_i \le 100
0<Si≤100
0
<
v
i
j
,
w
i
j
≤
100
0 \lt v_{ij}, w_{ij} \le 100
0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
代码
// 01背包,枚举每组的所有的情况
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int v[N][N],w[N][N],s[N];
int f[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>s[i];
for(int j=0;j<s[i];j++)
{
cin>>v[i][j]>>w[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=m;j>=0;j--)
{
for(int k=0;k<s[i];k++)
{
if(v[i][k]<=j) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
}
}
}
cout<<f[m];
return 0;
}
有依赖的背包问题
有 N N N 个物品和一个容量是 V V V 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
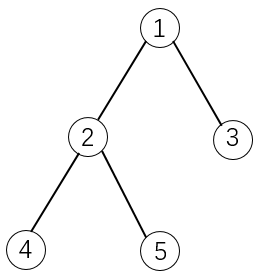
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 i i i,体积是 v i v_i vi,价值是 w i w_i wi,依赖的父节点编号是 p i p_i pi。物品的下标范围是 1 … N 1 … N 1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N , V N,V N,V,用空格隔开,分别表示物品个数和背包容量。
接下来有
N
N
N 行数据,每行数据表示一个物品。
第
i
i
i 行有三个整数
v
i
,
w
i
,
p
i
v_i, w_i, p_i
vi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。
如果
p
i
=
−
1
p_i = -1
pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围
1
≤
N
,
V
≤
100
1 \le N, V \le 100
1≤N,V≤100
1
≤
v
i
,
w
i
≤
100
1 \le v_i, w_i\le 100
1≤vi,wi≤100
父节点编号范围:
- 内部结点: 1 ≤ p i ≤ N 1 \le p_i \le N 1≤pi≤N;
- 根节点 p i = − 1 p_i = -1 pi=−1;
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例
11
代码
// 代码1
// 要求选择子节点必须选择父节点,逆向思路,从根节点开始(因为根节点必须选择)广搜
// 每次都选择 点u ,遍历子节点
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int v[N],w[N];
int h[N],e[N],ne[N],idx;
int f[N][N]; // f[i][j] 以 i点 为子节点,体积不超过 j 的最大值
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
for(int i=h[u];i!=-1;i=ne[i])
{
int son=e[i];
dfs(e[i]); // 遍历子节点
for(int j=m-v[u];j>=0;j--) // m-v[i] 保证选择 当前根节点 u
for(int k=0;k<=j;k++)
f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
}
for(int i=m;i>=v[u];i--) f[u][i]=f[u][i-v[u]]+w[u];
for(int i=0;i<v[u];i++) f[u][i]=0;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h); // 初始化
int root; // 保存根节点
for(int i=1;i<=n;i++)
{
int p;
cin>>v[i]>>w[i]>>p;
if(p==-1) root=i;
else add(p,i);
}
dfs(root); // 广搜所有情况
cout<<f[root][m];
return 0;
}
// 代码2
#include<bits/stdc++.h>
using namespace std;
int f[110][110];//f[u][v]表达选择以 点u 为子树的物品,在体积不超过 v 时所获得的最大价值
vector<int>g[110];
int v[110],w[110];
int n,m,root;
int dfs(int u)
{
for(int i=v[u];i<=m;i++) f[u][i]=w[u];// 点u 必须选,所以初始化f[u][v[u] ~ m]= w[u]
for(int i=0;i<g[u].size();i++)
{
int y=g[u][i];
dfs(y);
for(int j=m;j>=v[u];j--)// j 的范围为v[u]~m, 小于v[u]无法选择以 点u 为子树的物品
{
for(int k=0;k<=j-v[u];k++)//分给子树y的空间不能大于j-v[u],不然都无法选根物品u
{
f[u][j]=max(f[u][j],f[u][j-k]+f[y][k]);
}
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int p;
cin>>v[i]>>w[i]>>p;
if(p==-1)
root=i;
else
g[p].push_back(i);
}
dfs(root);
cout<<f[root][m];
return 0;
}
背包问题求方案数
有 N N N 件物品和一个容量是 V V V 的背包。每件物品只能使用一次。
第 i i i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 1 0 9 + 7 10^9 + 7 109+7 的结果。
输入格式
第一行两个整数, N , V N,V N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i, w_i vi,wi,用空格隔开,分别表示第 i i i 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 1 0 9 + 7 10^9 + 7 109+7 的结果。
数据范围
0
<
N
,
V
≤
1000
0 \lt N, V \le 1000
0<N,V≤1000
0
<
v
i
,
w
i
≤
1000
0\lt v_i, w_i \le 1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例
2
代码
// 根据 01背包 状态转移方程 f[j]=max(f[j],f[j-v]+w)得
// 方案数也随 f[j] 的转移而转移
// 1. f[j-v]+w > f[j] , g[j]=g[j-v]
// 2. f[j-v]+w == f[j], g[j]=( g[j] + g[j-v] )
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int f[1010],g[1010];
int main()
{
int n,m;cin>>n>>m;
fill(g,g+m+1,1); // 初始化 g 数组内元素为 1
for(int i=0;i<n;i++)
{
int v,w;cin>>v>>w;
for(int j=m;j>=v;j--)
{
int va=f[j-v]+w;
if(va>f[j])
{
f[j]=va;
g[j]=g[j-v];
}
else if(va==f[j])
{
g[j]=(g[j]+g[j-v])%mod;
}
}
}
cout<<g[m];
return 0;
}
背包问题求具体方案
有 N N N 件物品和一个容量是 V V V 的背包。每件物品只能使用一次。
第 i i i 件物品的体积是 v i v_i vi,价值是 w i w_i wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1 … N 1 … N 1…N。
输入格式
第一行两个整数, N , V N,V N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N N N 行,每行两个整数 v i , w i v_i, w_i vi,wi,用空格隔开,分别表示第 i i i 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1 … N 1 … N 1…N。
数据范围
0
<
N
,
V
≤
1000
0 \lt N, V \le 1000
0<N,V≤1000
0
<
v
i
,
w
i
≤
1000
0\lt v_i, w_i \le 1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例
1 4
代码
// 逆向思路,输出字典序小的物品编号
// 倒序 01背包,
// 假设存在一个包含第1个物品的最优解,我们一定会选第一个。
// 问题就转化成从2~N这些物品中找到最优解。
#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int f[N][N]; // 二维数组便于求出最后答案
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
// 倒序 01背包
for(int i=n;i>=1;i--)
{
for(int j=0;j<=m;j++)
{
f[i][j]=f[i+1][j];
if(j>=v[i])
f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
}
}
int j=m;
for(int i=1;i<=n;i++)
{
if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])
{
cout<<i<<' ';
j-=v[i]; // 选择第 i 个物品,总体积变小
}
}
return 0;
}



















