描述

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于

2.假设 nums[-1] = nums[n] = −∞

3.对于所有有效的 i 都有 nums[i] != nums[i + 1]

4.你可以使用O(logN)的时间复杂度实现此问题吗？

数据范围：

1≤nums.length≤2×10^5

−2^31<=nums[i]<=2^31−1

如输入[2,4,1,2,7,8,4]时，会形成两个山峰，一个是索引为1，峰值为4的山峰，另一个是索引为5，峰值为8的山峰，如下图所示：

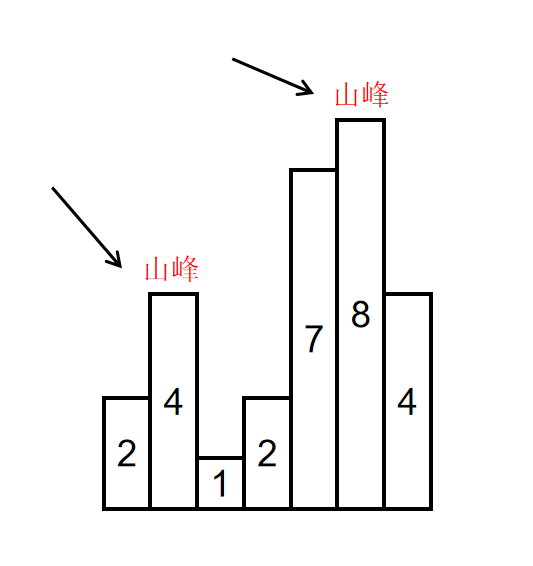
示例1

输入：

[2,4,1,2,7,8,4]

返回值：

1

说明：

4和8都是峰值元素，返回4的索引1或者8的索引5都可以     

示例2

输入：

[1,2,3,1]

返回值：

2

说明：

3 是峰值元素，返回其索引 2  

思路分析：

该题只要找出一个峰值即可，可以使用二分法，判断mid附近的元素来寻找峰值，如果mid右边的元素大于mid的数值，那么峰值可能出现在右半部分，只要将left=mid+1,再判断它右边的元素是否小于它，即可找到峰值；反之mid右边的元素小于mid的数值，那么峰值可能出现在左半部分，只要将right=,再判断它左边的元素。

代码：

import java.util.*;


public class Solution {
    /**
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int findPeakElement (int[] nums) {
        int left=0,right=nums.length-1;
        while(left<right){
            int mid=(left+right)/2;
            //如果mid的下一个元素比它大，则峰值应该产生在mid+1这边
            if(nums[mid]<nums[mid+1]){
                left=mid+1;
            }else{
                right=mid;
            }
            
        }
        return left;
        
    }
}