区块链

AcWing 3285. 区块链 - AcWing

区块链涉及密码学、哈希算法、拜占庭问题、共识算法、故障模型、网络模型等诸多知识，也在金融等领域有广泛的应用。

本题中，我们需要实现一个简单的区块链系统。

在一个分布式网络中，有 nn 个节点通过 mm 条边相连，节点编号从 11 至 nn。

每个节点初始化都有一个相同的“创世块”，链长都为 11。

每个节点在整个过程中都需要维护一条主链，任何操作都只在主链上进行。

在整个系统中产生的每个新块都有唯一的整数编号，创始块的编号为 00，其余块的编号都为正整数。

当某个节点的链更新时，会将它的主链发送给它相邻的节点（邻居）；而当节点收到链时，决定是否更新自己的主链。

下列情况可能会导致某个节点的链更新:

• 某个节点接收到邻居发送过来的链，与当前自己的主链进行比较:
  • 如果接收到的链更长，则将其作为自己的主链:
  • 如果收到的链长度与自身主链相同，且最后一块编号更小，则将其作为自己的主链
  • 如果接收到的链更短，则直接忽略该链。
• 某个节点产生一个新块，将新块放在主链的尾部。

假设网络带宽足够大，每个节点状态更新后，会立刻将自己的主链同时发送给所有邻居。

每个节点在每个时刻总是先接收链，再产生新块（注意这与实际的区块链工作方式不相同）。

每个节点发送、接收、产生块不消耗时间，只有在网络中传输链会消耗时间。

不过因为一些故障，这个网络可能会出现“分区”的情况，即出现多个子网络，不同子网络的节点无法互相收发消息。

在计算机中常用逻辑时钟来定义“时刻”。

逻辑时钟初始时间为 00，以单位 11 递增。

任意节点传输一条链到其邻居所花费的时间相同，都为 tt。

现在已知整个网络的结构以及每个节点产生新块的时间，需要查询特定时刻某个节点的主链。

输入格式

第一行两个正整数分别为 n,mn,m，分别表示网络的 nn 个节点和 mm 条边。

接下来 mm 行，每行 22 个正整数 ui,vi(1≤i≤m)ui,vi(1≤i≤m)，表示网络中节点 uiui 和节点 vivi 具有（双向）连接。

接下来一行两个正整数 t,kt,k，分别表示每次传输延时 tt 和操作（产生块或查询）的数量。

接下来 kk 行，每行 22 或 33 个正整数:

• 如果是三个数 ai,bi,ciai,bi,ci，表示节点 aiai 在 bibi 时刻产生了一个编号为 cici 的块。保证 bi≤bi+1(1≤i<k)bi≤bi+1(1≤i<k)。
• 如果是两个数 ai,biai,bi，表示查询节点 aiai 处理完 bibi 时刻及以前的所有操作后的主链。保证对于同一时刻，任何查询在输入文件中都出现在当前时刻所有的新块被产生之后。

输出格式

依次输出若干行，分别对应每一次查询。

每行第一个正整数 LL 表示主链的长度，接下来 LL 个数表示主链每个块的编号。从链头（一定为 00）到链尾依次输出。

数据范围

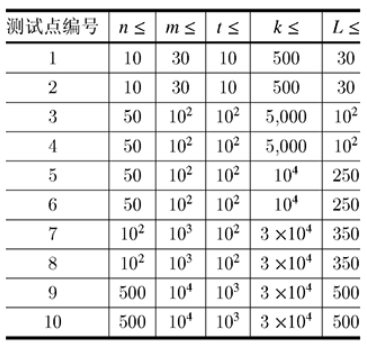
保证题中所有输入均为整数，并且所有整数绝对值不大于 109109。
保证无重边，但可能存在自环。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <sstream>
#include <vector>
#include <queue>

using namespace std;

typedef vector<int> VI;
const int N = 510, M = 20010;

int n, m, w, Q;
int h[N], e[M], ne[M], idx;
vector<VI> g;
int node[N];

struct Op
{
    int t, id, pid, hid;
    bool operator< (const Op& r) const
    {
        return t > r.t;
    }
};
priority_queue<Op> heap;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void eval()
{
    auto t = heap.top();
    heap.pop();

    auto &a = g[node[t.id]], &b = g[t.hid];
    if (b.size() > a.size() || b.size() == a.size() && b.back() < a.back())
    {
        node[t.id] = t.hid;
        for (int i = h[t.id]; ~i; i = ne[i])
            if (e[i] != t.pid && e[i] != t.id)
                heap.push({t.t + w, e[i], t.id, t.hid});
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    g.push_back({0});
    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    scanf("%d%d", &w, &Q);
    getchar();
    char str[100];
    while (Q -- )
    {
        fgets(str, 100, stdin);
        stringstream ssin(str);
        int a[3], cnt = 0;
        while (ssin >> a[cnt]) cnt ++ ;
        if (cnt == 3)
        {
            while (heap.size() && heap.top().t <= a[1]) eval();
            g.push_back(g[node[a[0]]]);
            g.back().push_back(a[2]);
            node[a[0]] = g.size() - 1;
            for (int i = h[a[0]]; ~i; i = ne[i])
                if (e[i] != a[0])
                    heap.push({a[1] + w, e[i], a[0], node[a[0]]});
        }
        else
        {
            while (heap.size() && heap.top().t <= a[1]) eval();
            printf("%d ", g[node[a[0]]].size());
            for (auto x: g[node[a[0]]])
                printf("%d ", x);
            puts("");
        }
    }
    return 0;
}