遗传算法与深度学习实战（4）——遗传算法详解与实现

- 0. 前言
- 1. 遗传算法简介
- - 1.1 遗传学和减数分裂
  - 1.2 类比达尔文进化论
- 2. 遗传算法的基本流程
- - 2.1 创建初始种群
  - 2.2 计算适应度
  - 2.3 选择、交叉和变异
  - 2.4算法终止条件
- 3. 使用 Python 实现遗传算法
- - 3.1 构建种群
  - 3.2 评估适应度
  - 3.3 应用选择
  - 3.4 应用交叉
  - 3.5 应用突变
  - 3.6 运行演化过程
- 小结
- 系列链接

0. 前言

遗传算法是通过代码模拟生命的过程，借鉴了进化、自然选择和通过基因传递成功特征的理念。算法模拟了高级有机繁殖中的减数分裂，我们不必精通遗传学才能使用遗传算法，但了解遗传学能够帮助我们更好的理解遗传算法。在本节中，我们首先回顾遗传学和减数分裂过程的一些重要概念，旨在为代码模拟遗传理论和减数分裂奠定基础，然后使用 Python 实现遗传算法。

1. 遗传算法简介

1.1 遗传学和减数分裂

遗传算法 (Genetic Algorithms, GA) 模拟了遗传水平上生命的演化。同时，在基因过程(减数分裂)中进行了一些简化。当我们谈论遗传学时，需要从脱氧核糖核酸 (DeoxyriboNucleic Acid, DNA) 开始。DNA 链常被称为生命的蓝图，地球生物的一切组成(包括细胞)都由 DNA 定义。
DNA 本身由四对碱基组成，并排列成不同的复杂模式。下图显示了 DNA 是如何形成并缠绕成双螺旋结构，然后折叠成染色体 (Chromosome) 的，染色体位于每个细胞 (Cell) 的细胞核 (Nucleus ) 中。

细胞结构

基因 (Gene) 可以在 DNA 水平上识别，是一段定义生物特征或属性的 DNA 序列。当前，人类基因组计划已经研究和分类了人类染色体中的所有基因。
染色体是这些基因序列的容器，一个单独的染色体可能包含数百个或数千个基因。每个基因本身可能由数百到数千个 DNA 碱基对组成。但在遗传算法中，我们只需要关注基因和染色体。
遗传演化的模拟本身是通过模仿减数分裂的过程来完成的，减数分裂是通过精子和卵子进行细胞繁殖的过程，而有丝分裂是细胞基本分裂的过程。
减数分裂是将一个生物体的一半遗传物质与另一个生物体的一半遗传物质相结合的过程。例如在人类中，男性将其一半的 DNA (精子细胞)与女性的一半 DNA (卵子)相结合。
减数分裂过程如下所示，其中来自父代生物的染色体被组合在一起。在这个过程中，同源染色体对(即相似的染色体)首先对齐，然后发生交叉，即基因物质的共享，重新组合后的染色体用于定义新的生物体。

减数分裂过程

在遗传算法中，主要模拟细胞水平上的基因、染色体和交叉过程等。

1.2 类比达尔文进化论

1.2.1 达尔文进化理论

遗传算法是类比自然界的达尔文进化实现的简化版本。达尔文进化论的原理概括总结如下：

突变：种群中单个样本的特征(也称性状或属性)可能会有所不同，这导致了样本彼此之间有一定程度的差异
遗传：某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性
选择：种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势，因此会产生更多的后代

换句话说，进化维持了种群中个体样本彼此不同。那些适应环境的个体更有可能生存，繁殖并将其性状传给下一代。这样，随着世代的更迭，物种变得更加适应其生存环境。而进化的重要推动因素是交叉 (crossover) 或重组 (recombination) 或杂交——结合双亲的特征产生后代。交叉有助于维持人口的多样性，并随着时间的推移将更好的特征融合在一起。此外，变异 (mutations) 或突变(特征的随机变异)可以通过引入偶然性的变化而在进化中发挥重要作用。

1.2.2 遗传算法对应概念

遗传算法试图找到给定问题的最佳解。达尔文进化论保留了种群的个体性状，而遗传算法则保留了针对给定问题的候选解集合（也称为individuals）。这些候选解经过迭代评估 (evaluate)，用于创建下一代解。更优的解有更大的机会被选择，并将其特征传递给下一代候选解集合。这样，随着世代更新，候选解集合可以更好地解决当前的问题。

基因型 (Genotype)：在自然界中，通过基因型表征繁殖，繁殖和突变，基因型是组成染色体的一组基因的集合。在遗传算法中，每个个体都由代表基因集合的染色体构成。例如，一条染色体可以表示为二进制串，其中每个位代表一个基因。

染色体

种群 (Population)：遗传算法保持大量的个体 (individuals)——针对当前问题的候选解集合。由于每个个体都由染色体表示，因此这些种族的个体可以看作是染色体集合。

候选解集合

适应度函数 (Fitness function)：在算法的每次迭代中，使用适应度函数(也称为目标函数)对个体进行评估。目标函数是用于优化的函数或试图解决的问题。适应度得分更高的个体代表了更好的解，其更有可能被选择繁殖并且其性状会在下一代中得到表现。随着遗传算法的进行，解的质量会提高，适应度会增加，一旦找到具有令人满意的适应度值的解，终止遗传算法。
选择 (Selection)：在计算出种群中每个个体的适应度后，使用选择过程来确定种群中的哪个个体将用于繁殖并产生下一代，具有较高值的个体更有可能被选中，并将其遗传物质传递给下一代。仍然有机会选择低适应度值的个体，但概率较低。这样，就不会完全摒弃其遗传物质。
交叉 (Crossover)：为了创建一对新个体，通常将从当前代中选择的双亲样本的部分染色体互换(交叉)，以创建代表后代的两个新染色体。此操作称为交叉或重组：

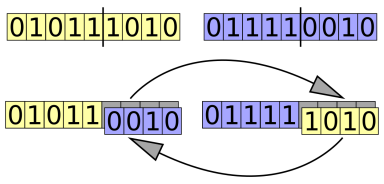
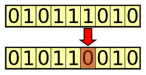
突变 (Mutation)：突变操作的目的是定期随机更新种群，将新模式引入染色体，并鼓励在解空间的未知区域中进行搜索。突变可能表现为基因的随机变化。变异是通过随机改变一个或多个染色体值来实现的。例如，翻转二进制串中的一位：

2. 遗传算法的基本流程

以下流程图显示了基本遗传算法流程的主要阶段：

2.1 创建初始种群

初始种群是随机选择的一组有效候选解(个体)。由于遗传算法使用染色体代表每个个体，因此初始种群实际上是一组染色体。

2.2 计算适应度

适应度函数的值是针对每个个体计算的。对于初始种群，此操作将执行一次，然后在应用选择、交叉和突变的遗传算子后，再对每个新一代进行。由于每个个体的适应度独立于其他个体，因此可以并行计算。
由于适应度计算之后的选择阶段通常认为适应度得分较高的个体是更好的解决方案，因此遗传算法专注于寻找适应度得分的最大值。如果是需要最小值的问题，则适应度计算应将原始值取反，例如，将其乘以值 (-1)。

2.3 选择、交叉和变异

将选择，交叉和突变的遗传算子应用到种群中，就产生了新一代，该新一代基于当前代中较好的个体。
选择 (selection) 操作负责当前种群中选择有优势的个体。
交叉 (crossover，或重组，recombination) 操作从选定的个体创建后代。这通常是通过两个被选定的个体互换他们染色体的一部分以创建代表后代的两个新染色体来完成的。
变异 (mutation) 操作可以将每个新创建个体的一个或多个染色体值(基因)随机进行变化。突变通常以非常低的概率发生。

2.4算法终止条件

在确定算法是否可以停止时，可能有多种条件可以用于检查。两种最常用的停止条件是：

已达到最大世代数。这也用于限制算法消耗的运行时间和计算资源。
在过去的几代中，个体没有明显的改进。这可以通过存储每一代获得的最佳适应度值，然后将当前的最佳值与预定的几代之前获得的最佳值进行比较来实现。如果差异小于某个阈值，则算法可以停止。

其他停止条件：

自算法过程开始以来已经超过预定时间。
消耗了一定的成本或预算，例如 CPU 时间或内存。
最好的解已接管了一部分种群，该部分大于预设的阈值。

3. 使用 Python 实现遗传算法

遗传算法的核心是基因，它描述了一个个体所拥有的各种特征。在遗传算法中，我们将个体视为包含在染色体中的一个或多个基因序列。我们也可以模拟多个染色体，但通常只需使用一个染色体。
种群中的每个个体都有一个包含基因序列的染色体。每个基因由一个数字或布尔值描述，当然一个基因可以包含任何信息，包括文本字符、颜色或任何用于描述个体特征的信息。一个基因可以映射到单个数值，也可以由多个值定义。同样，我们可以定义一个单独的染色体，也可以定义多个染色体。

3.1 构建种群

为了便于理解，在本节中，我们将通过 Python 实现一个简单的遗传算法。
首先，使用 NumPy 数组设置一个种群。种群中的每个个体都由一个大小为 genes 的一维向量组成。将整个种群使用 randint 函数构建成一个元素值为 0 或 1 的 NumPy 张量，并且张量的大小为 (population, genes) 。得到的输出张量中每一行表示一个大小为 genes 的向量：

import numpy as np
import random
import matplotlib.pyplot as plt

#initial population
population = 100
genes = 100
generations = 100

pop = np.random.randint(0,2, size=(population,genes))
print(pop)

3.2 评估适应度

在一个种群中，我们需要确定哪个是最适合或最有可能解决问题的个体。在本节的简单示例中，我们的目标是进化个体，使其所有基因的值都为 1。这个问题在遗传算法中称为 OneMax 问题，是常见的入门问题之一。
为了确定个体的适应度，我们通常会推导出一个适应度函数用于计算个体接近目标的程度。通常，该目标是最大化或最小化目标值。在 OneMax 问题中，我们的目标是最大化个体中所有基因的总和。由于每个基因的元素取值是 0 或 1，最大化总和意味着个体的所有基因都为 1。
在 NumPy 中，指定参数种群张量 pop 和轴 axis=1 调用 np.sum 函数计算适应度：

fitness = np.sum(pop,axis=1)
plt.hist(fitness)

下图显示了随机初始化的种群中个体适应度的直方图，输出近似一个大约以 50 中心的正态分布。在本例中，由于每个个体只有一个包含 100 个基因的染色体，每个基因的值为 0 或 1，因此最大适应度为 100。

适应度评估

3.3 应用选择

在评估种群的适应度之后，我们可以确定哪些个体用于繁殖以产生后代。在自然界中，通常强壮或适应性更强的个体能够生存和繁殖，使后代共享部分遗传基因。在遗传算法中，我们通过确定种群中哪些个体适合繁殖来模拟这个过程。我们可以使用不同策略来进行选择，但对于本节的简单示例，我们选择适应度最高的两个个体作为整个下一代的父母，这种选择方式称为精英选择。
elite_selection 函数以种群适应度作为输入，通过使用 argsort 函数对适应度值进行排序，返回适应度最高的两个个体的索引，返回的索引可以用于通过 pop[parents[idx]] 从种群中提取个体：

def elite_selection(fitness):
    return fitness.argsort()[-2:][::-1]  

parents = elite_selection(fitness)
print(pop[parents[0]])

输出结果

对于本节中的简单示例，选择最佳个体进行繁殖能够得到不错的效果，但在更复杂的问题中，通常使用更多样化的选择方法。父母选择的多样性使个体可能传播在短期内并不有利的特征，但有可能成为最终的解决方案，避免在求解过程中陷入局部最大/小值的情况。

3.4 应用交叉

在选择了父母之后，可以应用交叉或者说是繁殖过程来创建后代。类似于生物学中的细胞分裂过程，通过交叉操作模拟染色体的组合，其中双亲中的每一个都共享其基因序列的一部分，并进行组合。
在交叉操作中，可以随机选择一个或多个点或使用某种策略沿着基因序列选择一个或多个点。在所选择的点上分割双亲的基因序列然后重新组合。在本节示例中，我们并未考虑每个后代与双亲共享基因序列的百分比。对于需要数万甚至数百万代进化的复杂问题，我们需要更平衡的交叉策略，而非随机交叉策略。
在代码实现中，交叉操作首先复制父代以创建原始子代，然后使用变量 crossover_rate 随机确定是否进行交叉操作。如果进行交叉操作，则沿基因序列生成一个随机点作为交叉点，用来分割基因序列，然后通过组合双亲的基因序列生成子代：

def crossover(parent1, parent2, crossover_rate):
    # children are copies of parents by default
    child1, child2 = parent1.copy(), parent2.copy()  
    # check for recombination
    if random.random() < crossover_rate:
        # select crossover point that is not on the end of the string
        pt = random.randint(1, len(parent1)-2)
        # perform crossover    
        child1 = np.concatenate((parent1[:pt], parent2[pt:]))
        child2 = np.concatenate((parent2[:pt], parent1[pt:]))
    return [child1, child2]

crossover(pop[parents[0]],pop[parents[1]], .5)

输出结果

交叉操作有多种不同的变体和应用方式。在本节中，选择一个随机的交叉点，然后在交叉点处组合序列。但在某些情况下，只有符合特定规则的基因序列才是有效的，对于这类情况，我们需要其他方法来保持基因序列的完整性。

3.5 应用突变

在自然界中，有时会看到后代拥有父母都不具备的特征，这是由于后代可能会发生突变，导致出现了父母没有的特征。随着时间的推移，这些突变可能会不断积累，从而产生全新的特征或物种。通常认为，通过突变这个关键过程，生命才得以从单细胞生物进化为高级物种。
在进化过程中，突变通常是独特且罕见的。在遗传算法中，可以在交叉操作之后使用指定突变规律和突变类型应用突变操作。因此，可以将突变理解为在繁殖过程中可能发生的基因变化现象。
在本节中，我们通过翻转序列中的一个位(基因)执行突变操作。在 mutation 函数中，测试每个个体的每个基因是否存在突变的可能性。为了测试该函数，我们使用 50% 的mutation_rate进行对比，但通常突变率需要设置为较小，一般小于 5％：

def mutation(individual, mutation_rate):
    for i in range(len(individual)):
        # check for a mutation
        if random.random() < mutation_rate:
            # flip the bit
            individual[i] = 1 - individual[i]
    return individual

mutation(pop[parents[0]], .5)

输出结果

与选择和交叉操作一样，突变也具有多种类型。在某些情况下，我们可能希望保持突变的可能性较低，而在其他情况下，种群可能会从更高的随机性中受益。突变率就像深度学习 ( Deep learning, DL) 中的学习率一样，较低的学习率会使训练过程更加稳定，但可能会陷入局部最优解，而较高的学习率会的初始结果较好，但可能无法稳定训练。

3.6 运行演化过程

遗传算法从种群的随机初始化开始，接下来，第一步操作是计算所有个体的适应度。根据适应度，使用选择操作确定哪些个体用于繁殖后代。然后应用交叉操作，再应用突变，然后再次计算适应度。接下来，检查是否满足停止标准。通常，通过 GA 运行的代数定义停止标准，其中每代视为一个完整的 GA 过程。我们还可以使用其他停止标准，例如实现最大或最小适应度。
将所有 GA 过程代码放入 simple_GA 函数中。在函数中，通过应用遗传操作产生新的后代，并返回这些后代种群，以便作为下一遗传过程的父代传递给 simple_GA ：

def simple_GA(pop, crossover_rate=.5, mutation_rate=.05):
    fitness = np.sum(pop,axis=1) 
    parents = elite_selection(fitness)
    children = np.zeros((population,genes))  
    for i in range(population):
        offspring = crossover(pop[parents[0]],pop[parents[1]], crossover_rate)
        children[i] = mutation(offspring[0],mutation_rate)  
    return children

simple_GA(pop)

函数 simple_ga 执行了种群的所有遗传操作的一个完整过程，循环调用 simple_ga 函数直到达到算法的停止标准。记录每代种群的适应度，以观察种群的进化过程：

#initial population
pop = np.random.randint(0,2, size=(population,genes))

for i in range(generations):
    pop = simple_GA(pop)
    fitness = np.sum(pop,axis=1)
    plt.hist(fitness)
    plt.show()
    print(f"Generation {i+1}")
    print(f"    Max fitness {np.max(fitness)}")
    print(f"    Min fitness {np.min(fitness)}")
    print(f"    Mean fitness {np.mean(fitness)}")
    print(f"    Std fitness {np.std(fitness)}")

下图展示了种群演化 100 代的结果，可以看到算法结束时最大适应度为 98，最小适应度为 86，平均值为 92.49，标准差为 2。与 DL 不同的是，在 DL 中，重点关注最大/最小损失或准确性，而在 GA 中，重点关注确定整个种群的进化情况。

输出结果

虽然单个个体具有较高适应度可以解决复杂的问题，但我们希望确保整个种群的适应度足够高以继续演化。与 DL 不同，在 DL 中训练效果随时间而衰减，在 GA 中，通常会出现突破性演化，产生根本性变化和更优解。因此，我们通常希望在使用进化算法时考虑整个种群的适应度。
适者生存是进化算法训练的目标，因此我们通常希望看到个体适应度满足正态分布，以确保种群对变化具有适应性，我们可以通过使用不同类型的选择和突变操作来控制适应度的分布。
遗传算法中可以通过调整超参数和遗传算子来优化解的进化，接下来，通过介绍遗传算法中常见超参数及其作用来了解遗传算法性能优化的方法：

种群大小：表示每一代进化模拟的个体数量。种群大小与染色体大小或基因序列长度相关，因此，具有更复杂基因序列的个体需要更大的训练种群才有机会得到高适应度个体
基因/染色体长度：染色体的数量和长度或基因的类型通常由问题设置
世代数：类似于 DL 中的 epoch，世代数表示进化的迭代次数。在遗传算法中，需要进化整个种群，世代数通常由染色体长度和复杂性决定。这可能与种群大小平衡，可以使用大量的种群和少量的世代数
交叉率：用于确定交叉点的位置或数量
突变率：用于确定个体基因发生突变的可能性。较高的突变率通常会导致种群发生较多变异，这可能有利于解决复杂的问题。但是，较高的变异率也可能阻碍个体达到最佳表现。相反，较低的突变率会产生较少的种群变异

通过在代码中修改这些超参数，并观察不同超参数对运行结果的影响，学习和理解如何修改超参数是改变种群演化的最佳方式。遗传算法为进化计算 (Evolutionary Computation, EC) 方法奠定了基础。从根本上讲，进化和适者生存的概念是 EC 方法的关键组成部分。

小结

在遗传算法 (Genetic Algorithms, GA) 中，使用选择、交叉、突变和适应度来模拟生物减数分裂或繁殖的基本操作。适应度是衡量个体优劣的指标，可以用于量化模拟个体成功解决给定问题的能力。通过修改遗传算法超参数，如种群大小、世代数、交叉率和突变率等超参数，能够调整和修改进化进程。在本节中，我们介绍了遗传算法基本概念及算法流程，并使用 Python 实现遗传算法解决 OneMax 问题。