【kruskal】最小生成树算法详解

news2024/11/24 17:31:17

最小生成树kruskal

洛谷 P3366 【模板】最小生成树

算法介绍

最小生成树（Minimum Spanning Tree, MST）是一个无向图中连接所有顶点的边的集合，这个集合满足两点：第一，它是一棵树，即任意两个顶点之间恰好有一条路径；第二，它的总权重（边的权值之和）尽可能小。其中最著名的算法有 Prim 算法和 Kruskal 算法：
- Prim 算法是从图的一个顶点开始，逐步添加与其相邻且尚未加入树中的边，每一步选择当前生成树外边权值最小的边，直到所有顶点都被包含在内。
- Kruskal 算法则将图的所有边按权重从小到大排序，然后依次尝试加入边，如果这条边不会形成环，则加入，直到树包含了所有顶点，这里我们主要使用的就是这个算法。

例题演示

洛谷 P3366 【模板】最小生成树👇

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 $N, M$ ，表示该图共有 $N$ 个结点和 $M$ 条无向边。

接下来 $M$ 行每行包含三个整数 $X_i,Y_i,Z_i$ ，表示有一条长度为 $Z_i$ 的无向边连接结点 $X_i,Y_i$ 。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

样例输入 #1

样例输出 #1

提示

数据规模：

对于 $20\%$ 的数据， $N\le 5$ ， $M\le 20$ 。

对于 $40\%$ 的数据， $N\le 50$ ， $M\le 2500$ 。

对于 $70\%$ 的数据， $N\le 500$ ， $M\le 10^4$ 。

对于 $100\%$ 的数据： $1\le N\le 5000$ ， $1\le M\le 2\times 10^5$ ， $1\le Z_i \le 10^4$ 。

样例解释：

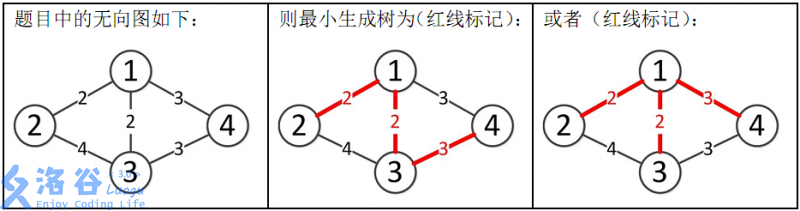
所以最小生成树的总边权为 $2 + 2 + 3 = 7$ 。

代码与讲解

此题是一道非常经典的最小生成树算法，模板中的模板，今年来也应该只会在CSP-J出现，但这道题可以很好的给我们提供一个对kruskal算法的理解与学习。具体步骤如下：

用数组存边，并注意将边权放在第一个参数的位置，以便后期进行字典序排序。
排序，并进入kruskal算法
kruskal算法中，利用了一些并查集的知识（并查集），先将每个点的连接设为自己本身，然后判断每一条边的两个端点是否连在一起，也就是同一条树上，若没连就连上，标记加一，权值累加。

代码演示（含注释）

#include<bits/stdc++.h>
#define fi first
#define se second
#define PII pair<int,pair<int,int>>//数组对，用于存边的各个参数
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)//加快输入输出

using namespace std;

const int N = 1e6+1;


int acc[N],n,m;
PII arr[N];//边的数组

int find(int x)//并查集模板
{
	if(acc[x] != x)		acc[x] = find(acc[x]);
	return acc[x];
}

void kruskal()
{
	int sum  = 0,cnt = 0;
	for(int i = 1;i <= n;i++)	acc[i] = i;//每个点连接自己
	for(int i = 1;i <= m;i++)
	{
		int a = arr[i].se.fi,b = arr[i].se.se,c = arr[i].fi;//取出参数
		if(find(a) != find(b))//若没连上
		{
			acc[find(a)] = find(b);//连起来
			sum += c;//边权累加
			cnt++;//标记加
		}
	}
	if(cnt == n-1)		cout<<sum;//若连边数等于点数-1，说明正好连接完全
	else				cout<<"orz";//不是连通图，输出
}


int main()
{
	IOS;//加快输入输出
	cin>>n>>m;
	for(int i = 1;i <= m;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		arr[i] = {z,{x,y}};//用数组存边，边权放第一个参数
	}
	sort(arr+1,arr+1+m);//排序
	kruskal();//算法
}