2024.8.12

2024.8.12 【梦最让我费解的地方在于，明明你看不清梦里人们的脸，却清晰地知道他们是谁。】

Monday 七月初九

序理论

最小链覆盖&最长反链长度

我们设定一个二元关系符R和一个集合A

我们设定<A,R>这样一个类群，那么对于任意 $a_i\in A,a_j \in A$ , 二元关系式$a_i\ R\ a_j $将返还一个bool值作为结果

在此类群中，我们对二元关系符做如下规定

自反性（reflexive） $(\forall a_i \in A),a_i \ R \ a_i \ = true$
反对称性（antisymmetric） $(\forall a,b \in A),a \ R \ b \ = true \Rightarrow a\ =\ b$
传递性（transitive） $(\forall a,b,c\in A),a\ R \ b\ =true ,b\ R\ c\ =true \Rightarrow a\ R\ c\ = true$

那么对于这个类群的最小链覆盖为
$\subset A,\forall \ x \in B \\ \exists \ y \in B\Rightarrow \\ x\ R\ y\ = true \vee y\ R\ x\ = true$
B为满足条件的最小集

最长反链覆盖为

$\subset A,\forall \ x \in B \\ \forall \ y \in B\Rightarrow \\ \neg (x\ R\ y\ = true \vee y\ R\ x\ = true)$
B为符合条件的最大集

Dilworth 定理

对于一个这样的类集，最小链覆盖是等于最长反链覆盖的

显然，当 $∣ A ∣ <= 3$ 时，一定成立

我们设存在集合 $C$ 使得其满足该定理

使其宽度为K，若 $C$ 中任意元素均不可比，该定理显然成立

否则在该集合中取出一条长度大于1的链，令其中链首为 $m$ ，链尾为 $M$

令 $T=A\setminus\{m,M\}$ ，若 T中的宽度不超过 $d - 1$ ，则由归纳假设知 $T$ 可被至多$ d-1$条链覆盖，进而 $S$ 可被这些链再加上链 ${m,M\}$ 覆盖，命题成立，否则说明 $T$ 中的宽度也为 $d$ ，令 $T$ 中最长的一条反链为 $B$

我们考虑如下两个集合：
$A^+=\{x\in A:(\exists a\in B) \ a \preceq x\}\\ A^-=\{x\in A:(\exists a\in B) \ x \preceq a\}\\$
我们很难不发现
$A^+\sqcup A^- = A\\ A^+\sqcap A^- = B\\ |A^+|<|A|,|A^-|<|A|$
对 $S^+,S^-$ 分别进行数学归纳

那么两个集合最小链覆盖数是 $d$ ，且均包含 $B$ 中一个元素

命题得证

[[ARC165E] Random Isolation]([ARC165E] Random Isolation - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

[ARC165E] Random Isolation

题面翻译

给一棵 $n$ 个节点的树和一个整数 $K$ 。每次操作，等概率随机选一个所在连通块大小大于 $K$ 的点，并删掉这个点和与之相连的所有边。重复操作直到图上所有连通块大小不超过 $K$ ，求期望操作次数，答案对 $998244353$ 取模。

$1\le K < N\le 100$ 。

translated by yxcat.

题目描述

頂点に $ 1 $ から $ N $ の番号が付いた $ N $ 頂点からなる木があります。 $ i $ 番目の辺は頂点 $ A_i,B_i $ を結びます。

グラフの連結成分が含む頂点の数がそれぞれ $ K $ 以下になるまで以下の操作を行い続けます。

$ N $ 個の頂点のうち、$ K+1 $ 個以上の頂点を含む連結成分に属する頂点を $ 1 $ つ一様ランダムに選ぶ。選んだ頂点を端点とする辺をすべて削除する。

操作を行う回数の期待値を $ \bmod\ 998244353 $ で求めてください。

期待値 $ \text{mod\ }{998244353} $ の定義求める期待値は必ず有理数になることが証明できます。また、この問題の制約のもとでは、その値を既約分数 $ \frac{P}{Q} $ で表した時、$ Q\ \not\ \equiv\ 0\ \pmod{998244353} $ となることも証明できます。よって、$ R\ \times\ Q\ \equiv\ P\ \pmod{998244353},\ 0\ \leq\ R\ &lt\ 998244353 $ を満たす整数 $ R $ が一意に定まります。この $ R $ を答えてください。

输入格式

入力は以下の形式で標準入力から与えられます。

$ N $ $ K $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_{N-1} $ $ B_{N-1} $

输出格式

答えを出力してください。

样例 #1

样例输入 #1
4 2
1 2
2 3
2 4
样例输出 #1
249561090
样例 #2

样例输入 #2
20 10
16 8
6 2
18 3
3 12
5 1
13 9
13 19
3 11
5 13
17 6
8 14
1 16
16 20
11 15
3 10
15 4
5 18
1 7
1 17
样例输出 #2
181196154
提示

制約

$ 1\ \leq\ K\ <\ N\ \leq\ 100 $
$ 1\ \leq\ A_i,B_i\ \leq\ N $
与えられるグラフは木
入力される値はすべて整数

Sample Explanation 1

例えば $ 1 $ 回目の操作で頂点 $ 2 $ が選ばれた場合、操作によって全ての辺が削除され、操作後は各連結成分が含む頂点の数はそれぞれ $ 2 $ 以下であるため操作を終了します。一方 $ 1 $ 回目の操作で頂点 $ 1 $ が選ばれた場合、操作後頂点 $ 2,3,4 $ からなる連結成分が残るため、$ 2 $ 回目の操作が行われます。操作回数の期待値は $ \frac{7}{4} $ です。

//2024.8.12
//by white_ice
//[ARC165E] Random Isolation | AT_arc165_e
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define int long long
#define itn long long
constexpr int oo = 105;
constexpr int mod=998244353;
int n,m;
itn siz[oo],f[oo][oo][oo],g[oo][oo];
int c[oo<<1],ic[oo<<1];
struct nod{int to[oo<<1],nxt[oo<<1],head[oo],tot;
__inline void adde(int u,int v){to[++tot]=v,nxt[tot]=head[u],head[u]=tot;}}S;
__inline int qpow(int x,int y){int ans=1;while (y){
    if(y&1)ans=ans*x%mod;y>>=1;x=x*x%mod;}return ans;}
__inline void dfs(int u,int fa){
    siz[u]=1,f[u][1][0]=1;
    for (int i=S.head[u];i;i=S.nxt[i]){
        int v=S.to[i];
        if (v==fa) continue;
        dfs(v,u);
        for (int j=siz[u]+siz[v];j>=0;j--)
            for (int k=siz[u]+siz[v];k>=0;k--)
                g[j][k]=f[u][j][k],f[u][j][k]=0;
        for (int j=siz[u];j>=1;j--)
            for (int k=siz[u]-j;k>=0;k--){
                f[u][j][k+1]=(f[u][j][k+1]+g[j][k])%mod;
                for (int p=siz[v];p>=1;p--)
                    for (int q=siz[v]-p;q>=0;q--){
                        f[u][j+p][k+q]=(f[u][j+p][k+q]+g[j][k]*f[v][p][q]%mod)%mod;
                    }                
            }
        siz[u]+=siz[v];
    }
}
main(void){
	//fre();
	cin.tie(0)->sync_with_stdio(0);
    c[0]=ic[0]=1;
    for (int i=1;i<=200;i++)	
		c[i]=c[i-1]*i%mod;
    ic[200]=qpow(c[200],mod-2);
    for (int i=200-1;i>=1;i--)	
		ic[i]=ic[i+1]*(i+1)%mod;
	cin >> n >> m ;
    for (int u,v,i=1;i<n;i++){
        cin >> u >> v;
        S.adde(u,v),S.adde(v,u);
    }
    dfs(1,0);
    int ans=0;
    for (int u=1;u<=n;u++){
        for (int i=m+1;i<=siz[u];i++){
            for (int j=0;j<=siz[u]-i;j++)
                ans=(ans+f[u][i][j]*c[i]%mod*c[j+(u!=1)]%mod*ic[i+j+(u!=1)]%mod)%mod;//,cout<<u<<" "<<i<<" "<<j<<" "<<f[u][i][j]<<"\n";
        }
    }
    cout << ans <<"\n";
    exit(0);
}

我们考虑，既然是计算概率，

那么对于一棵树，我们不妨将其转化为一个序列来考虑

我们假设一个序列s，我们从这个序列中选出n个点，假设已经从s中选出了x个点，那么又有n-x个点在剩余的序列中选择

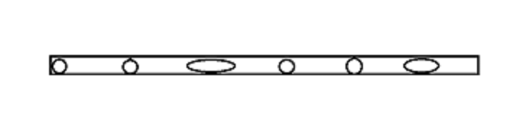
（其中椭圆为要去除的点）

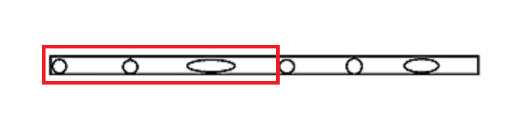
（红色部分为去除的）

那么后面的部分有n-x个点可以被选择，后半部分共k个点

那么我们将k自由组合排序，考虑第一个被选择的点

这些点的选择概率都是 $\frac{1}{n-x}$ ,所以我们考虑组合意义，共 $\frac{(n-x)!(k-n+x)!}{k!}$ 种可能

通过这种转化，我们将求解概率变为了计数问题

那么我们应该考虑如何取出点了

对于一个子树T，|T|>k,对于这个子树，我们一定可以对这一棵子树进行操作

那么我们就可以统计子树大小大于k的个数

那么他的贡献就是T出现的概率我们设T出现的概率是 $p (T)$ ,那么答案的总期望就是 $\sum_{size_T>k}p(T)$

关于这个统计，使用树形DP求解总数即可

设 $f [x] [i] [j]$ 为为 $x$ 子树中选了包含 $x$ 在内的 $i$ 个点，有 $j$ 个点与之相连的方案数，使用背包转移即可

[P3974 [TJOI2015] 组合数学]([P3974 TJOI2015] 组合数学 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))

[TJOI2015] 组合数学

题目描述

为了提高智商，ZJY 开始学习组合数学。某一天她解决了这样一个问题：给一个网格图，其中某些格子有财宝。每次从左上角出发，只能往右或下走。问至少要走几次才可能把财宝全捡完。

但是她还不知足，想到了这个问题的一个变形：假设每个格子中有好多块财宝，而每一次经过一个格子至多只能捡走一块财宝，其他条件不变，至少要走几次才可能把财宝全捡完？

这次她不会做了，你能帮帮她吗？

输入格式

第一行为一个正整数 $t$ ，表示数据组数。

每组数据的第一行是两个正整数 $n$ 和 $m$ ，表示这个网格图有 $n$ 行 $m$ 列。

接下来 $n$ 行，每行 $m$ 个非负整数，表示这个格子中的财宝数量（ $0$ 表示没有财宝）。

输出格式

对于每组数据，输出一个整数，表示至少走的次数。

样例 #1

样例输入 #1
1
3 3
0 1 5
5 0 0
1 0 0
样例输出 #1
10
提示

数据范围

对于 $30\%$ 的数据， $\le 5$ ， $\le 5$ ，每个格子中的财宝数不超过 $5$ 块。

对于 $50\%$ 的数据， $\le 100$ ， $\le 100$ ，每个格子中的财宝数不超过 $1000$ 块。

对于 $100\%$ 的数据， $1\le t\le 2$ ， $1\le n \le 1000$ ， $1\le m \le 1000$ ，每个格子中的财宝不超过 $10^6$ 块。

//2024.8.12
//by white_ice
//[TJOI2015] 组合数学 | P3974
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 1003;
itn n,m;itn st[oo][oo];
int f[oo][oo];
main(void){
    //fre();
    cin.tie(0)->sync_with_stdio(0);
    itn t;cin >> t;
while (t--){
    memset(f,0,sizeof(f));
    cin >> n >> m;
    for (itn i=1;i<=n;i++)for (int j=1;j<=m;j++)cin >> st[i][j];
    for (itn i=1;i<=n;i++)for (itn j=m;j>=1;j--){
        f[i][j] = max(f[i-1][j],f[i][j+1]);
        f[i][j] = max(f[i-1][j+1]+st[i][j],f[i][j]);
    }
    cout << f[n][1] << '\n';
}
    cout << flush;
    exit (0);
}