假设一个二叉树上各结点的权值互不相同。

我们就可以通过其后序遍历和中序遍历来确定唯一二叉树。

请你输出该二叉树的 ZZ 字形遍历序列----也就是说，从根结点开始，逐层遍历，第一层从右到左遍历，第二层从左到右遍历，第三层从右到左遍历，以此类推。

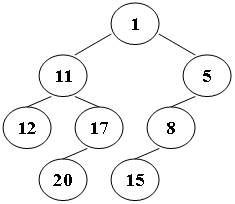
例如，下图所示二叉树，其 ZZ 字形遍历序列应该为：1 11 5 8 17 12 20 15。

输入格式

第一行包含整数 NN，表示二叉树结点数量。

第二行包含 NN 个整数，表示二叉树的中序遍历序列。

第三行包含 NN 个整数，表示二叉树的后序遍历序列。

输出格式

输出二叉树的 ZZ 字形遍历序列。

数据范围

1≤N≤301≤N≤30

输入样例：

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

输出样例：

1 11 5 8 17 12 20 15

#include <iostream>
#include <cstring>
#include <map>
#include <queue>
#include <algorithm>
#include <vector>
using namespace std;
const int N=40;
int inorder[N],postorder[N];
int n;
int depth[N];
map<int,int>l,r,pos;    vector<int>res;
int  build(int il,int ir,int pl,int pr)
{
    if(il>ir)    return 0 ;
    int root=postorder[pr];    

    int k=pos[root];
     if(il<k)   l[root]=build(il,k-1,pl,pl+k-1-il); 
    if(ir>k)    r[root]=build(k+1,ir,pl+k-il,pr-1);
	// cout<<root<<" "<< l[root]<<" "<<r[root]<<endl;
	return root;
}

void bfs(int root)
{  
    

    queue<int>q;
    q.push(root);
    int st=1;
  int flag=0;
    while(!q.empty())
    {
        int size=q.size();
        
            for(int i=0;i<size;i++)
            {
                auto t=q.front();
                res.push_back(t);
                q.pop();
                if(l[t])    q.push(l[t]);
                if(r[t])    q.push(r[t]);
                
                
            }
            if(!flag)    reverse(res.begin()+res.size()-size,res.end());
        flag=!flag;
            
        
        
        
    }
}
int main()
{
    
    cin>>n;
    // memset(l,-1,sizeof(l));
    // memset(r,-1,sizeof(r));
    for(int i=0;i<n;i++)    cin>>inorder[i],pos[inorder[i]]=i;
    for(int i=0;i<n;i++)    cin>>postorder[i];
    
   int root= build(0,n-1,0,n-1);
   bfs(root);
    // int root=postorder[n-1];
    cout<<res[0];
    for(int i=1;i<n;i++)    cout<<" "<<res[i];
}