文章目录
- 一、实验目的
- 二、实验内容与原理(简单列了一下提纲)
- 第一部分:连续系统时域响应MATLAB仿真分析
- 第二部分:连续系统时域响应Multisim电路仿真分析
- 三、实验器材
- 四、实验步骤
- 第一部分:连续系统时域响应MATLAB仿真分析
- (一)验证性实验
- (二)程序设计实验
- 第二部分:连续系统时域响应Multisim电路仿真分析
- 五、实验数据及结果分析
- 第一部分:连续系统时域响应MATLAB仿真分析
- 第二部分:连续系统时域响应Multisim电路仿真分析
- 1.无阻尼
- 2.欠阻尼
- 3.临界阻尼
- 4.过阻尼
- 5.二阶不稳定系统
- 六、实验结论
- 七、思考题
- 八、其他
一、实验目的
1.熟悉LTI系统零输入响应与零状态响应的概念及其叠加性。
2.理解和掌握LTI连续系统阶跃响应与冲激响应的概念,了解其测试原理和测试方法。
3.理解和掌握动态系统模型参数的变化对系统时域响应的影响。
4.熟悉Multisim软件的使用方法。
5.熟悉MATLAB软件的使用方法。
二、实验内容与原理(简单列了一下提纲)
第一部分:连续系统时域响应MATLAB仿真分析
(一)实验内容
1. 采用MATLAB实现连续时间信号的卷积积分运算(求系统的零状态响应)。
2. 采用 step()、impulse()两函数编程,实现连续LTI系统的单位阶跃响应和单位冲激响应。
3. 采用MATLAB求连续LTI系统的零输入响应。
(二)实验原理
1. 连续时间信号卷积积分的数值计算
2. impulse()函数和step()函数的调用格式
3. 求解连续LTI系统零输入响应的理论知识
第二部分:连续系统时域响应Multisim电路仿真分析
(一)实验内容
1.大惯量二阶LTI连续系统零输入响应、零状态响应的测试与分析。
2.分别测试二阶LTI连续系统在欠阻尼、临界阻尼、过阻尼、不稳定等条件下的阶跃响应与冲激响应,比较不同状态下阶跃响应与冲激响应的区别,分析LTI系统模型参数与特征根的对应关系及其对系统时域响应的影响。
(二)实验原理及电路说明
1.连续系统时域响应分析电路
2.系统的工作状态: ξ=0(无阻尼); ξ>1(过阻尼); ξ=1(临界阻尼); 0<ξ<1(欠阻尼);ξ <0(不稳定)
三、实验器材
一台PC机(自备)
Multisim软件(2011及以上版本,自备)
MATLAB 2014a及以上版本(自备)
四、实验步骤
第一部分:连续系统时域响应MATLAB仿真分析
(一)验证性实验
1. 连续时间信号的卷积积分(零状态响应)
2. 连续系统的单位阶跃响应和单位冲激响应
(二)程序设计实验
参照上述例题,根据下列实验内容要求,设计出完整程序,并给出程序流程图。
1. 已知连续LTI系统,激励 ,单位冲激响应 ,试绘出系统零状态响应 的波形。
2. 已知LTI系统,激励 ,单位冲激响应 ,试给出系统零状态响应 的数学表达式。
3. 试分别绘出下列微分方程描述的LTI系统单位冲激响应和阶跃响应的波形,并求出相应的数值解。
(
1
)
2
y
′
′
(
t
)
+
y
′
(
t
)
+
8
y
(
t
)
=
f
(
t
)
(1) 2y''(t)+y'(t)+8y(t)=f(t)
(1)2y′′(t)+y′(t)+8y(t)=f(t)
(
2
)
3
y
′
′
′
(
t
)
+
2
y
′
(
t
)
−
4
y
(
t
)
=
2
f
′
(
t
)
+
f
(
t
)
(2) 3y'''(t)+2y'(t)-4y(t)=2f'(t)+f(t)
(2)3y′′′(t)+2y′(t)−4y(t)=2f′(t)+f(t)
(
3
)
y
′
′
(
t
)
+
2
y
′
(
t
)
+
5
y
(
t
)
=
4
f
′
(
t
)
(3) y''(t)+2y'(t)+5y(t)=4f'(t)
(3)y′′(t)+2y′(t)+5y(t)=4f′(t)
4. 已知连续LTI系统,微分方程为
3
y
′
′
′
(
t
)
+
5
y
′
′
(
t
)
+
7
y
′
(
t
)
+
y
(
t
)
=
2
f
′
(
t
)
+
f
(
t
)
3y'''(t)+5y''(t)+7y'(t)+y(t)=2f'(t)+f(t)
3y′′′(t)+5y′′(t)+7y′(t)+y(t)=2f′(t)+f(t) ,试分别绘出在下列给定初始条件下,系统零输入响应的波形。
(
1
)
y
(
0
−
)
=
2
,
y
′
(
0
−
)
=
1
,
y
″
(
0
−
)
=
0
(1) y(0_-)=2 ,y' (0_-)=1 ,y″ (0_-)=0
(1)y(0−)=2 ,y′(0−)=1 ,y″(0−)=0
(
2
)
y
(
0
−
)
=
1
,
y
′
(
0
−
)
=
0
,
y
″
(
0
−
)
=
1
(2) y(0_-)=1 ,y' (0_-)=0 ,y″ (0_-)=1
(2)y(0−)=1 ,y′(0−)=0 ,y″(0−)=1
5. 已知连续LTI系统,微分方程为
y
″
(
t
)
+
5
y
′
(
t
)
+
6
y
(
t
)
=
4
f
′
(
t
)
+
7
f
(
t
)
y″ (t)+5y' (t)+6y(t)=4f' (t)+7f(t)
y″(t)+5y′(t)+6y(t)=4f′(t)+7f(t) ,试分别绘出在下列给定初始
(
1
)
y
(
0
−
)
=
1
,
y
′
(
0
−
)
=
−
1
(1) y(0_-)=1 ,y' (0_-)=-1
(1)y(0−)=1 ,y′(0−)=−1
(
2
)
y
(
0
−
)
=
2
,
y
′
(
0
−
)
=
1
(2) y(0_-)=2 ,y' (0_-)=1
(2)y(0−)=2 ,y′(0−)=1
第二部分:连续系统时域响应Multisim电路仿真分析
1. 在Multisim软件平台上,参照图7搭建仿真电路并连接相关仪器设备,设置好仪器的参数。
2. 二阶系统欠阻尼条件下的阶跃响应和冲激响应测试分析:
(1)根据(10)式,取R= (R取值在某个范围之内,请任意选择取值范围内的某个阻值,下同),系统将工作于欠阻尼模态;
(2)设置适当的激励信号,运行仿真电路,分别测试系统的阶跃响应、冲激响应,并记录保存实验结果波形(含激励和响应波形)。
3. 二阶系统临界阻尼条件下的阶跃响应和冲激响应测试分析:
(1)根据(10)式,取R= , 系统将工作于临界阻尼模态;
(2)参照欠阻尼条件下的测试步骤,完成系统单位阶跃响应与单位冲激响应的测试和记录。
4. 二阶系统过阻尼条件下的阶跃响应和冲激响应测试分析:
(1)根据(10)式,取R= ,系统将工作于过阻尼模态;
(2)参照欠阻尼条件下的测试步骤,完成系统单位阶跃响应与单位冲激响应的测试和记录。
5. 二阶不稳定系统时域响应的测试分析
(1)根据(10)式,取R= ,系统将不稳定;
(2)激励信号任意设置(或者设为0),运行仿真电路,观察并记录系统响应的变化情况。
6. 零输入响应的测试分析
(1)选择适当的外接电阻R,使系统工作于任意一种稳定状态(过阻尼、临界阻尼或欠阻尼);
(2)零输入响应测试:激励信号采用占空比50%的低频方波(注意使其低电平为0,即XFG2的偏置和幅度设置为相等的值)。运行电路,用方波的高电平作为初始状态激励输入,以方波的下降沿作为t=0时刻,开始记录零输入响应。
五、实验数据及结果分析
第一部分:连续系统时域响应MATLAB仿真分析
程序设计实验的程序及其结果分析
- 已知连续LTI系统,激励 f ( t ) = s i n ( 5 π t ) ε ( t ) f(t)=sin( 5πt)ε(t) f(t)=sin(5πt)ε(t),单位冲激响应 h ( t ) = 2 t e − 4 t ε ( t ) h(t)=2te^{-4t} ε(t) h(t)=2te−4tε(t) ,试绘出系统零状态响应 的波形。
>> p=0.01;
t=0:p:4
f1=sin(5*pi*t);
f2=2*t.*exp(-4*t);
lxjuanji (f1,f2,t,t,p);
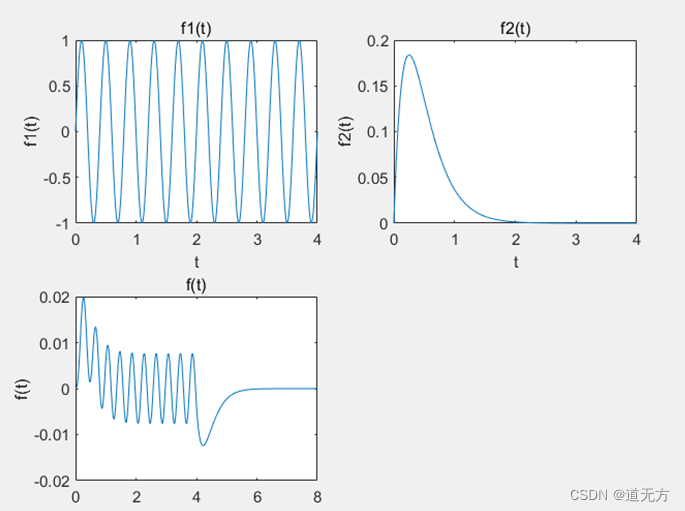
分析:MATLAB中卷积函数中只能求有限范围函数的卷积。本题中画出系统零状态响应 y z s ( t ) y_{zs} (t) yzs(t)的波形时,h(t)和f(t)中t的区间为(0,4),会导致零状态响应 y z s ( t ) y_{zs} (t) yzs(t)的波形只有一半(0,4)是准确的。后来我又扩大了h(t)和f(t)中t的区间范围,我观察发现 y z s ( t ) y_{zs} (t) yzs(t)的波形图中在t>2之后的均是按照余弦波的形式在0的上下震荡。
- 已知LTI系统,激励 f ( t ) = 3 t ε ( t ) f(t)=3tε(t) f(t)=3tε(t),单位冲激响应 h ( t ) = t e − 2 t ε ( t ) h(t)=te^{-2t} ε(t) h(t)=te−2tε(t) ,试给出系统零状态响应 y z s ( t ) y_{zs} (t) yzs(t)的数学表达式。
>> syms x;
t=sym('T','positive');
f=3*t;
h=t*exp(-2*t);
fh_x=subs(f,t,x)*subs(h,t,t-x);
yzs=int(fh_x,x,0,t)
yzs =
(3*T)/4 + (3*exp(-2*T))/4 + (3*T*exp(-2*T))/4 - 3/4
分析:该题的零状态响应等于激励与冲激响应的卷积,然后利用卷积的定义可以得到零状态响应。
- 试分别绘出下列微分方程描述的LTI系统单位冲激响应和阶跃响应的波形,并求出相应的数值解。
(1) 2 y ″ ( t ) + y ′ ( t ) + 8 y ( t ) = f ( t ) 2y″ (t)+y' (t)+8y(t)=f(t) 2y″(t)+y′(t)+8y(t)=f(t)
>> a=[2,1,8];
b=[1];
impulse(b,a,'R')
y1=impulse(b,a,0:2)
hold on
step(b,a,'k')
y2=step(b,a,0:2)
legend('冲激响应波形','阶跃响应波形')
y1 =
0
0.1797
-0.1125
y2 =
0
0.1529
0.1834
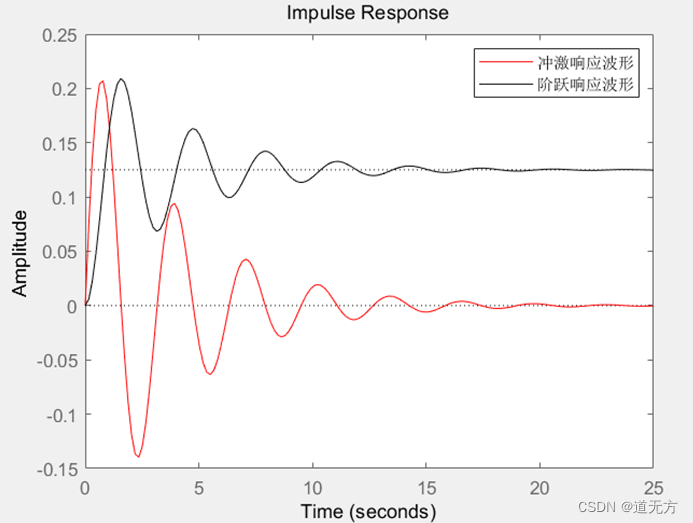
(2) 3 y ‴ ( t ) + 2 y ′ ( t ) − 4 y ( t ) = 2 f ′ ( t ) + f ( t ) 3y‴ (t)+2y' (t)-4y(t)=2f' (t)+f(t) 3y‴(t)+2y′(t)−4y(t)=2f′(t)+f(t)
>> a=[3,0,2,-4];b=[2,1];
impulse(b,a,'R')
y1=impulse(b,a,0:2)
hold on,step(b,a,'k')
y2=step(b,a,0:2)
legend('冲激响应波形','阶跃响应波形')
y1 =
0
0.7919
1.9756
y2 =
0
0.3768
1.7032
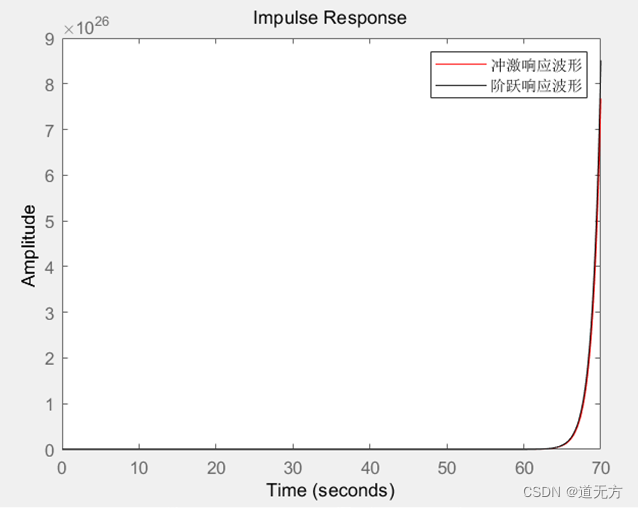
(3) y ″ ( t ) + 2 y ′ ( t ) + 5 y ( t ) = 4 f ′ ( t ) y″ (t)+2y' (t)+5y(t)=4f' (t) y″(t)+2y′(t)+5y(t)=4f′(t)
>> a=[1,2,5];
b=[4,0];
impulse(b,a,'R')
y1=impulse(b,a,0:2)
hold on
step(b,a,'k')
y2=step(b,a,0:2)
legend('冲激响应波形','阶跃响应波形')
y1 =
4.0000
-1.2814
-0.1490
y2 =
0
0.6690
-0.2048
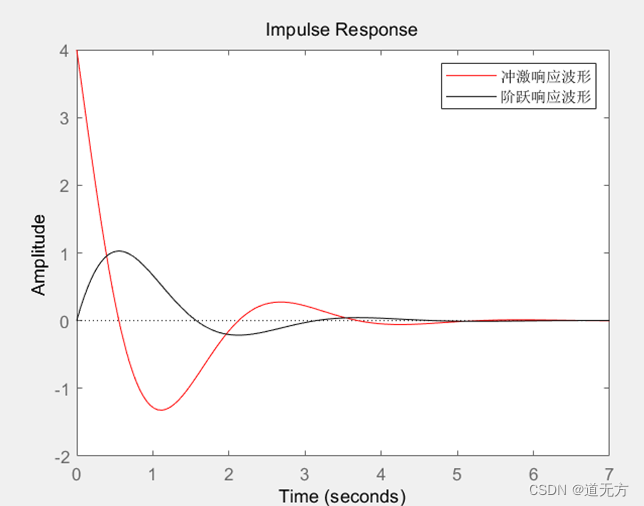
- 已知连续LTI系统,微分方程为
3
y
‴
(
t
)
+
5
y
″
(
t
)
+
7
y
′
(
t
)
+
y
(
t
)
=
f
′
(
t
)
+
f
(
t
)
3y‴ (t)+5y″ (t)+7y' (t)+y(t)=f' (t)+f(t)
3y‴(t)+5y″(t)+7y′(t)+y(t)=f′(t)+f(t) ,试分别绘出在下列给定初始条件下,系统零输入响应的波形。
(1) y ( 0 − ) = 2 , y ′ ( 0 − ) = 1 , y ″ ( 0 − ) = 0 y(0_-)=2 ,y' (0_-)=1 ,y″ (0_-)=0 y(0−)=2 ,y′(0−)=1 ,y″(0−)=0
>> a=[3,5,7,1];
y0=[0,1,2];
n=length(a)-1;
p=Roots(a);
V=Rot90(vandeR(p));
C=V\y0';
t=0.01;
t1=10;
t=0:t:t1;
yx=zeRos(1,length(t));
foR k=1:n;
yx=yx+C(k)*exp(p(k)*t);
end
plot(t,yx)
title('yx(t)')
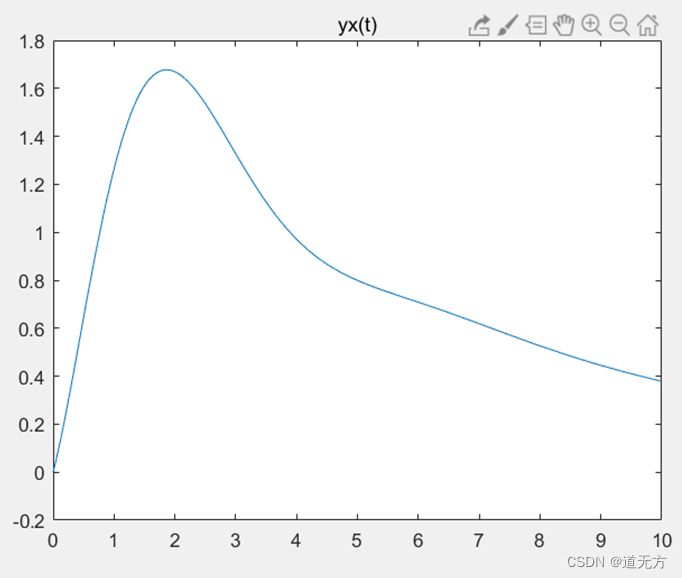
(2) y ( 0 − ) = 1 , y ′ ( 0 − ) = 0 , y ″ ( 0 − ) = 1 y(0_-)=1 ,y' (0_-)=0 ,y″ (0_-)=1 y(0−)=1 ,y′(0−)=0 ,y″(0−)=1
>> a=[3,5,7,1];
y0=[1,0,1];
n=length(a)-1;
p=Roots(a);
V=Rot90(vandeR(p));
C=V\y0';
t=0.01;
t1=10;
t=0:t:t1;
yx=zeRos(1,length(t));
foR k=1:n;
yx=yx+C(k)*exp(p(k)*t);
end
plot(t,yx),title('yx(t)')
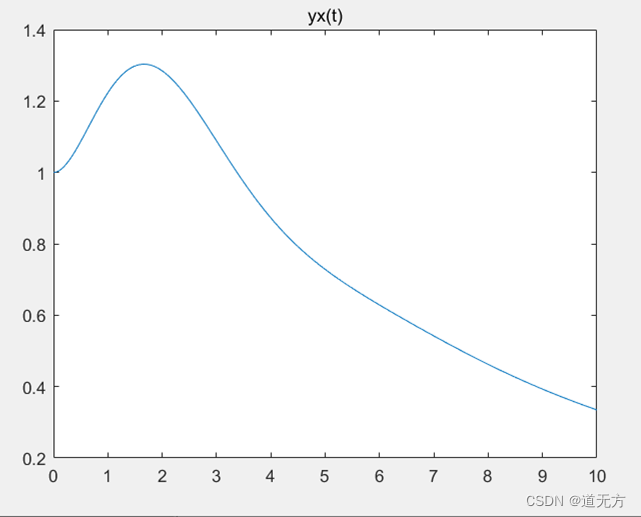
- 已知连续LTI系统,微分方程为
y
″
(
t
)
+
5
y
′
(
t
)
+
6
y
(
t
)
=
4
f
′
(
t
)
+
7
f
(
t
)
y″ (t)+5y' (t)+6y(t)=4f' (t)+7f(t)
y″(t)+5y′(t)+6y(t)=4f′(t)+7f(t) ,试分别绘出在下列给定初始条件下,系统零输入响应的波形。
(1) y ( 0 − ) = 1 , y ′ ( 0 − ) = − 1 y(0_-)=1 ,y' (0_-)=-1 y(0−)=1 ,y′(0−)=−1
>> a=[1,5,6];
y0=[-1,1];
n=length(a)-1;
p=Roots(a);
V=Rot90(vandeR(p));
C=V\y0';
t=0.01;
t1=10;
t=0:t:t1;
yx=zeRos(1,length(t));
foR k=1:n;
yx=yx+C(k)*exp(p(k)*t);
end
plot(t,yx)
title('yx(t)')
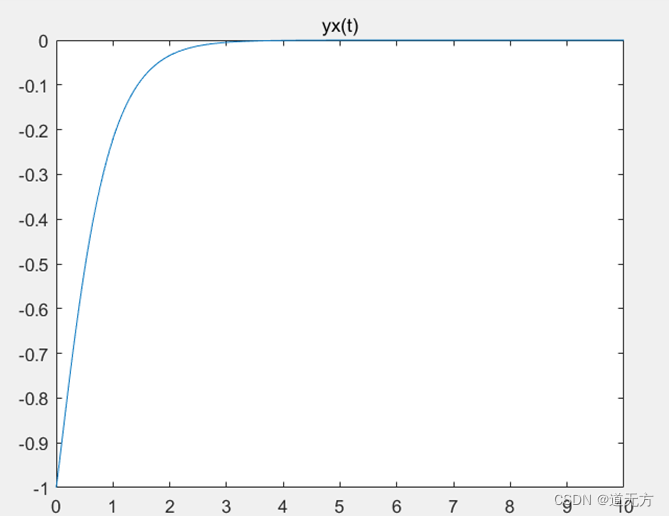
(2) y ( 0 − ) = 2 , y ′ ( 0 − ) = 1 y(0_-)=2 ,y' (0_-)=1 y(0−)=2 ,y′(0−)=1
>> a=[1,5,6];
y0=[1,2];
n=length(a)-1;
p=Roots(a);
V=Rot90(vandeR(p));
C=V\y0';
t=0.01;
t1=10;
t=0:t:t1;
yx=zeRos(1,length(t));
foR k=1:n;
yx=yx+C(k)*exp(p(k)*t);
end
plot(t,yx)
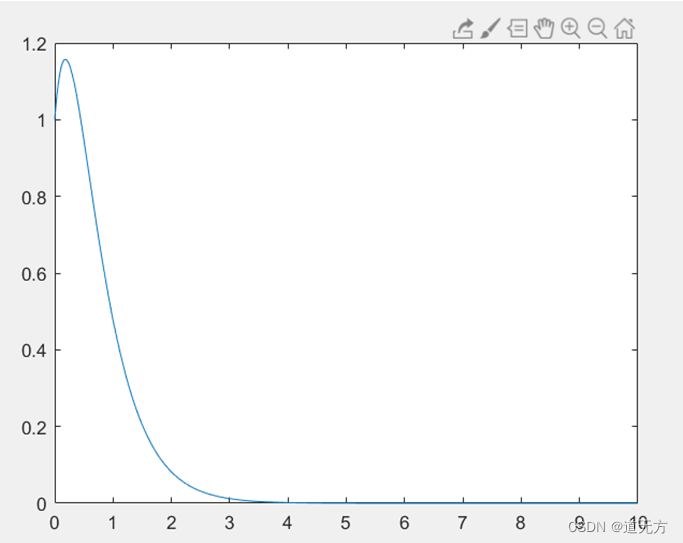
第二部分:连续系统时域响应Multisim电路仿真分析
1. 根据(10)式所描述的系统微分方程以及实验中各步骤选取的电阻R,采用软件进行仿真,求出各种情况下的微分方程特征根,分别画出系统在不同阻尼条件下的阶跃响应与冲激响应(利用阶跃响应函数step和冲激响应函数impulse),并与Multisim仿真结果进行比较,分析其差异的大小以及差异产生的原因。
解:将R1,R2,C1,C2的值带入微分方程得到
y
″
(
t
)
+
3
−
7.5
/
R
0.33
y
(
t
)
+
1
0.05445
y
(
t
)
=
1
+
7.5
/
R
0.05445
f
(
t
)
y^″ (t)+\frac{3-7.5/R}{0.33}y(t)+\frac{1}{0.05445}y(t)=\frac{1+7.5/R}{0.05445}f(t)
y″(t)+0.333−7.5/Ry(t)+0.054451y(t)=0.054451+7.5/Rf(t)
对比
y
″
(
t
)
+
2
ξ
ω
n
y
′
(
t
)
+
ω
n
2
y
(
t
)
=
K
ω
n
2
f
(
t
)
y″ (t)+2ξω_n y' (t)+ω_n^2 y(t)=Kω_n^2 f(t)
y″(t)+2ξωny′(t)+ωn2y(t)=Kωn2f(t) 可得:
ω
n
=
4.285
,
ξ
=
3
−
7.5
/
R
2.828
ω_n=4.285,ξ=\frac{3-7.5/R}{2.828}
ωn=4.285,ξ=2.8283−7.5/R
1.无阻尼
A、情景一:无阻尼(ξ=0),解得R=2.5k。此时取R=2.5k,微分方程为
y
″
(
t
)
+
y″ (t)+
y″(t)+
1
0.05445
\frac{1}{0.05445}
0.054451
y
(
t
)
=
y(t)=
y(t)=
4
0.05445
\frac{4}{0.05445}
0.054454
f
(
t
)
f(t)
f(t),特征根为一对纯虚根
s
1
,
2
=
−
ξ
ω
n
±
ω
n
(
ξ
2
−
1
)
1
/
2
=
±
j
ω
n
=
±
4.285
j
s_{1,2}=-ξω_n±ω_n (ξ^2-1)^{1/2}=±jω_n=±4.285j
s1,2=−ξωn±ωn(ξ2−1)1/2=±jωn=±4.285j 。
1.MATLAB仿真:
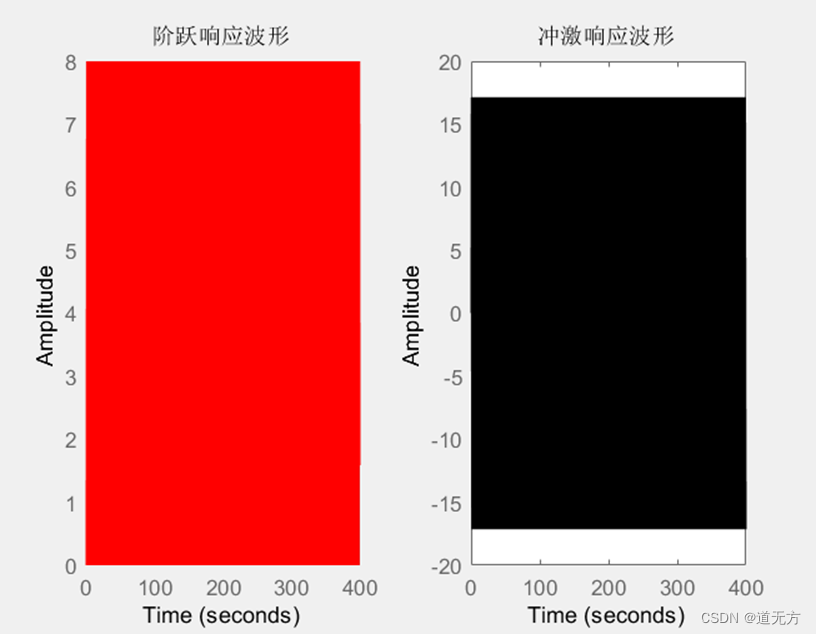
2. Multisim仿真
(1)阶跃响应波形(频率:0.1Hz,占空比:99%,振幅:50Vp,偏置:50V下面的阶跃响应参数同下)
(2)冲激响应波形(频率:0.1Hz,占空比:1%,振幅:10Vp,偏置:10V下面的阶跃响应参数同下)
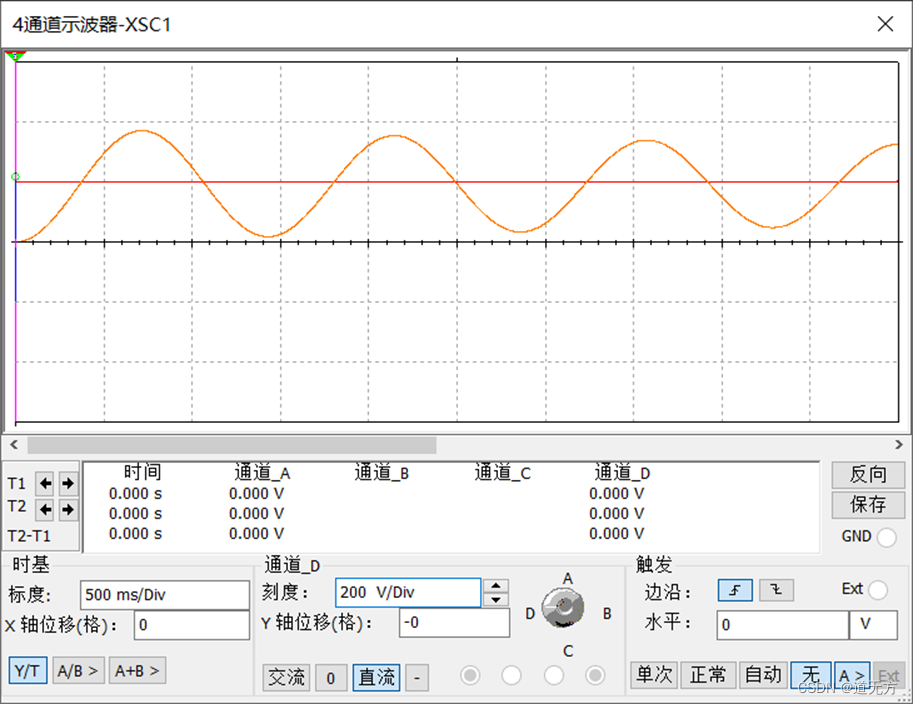
分析:MATLAB仿真的阶跃和冲激响应均是全图充满,而Multisim仿真的均是上下震荡(理论上应该是等幅振荡)。差异可能原因:无阻尼下,阶跃响应函数step和冲激响应函数impulse的图形十分紧凑,可以看成是Multisim仿真中x轴标度无穷大(已经试验过了),产生的图案与MATLAB类似。
2.欠阻尼
B、情景二:欠阻尼
(
0
<
ξ
<
1
)
(0<ξ<1)
(0<ξ<1),解得
2.5
k
<
R
<
43.604
k
2.5k<R<43.604k
2.5k<R<43.604k。此时取
R
=
6
k
R=6k
R=6k,微分方程为
y
″
(
t
)
+
175
/
33
y
(
t
)
+
1
/
0.05445
y
(
t
)
=
2.25
/
0.05445
f
(
t
)
y″ (t)+175/33 y(t)+1/0.05445 y(t)=2.25/0.05445 f(t)
y″(t)+175/33y(t)+1/0.05445y(t)=2.25/0.05445f(t),特征根为一对不等的共轭负根
s
1
,
2
=
−
ξ
ω
n
±
ω
n
(
ξ
2
−
1
)
1
/
2
=
−
ξ
ω
n
±
j
ω
n
(
1
−
ξ
2
)
1
/
2
=
−
2.652
±
3.366
j
s_{1,2}=-ξω_n±ω_n (ξ^2-1)^{1/2}=-ξω_n±jω_n (1-ξ^2 )^{1/2}=-2.652±3.366j
s1,2=−ξωn±ωn(ξ2−1)1/2=−ξωn±jωn(1−ξ2)1/2=−2.652±3.366j。
MATLAB仿真:
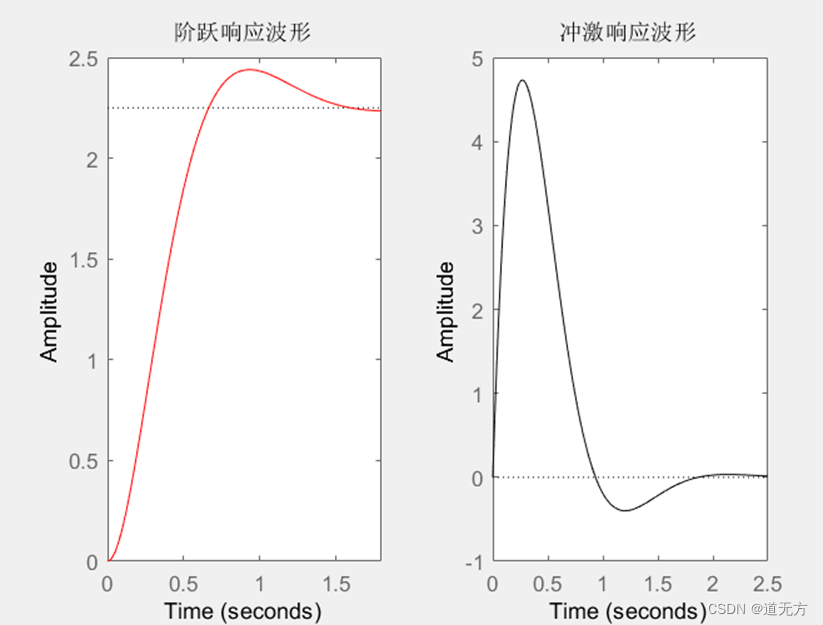
2. Multisim仿真
(1)阶跃响应波形
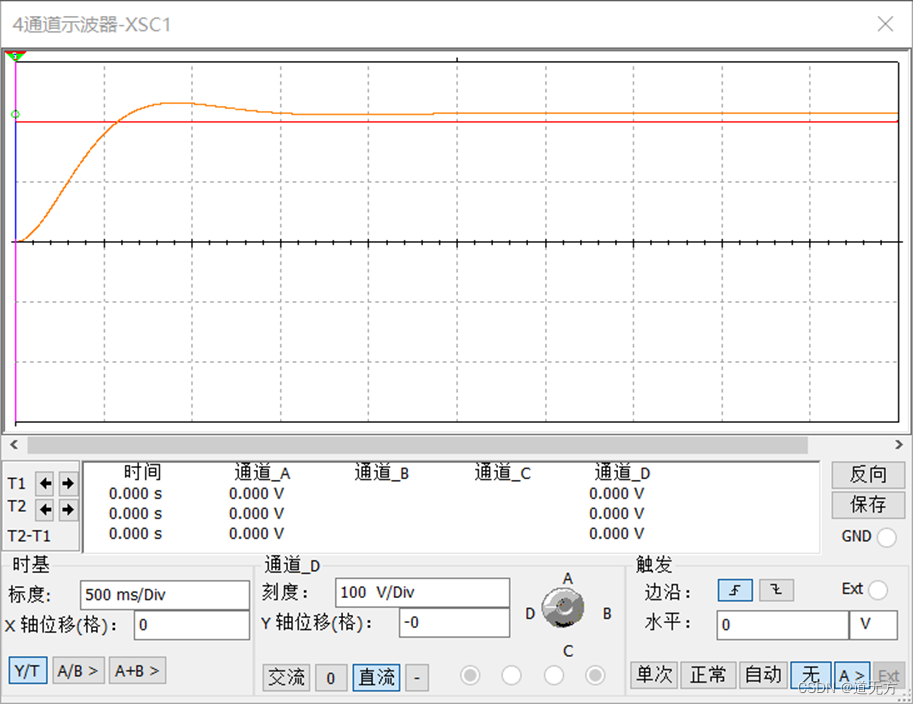
(2)冲激响应波形
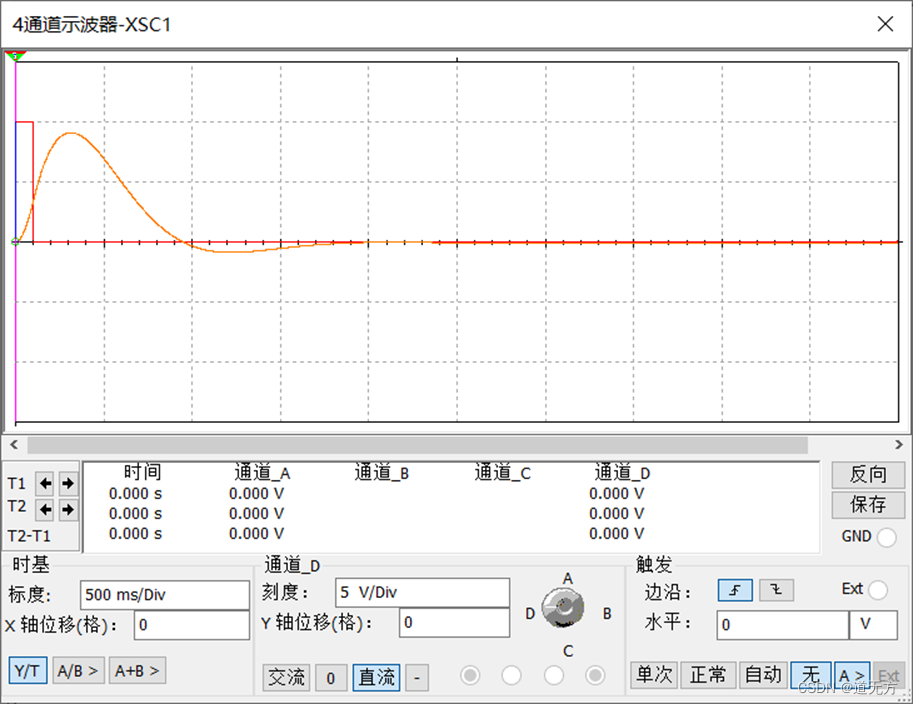
分析:MATLAB和Multisim分别对应的阶跃响应和冲激响应波形类似。
3.临界阻尼
C、临界阻尼
(
ξ
=
1
)
(ξ=1)
(ξ=1),解得
R
=
43.604
k
R=43.604k
R=43.604k。此时取
R
=
43.604
k
R=43.604k
R=43.604k,微分方程为
y
″
(
t
)
+
8.57
y
(
t
)
+
1
/
0.05445
y
(
t
)
=
21.524
f
(
t
)
y″ (t)+8.57y(t)+1/0.05445 y(t)=21.524f(t)
y″(t)+8.57y(t)+1/0.05445y(t)=21.524f(t),特征根为一对相等的负实根
s
1
,
2
=
−
ξ
ω
n
±
ω
n
(
ξ
2
−
1
)
1
/
2
=
−
ξ
ω
n
=
−
4.285
s_{1,2}=-ξω_n±ω_n (ξ^2-1)^{1/2}=-ξω_n=-4.285
s1,2=−ξωn±ωn(ξ2−1)1/2=−ξωn=−4.285。
1.MATLAB仿真:

- Multisim仿真
(1)阶跃响应波形
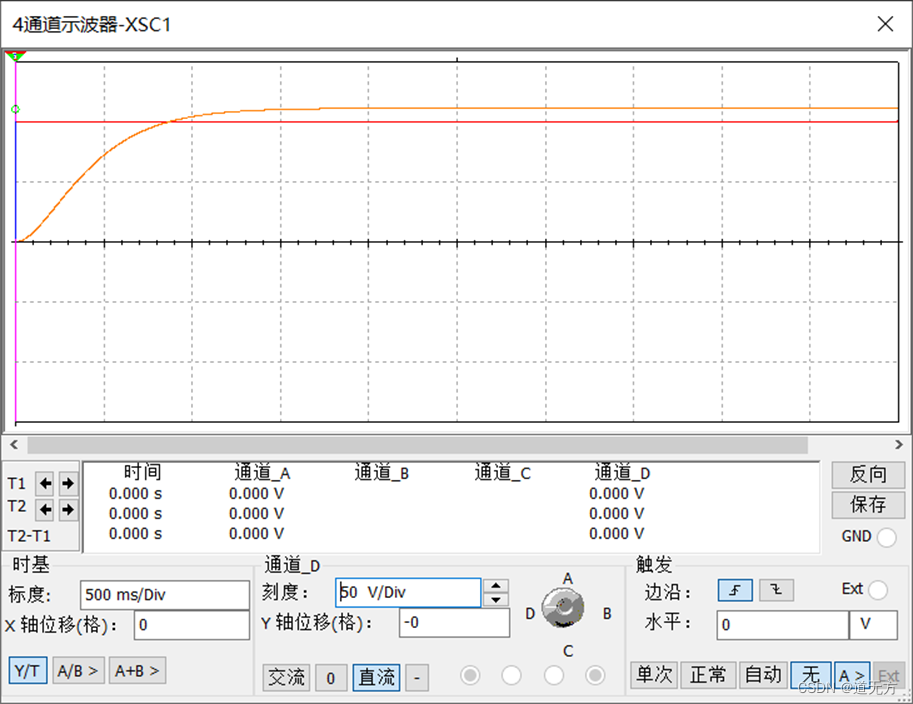
(2)冲激响应波形
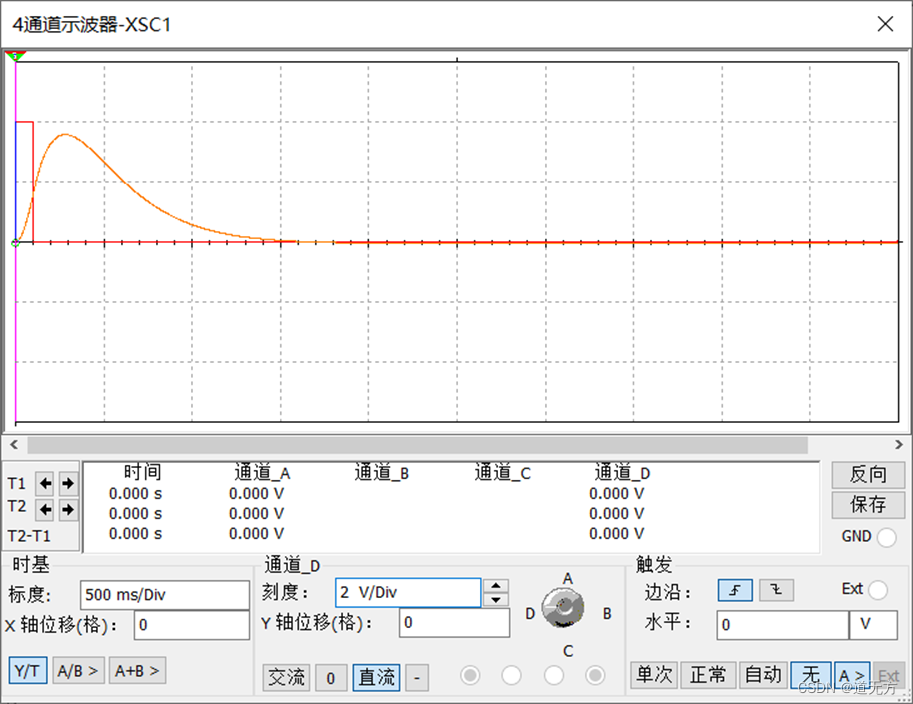
分析:MATLAB和Multisim分别对应的阶跃响应和冲激响应波形类似。
4.过阻尼
D、过阻尼
(
ξ
>
1
)
(ξ>1)
(ξ>1),解得
R
>
43.604
k
R>43.604k
R>43.604k。此时取
R
=
100
k
R=100k
R=100k,微分方程为
y
″
(
t
)
+
2.295
/
0.33
y
(
t
)
+
1
/
0.05445
y
(
t
)
=
1.075
/
0.05445
f
(
t
)
y″ (t)+2.295/0.33 y(t)+1/0.05445 y(t)=1.075/0.05445 f(t)
y″(t)+2.295/0.33y(t)+1/0.05445y(t)=1.075/0.05445f(t),特征根为一对不等的负实根
s
1
,
2
=
−
ξ
ω
n
±
ω
n
(
ξ
2
−
1
)
1
/
2
=
−
3.304
或
−
5.558
s_{1,2}=-ξω_n±ω_n (ξ^2-1)^{1/2}=-3.304或-5.558
s1,2=−ξωn±ωn(ξ2−1)1/2=−3.304或−5.558。
1.MATLAB仿真:
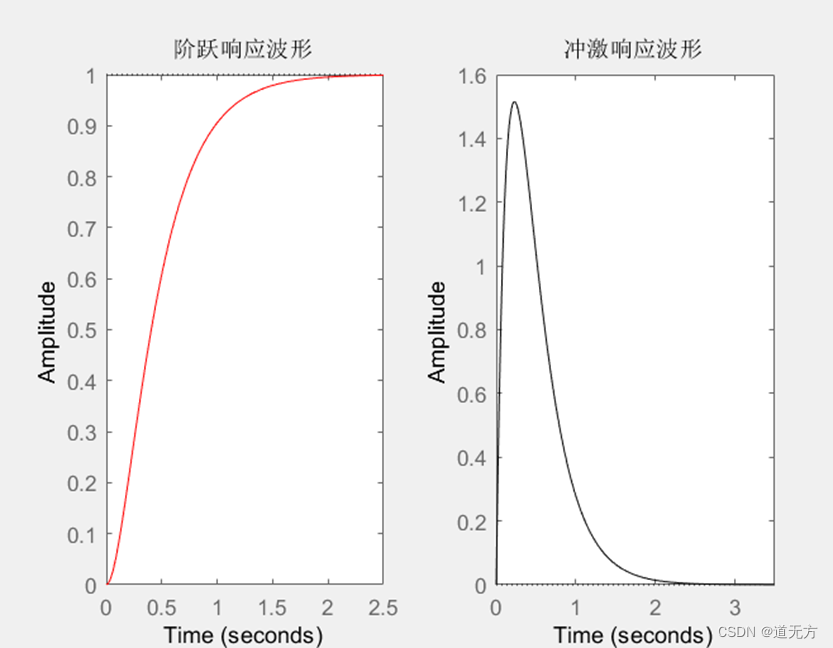
2. Multisim仿真
(1)阶跃响应波形
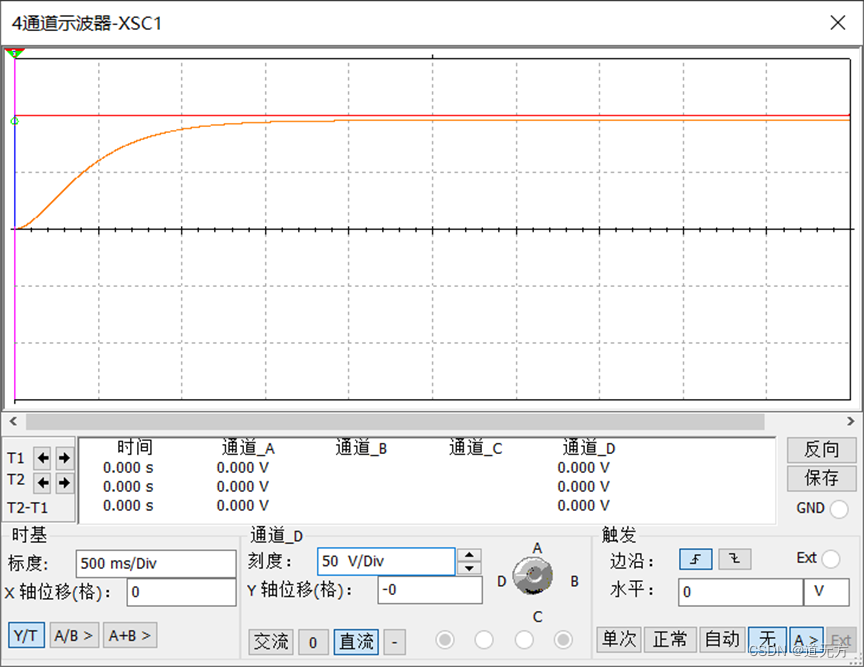
(2)冲激响应波形
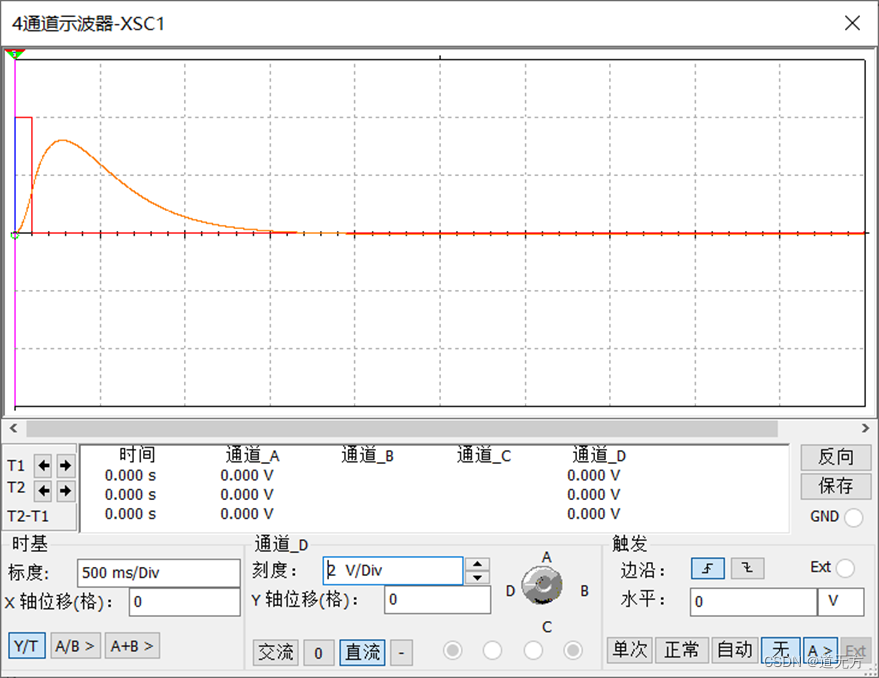
分析:MATLAB和Multisim分别对应的阶跃响应和冲激响应波形类似。
5.二阶不稳定系统
E、二阶不稳定系统 ( ξ < 0 ) (ξ<0) (ξ<0),解得 0 < R < 2.5 k 0<R<2.5k 0<R<2.5k。此时取 R = 1 k R=1k R=1k,微分方程为 y ″ ( t ) + ( − 4.5 ) / 0.33 y ( t ) + 1 / 0.05445 y ( t ) = 8.5 / 0.05445 f ( t ) y″ (t)+(-4.5)/0.33 y(t)+1/0.05445 y(t)=8.5/0.05445 f(t) y″(t)+(−4.5)/0.33y(t)+1/0.05445y(t)=8.5/0.05445f(t),特征根的实部为正, s 1 , 2 = − ξ ω n ± ω n ( ξ 2 − 1 ) 1 / 2 = − 1.514 或 − 12.122 s_{1,2}=-ξω_n±ω_n (ξ^2-1)^{1/2}=-1.514或-12.122 s1,2=−ξωn±ωn(ξ2−1)1/2=−1.514或−12.122。
1.MATLAB仿真: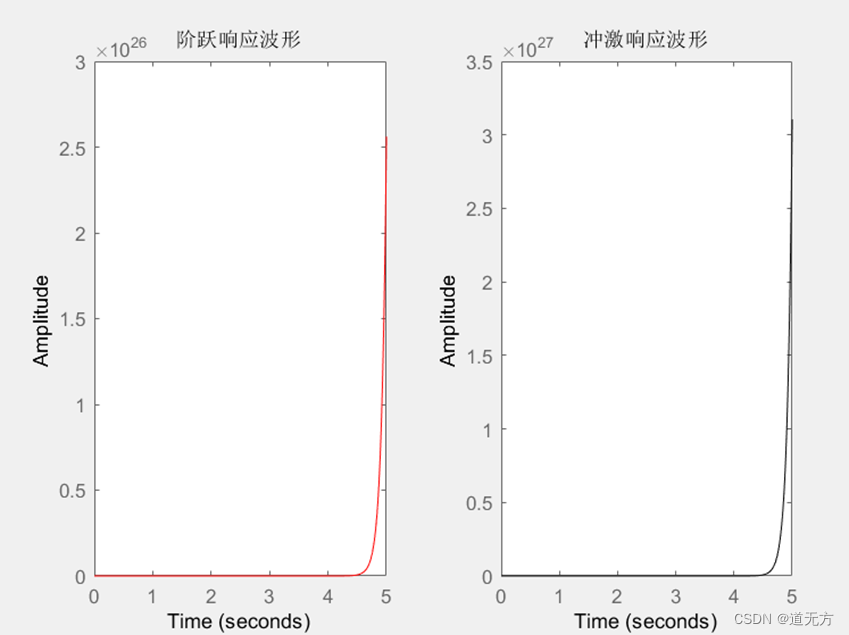
2. Multisim仿真
(1)阶跃响应波形
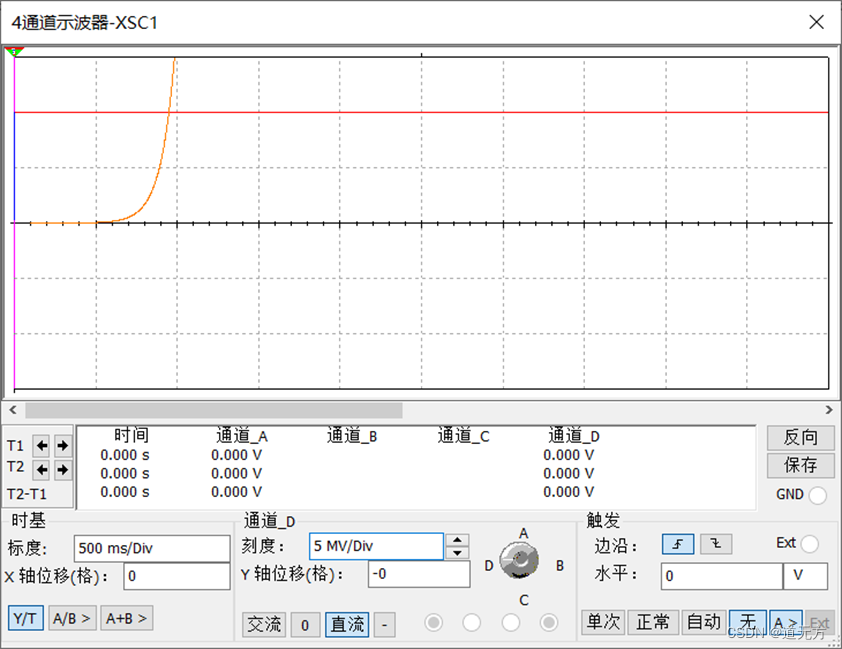
(2)冲激响应波形
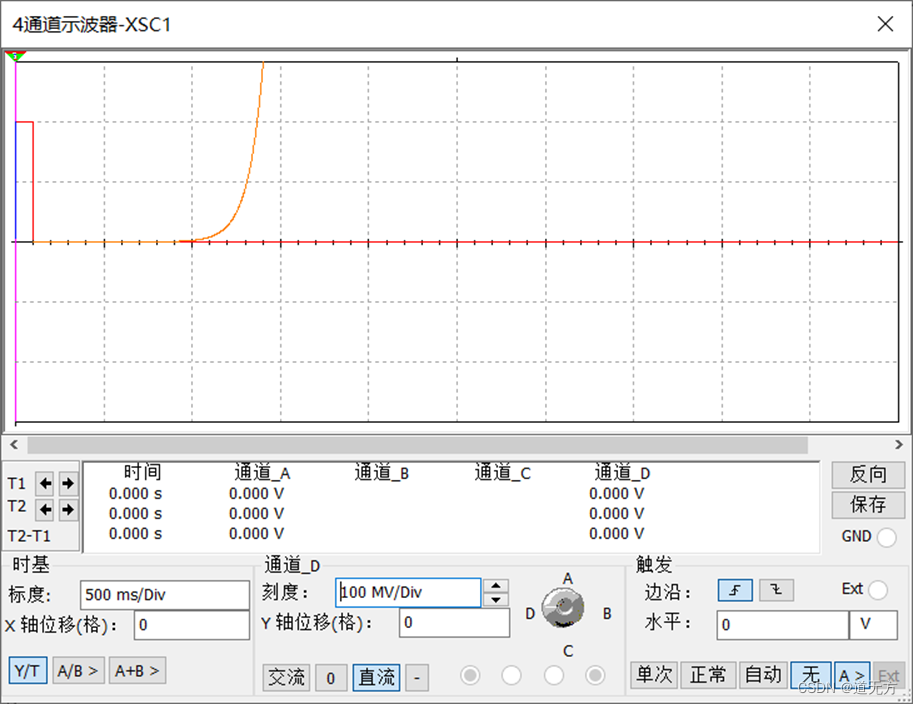
分析:MATLAB和Multisim分别对应的阶跃响应和冲激响应波形类似。
2. 比较不同阻尼条件下时域响应(包括阶跃响应与冲激响应)的区别,据此分析系统参数以及微分方程特征根对系统固有响应的影响。
答:不同阻尼条件下阶跃响应与冲激响应的时域响应的波形是不一样的。通过对上述波形的分析,可以得到:
当 ξ=0时,二阶系统为无阻尼状态,阶跃,冲激响应均为等幅上下震荡。
当 0<ξ<1时,二阶系统为欠阻尼状态,阶跃,冲激响应均为幅度不断衰减的上下震荡,然后趋于0或1。不同的是冲激响应趋于0,而阶跃响应趋于1。
当 ξ=1时,二阶系统为临界阻尼状态,阶跃响应开始迅速增大,然后增速减缓,趋于1。而冲激响应开始迅速增大,然后开始下降,趋于0
当 ξ>1时,二阶系统为过阻尼状态,阶跃,冲激响应的波形与ξ=1的波形近似,不同的是阶跃,冲激响应开始迅速增大的程度减缓。
当 ξ<0时,系统不稳定,阶跃,冲激响应均在某一个时间迅猛增大。
六、实验结论
1.LTI零状态响应等于激励信号与冲激响应的卷积。
2.MATLAB专门为用户提供了求连续时间系统单位冲激响应及单位阶跃响应,并绘制其时域波形的函数impulse()和 step()。
3. ξ不同,二阶系统对应着不同的状态。其具体情况在上面已有概述。
七、思考题
第一部分:连续系统时域响应MATLAB仿真分析
1.求两个定义域(0,∞)的函数卷积的波形时,利用M脚本(卷积函数的算法)求得的波形图是不对的,该如何改正?
答:以程序设计实验的第一个为例(和老师上课讲的验证性试验的题型是一致的),具体的分析已经在前面提到了,对信号采取截断处理尽管存在误差,但是通过选择合理的信号长度,这种误差是能够减小到可以接受的程度的。
第二部分:连续系统时域响应Multisim电路仿真分析
1.Multisim电路仿真上课老师没有留思考题。但是试验报告的第五部分我只进行了零状态响应,所以我在这进行零输入响应的测试分析
答:(1)选择适当的外接电阻R=6k,使系统工作于任意一种稳定状态—欠阻尼;
(2)零输入响应测试:激励信号采用占空比50%的低频方波(注意使其低电平为0,即XFG2的偏置和幅度设置为相等的值)。运行电路,用方波的高电平作为初始状态激励输入,以方波的下降沿作为t=0时刻,开始记录零输入响应。
Multisim仿真(频率:0.1Hz,占空比:1%,振幅:10Vp,偏置:10V)
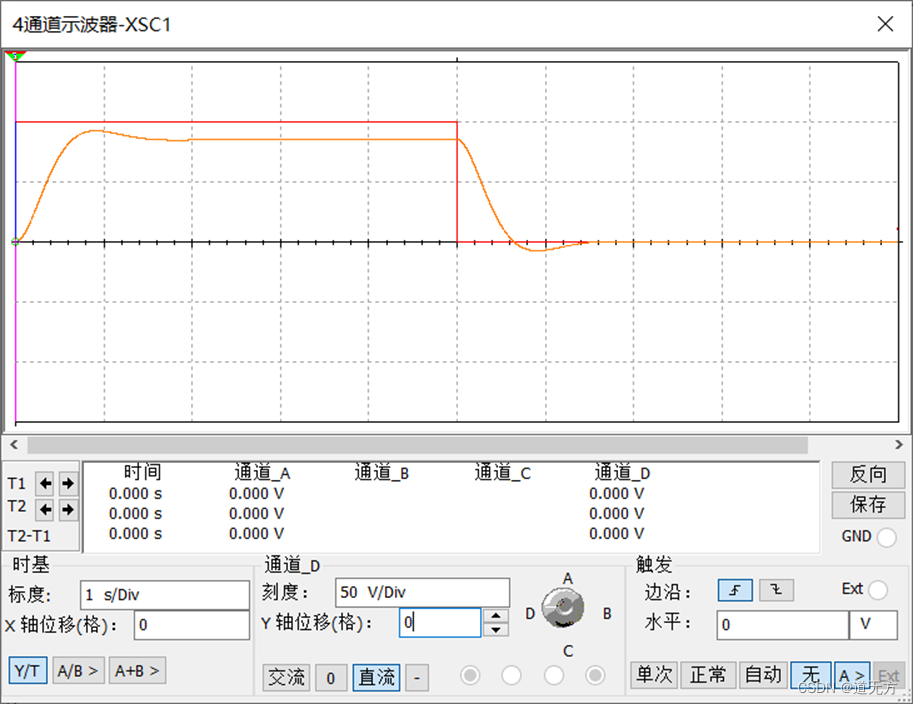
八、其他
通过本次实验,我了解到了LTI连续时间系统的时域分析方法,熟悉系统的零输入响应、零状态响应及冲激响应的求解步骤;并能利用MATLAB和Multisim求连续系统的冲激响应h(t)、阶跃响应、求连续系统对任意激励的零状态响应;并且通过图形可以看出ξ对冲激响应和阶跃响应的影响。