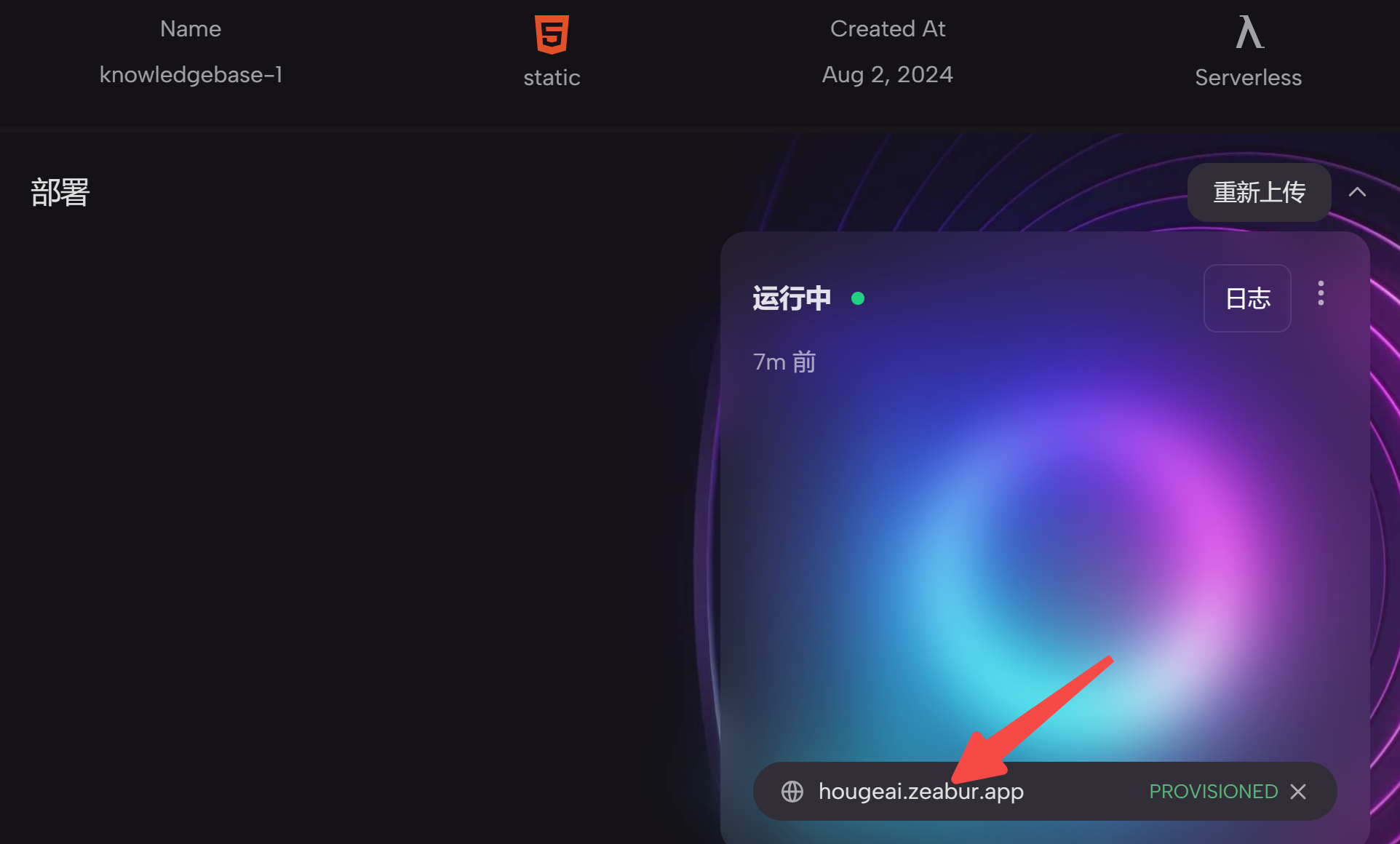
在如今激烈的超竞争时代，企业面临着巨大的挑战与机遇。要想在这个充满变革与风险的时代中立于不败之地，关键在于如何创新突破，借力于先进科技和智能系统，实现商业的辉煌。而"企元数智"作为您的得力助手，借力于欧赛斯先进科技，将助您在市场中脱颖而出，实现商业的巅峰。

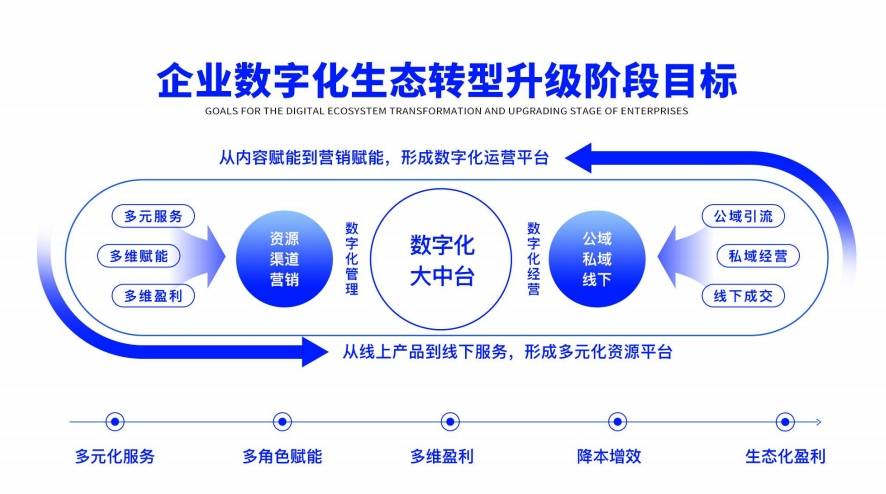
开启智能化商业新征程

"企元数智"与欧赛斯的强强合作，将开启智能化商业新征程。通过充分利用欧赛斯的领先科技，"企元数智"将为您提供一体化的智能解决方案，助您把握商机，优化运营效率，开拓市场，实现商业的持续辉煌。

提升品牌影响力，跻身市场领先者

借助"企元数智"携手欧赛斯的先进技术，您将能够快速提升品牌的影响力，在市场中脱颖而出。通过系统的智能营销和数据分析功能，您可以更好地了解市场需求，精准定位目标客户，实现品牌的快速传播，成为行业的领先者。

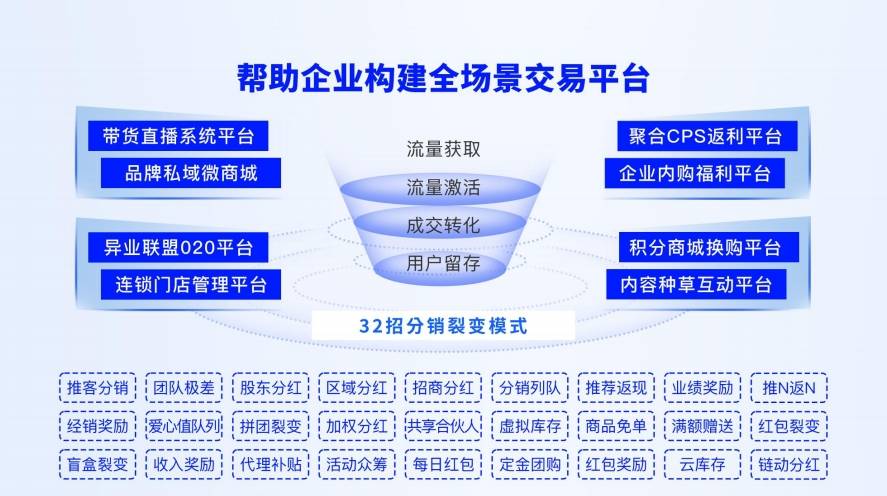
强化运营效能，实现商业繁荣

"企元数智"借助欧赛斯先进科技，将帮助您强化企业的运营效能，实现商业的繁荣。无论是销售管理、客户服务还是数据分析，系统将为您提供智能化的解决方案，帮助您优化业务流程，提升生产效率，从而实现商业的持续发展与繁荣。

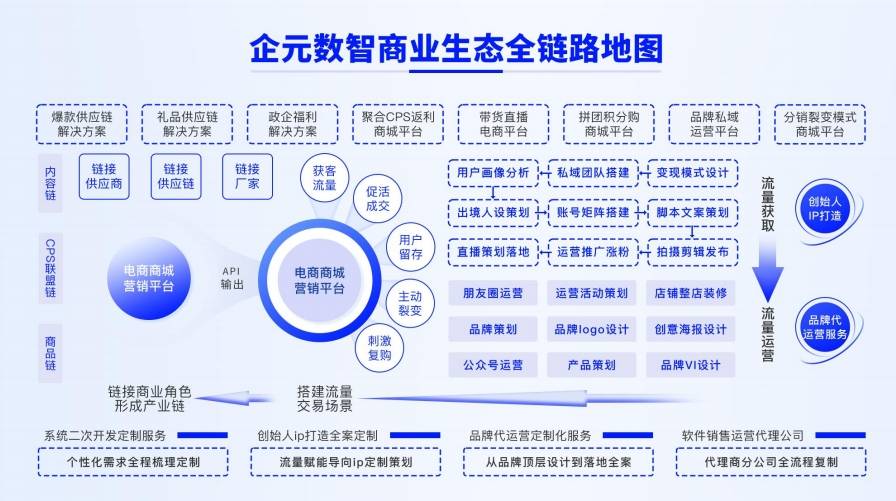
"企元数智"携手欧赛斯，助您突破超竞争时代，实现商业的辉煌。现在就行动起来，借力先进科技，抓住商机，开创企业的新未来！让我们携手同行，共创商业辉煌！