束搜索
为了量化解码器的计算代价,用 y y y表示输出词表,其中包含 < e o s > <eos> <eos>,词表大小则为 ∣ y ∣ |y| ∣y∣,指定输出序列的最大词元数为 T ′ T' T′,则我们的目标是从所有 O ( ∣ y ∣ T ′ ) O(|y|^{T'}) O(∣y∣T′)个可能得输出序列中寻找理想的输出。当然,对于所有输出序列,在 < e o s > <eos> <eos>之后的部分将在实际输出中丢弃
1. 贪心搜索
即输出最高条件概率的词元。

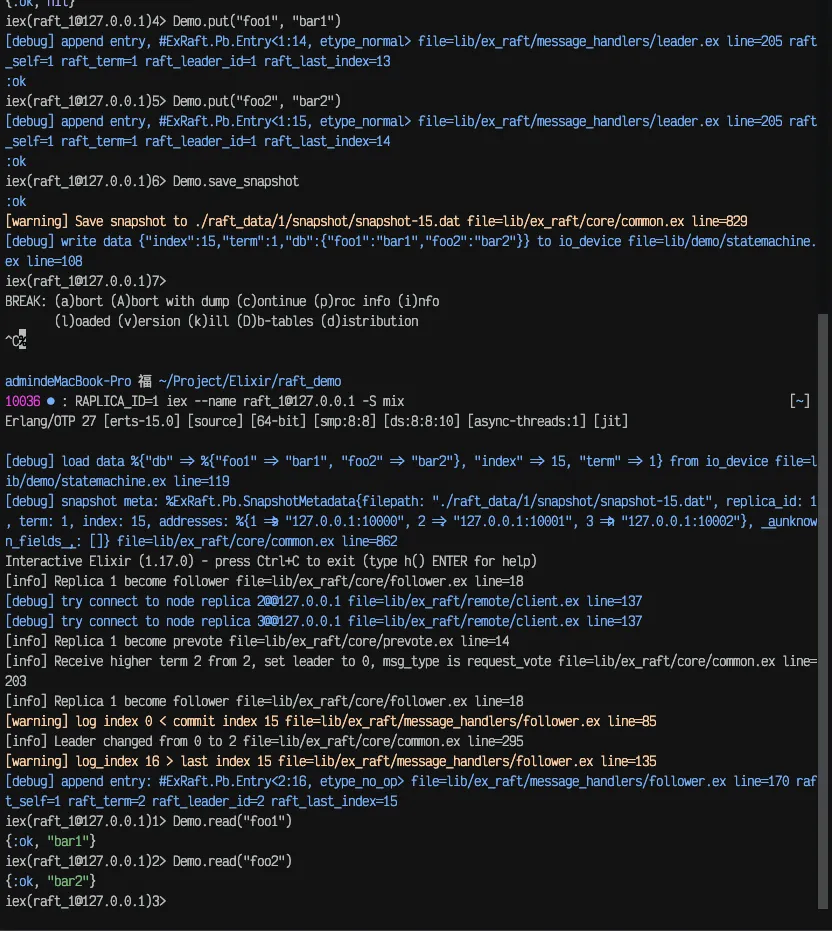
在每一个时间步,贪心搜索选择具有最高条件概率的词元,那么显然,如上图所示,输出序列"A B C <eos>"的条件概率最大。
但贪心搜索显然存在问题,局部最优的和不一定是全局最优,实际上,最优序列应该是最大化 Π t ′ = 1 T ′ P ( y t ′ ∣ y 1 , ⋯ , y t ′ − 1 , c ) \Pi^{T'}_{t'=1}P(y_{t'}|y_1,\cdots,y_{t'-1},c) Πt′=1T′P(yt′∣y1,⋯,yt′−1,c)值的输出序列,这是基于输入序列生成输出序列的条件概率。
例如,我们在第二时间步选择C,可能会发生一以下变化:

第三时间步的条件概率发生了变化,而0.5 * 0.3 *0.6 *0.6更大了。这不一定是最优序列,但的确比贪心搜索的局部最优好。
2.穷举搜索
字面意思,搜索所有的序列,这是不可能的,计算量太大了
3.束搜索
束搜索(beam search)是贪心搜索的一个改进版本,有一个超参数,名为束宽 k k k,在时间步1,我们选择具有最高条件概率的k个词元,并且每次都基于上一时间的k个候选输出序列,继续从 k ∣ y ∣ k|y| k∣y∣个可能中选择最高概率的k个候选输出序列。(类似k叉树)

k=2,输出序列的最大长度为3
时间复杂度 O ( k n T ) O(knT) O(knT)