物理动力系统的强化学习：一种替代方法

一、物理和非线性动力学

控制理论通过经典的、鲁棒的和最优的方法，使现代文明成为可能。炼油、电信、现代制造业等都依赖于它们。控制理论建立在物理方程提供的洞察力之上，例如从牛顿定律和麦克斯韦方程派生出来。这些方程描述了物理系统上的动力学，即不同力的相互作用。通过它们，我们了解了方程如何在状态之间移动，其中状态是“充分描述系统的所有信息的集合”[1]，通常以流体动力学中流体粒子的压力或速度等变量表示，或电动力学中的电荷和电流状态。通过推导系统的方程，我们可以预测状态如何随时间和空间变化，并用微分方程来表达这种演变。有了这种理解，我们就可以以特殊施加的力的形式应用控制，以将这些系统保持在所需的状态或输出。通常，该力是根据系统的输出计算得出的。考虑车辆巡航控制。输入是期望的速度，输出是实际速度。系统就是引擎。状态估计器观察速度并确定输出速度和输入速度之间的差异，以及如何应用控制（例如调整燃油流量）以减少误差。

然而，尽管取得了所有成就，但控制理论遇到了很大的局限性。大多数控制理论都是围绕线性系统构建的，或者说，输入的比例变化导致输出的比例变化的系统。虽然这些系统可能相当复杂，但我们对这些系统有广泛的了解，使我们能够实际控制从深海潜水器和采矿设备到航天器的一切。

然而，正如斯坦尼斯拉夫·乌拉姆（Stanislaw Ulam）所说，“使用像非线性科学这样的术语，就像将大部分动物学称为对非大象动物的研究。到目前为止，我们在控制复杂物理系统方面的进展主要是通过找到将它们限制为线性行为的方法来实现的。这可能会以多种方式降低我们的效率：

·将复杂系统分解为单独控制的组件，从而针对子系统而不是整个系统进行优化

·以更简单但效率较低的操作模式操作系统，或者不利用复杂的物理特性，例如主动流量控制来减少飞机阻力

·严格的运行条件限制，如果超过该限制，可能会导致不可预测或灾难性的故障

先进的制造、改进的空气动力学和复杂的电信都将受益于更好的非线性系统控制方法。

非线性动力系统的基本特征是它们对输入的复杂响应。即使环境或状态发生微小变化，非线性系统也会发生巨大变化。考虑控制流体流动的纳维-斯托克斯方程：同一组方程将平静、缓慢流动的流描述为汹涌的洪流，并且汹涌洪流的所有涡流和特征都包含在方程动力学中。

非线性系统存在困难：与线性系统不同，我们通常对系统从一种状态过渡到另一种状态时的行为方式没有一个易于预测的概念。我们能做的最好的方法是通过一般分析或广泛的模拟。因此，对于非线性系统，我们面临着两个问题：系统识别——即理解它在给定状态下的行为方式，以及系统控制——它如何在短期和长期内响应给定的输入而变化，以及进行什么输入以获得期望的结果。

二、物理强化学习

虽然非线性分析和控制继续取得进展，但我们使用传统的、基于方程的方法利用这些系统的能力仍然有限。然而，随着计算能力和传感器技术变得越来越容易获得，基于数据的方法提供了一种不同的方法。

数据可用性的大幅增加催生了机器学习（ML）方法，而强化学习（RL）提供了一种新方法，可以更有效地应对控制非线性动态系统的挑战。RL已经在从自动驾驶汽车到策略和计算机游戏的环境中取得了成功，它是一种ML框架，它训练算法或代理，“学习如何在不确定性下做出决策，通过反复试验来最大化长期利益”[1]。换言之，强化学习算法解决了系统识别和控制优化的问题，它不是通过操纵和分析控制方程来实现的，而是通过对环境进行采样来预测哪些输入动作会导致预期的结果。RL 算法或代理根据系统状态应用操作策略，并在分析系统上的更多信息时优化此策略。

许多 RL 算法都基于使用神经网络来开发将状态映射到最优行为的函数。RL 问题可以定义为状态-动作-奖励元组。对于给定的状态，某个动作会导致给定的奖励。神经网络充当通用函数逼近器，可以进行调整以准确近似整个系统中的状态-动作-奖励元组函数。为此，它必须通过探索系统或环境来获取新知识，然后通过利用获得的额外数据来完善其策略。RL 算法的区别在于它们如何应用数学来探索、利用两者之间的波段平衡。

然而，神经网络带来了一些挑战：

·所需资源。使用神经网络来估计一个函数，该函数可以确定每个状态的奖励和采取的最佳行动，这可能需要相当多的时间和数据。

·可解释性。通常很难理解神经网络是如何得出它们的解决方案的，这限制了它们提供真正洞察力的效用，并可能使预测或约束神经网络的动作变得困难。可解释性对于物理系统尤为重要，因为它允许使用几个世纪的数学中开发的强大分析工具来获得对系统的更多了解。

虽然有一些方法可以解决这些挑战，例如迁移学习和拓扑分析，但它们仍然是强化学习更全面应用的障碍。但是，在我们专门研究物理系统的情况下，另一种方法可能很有用。回想一下，我们正在讨论的物理系统是由数学方程定义的，或者可以用数学方程很好地描述。我们不必开发一个完全任意的函数，而是可以专注于尝试找到一个由常见的数学运算符组成的表达式：算术、代数和超越函数（sine、e^x 等）。或者意味着为此目的将使用遗传算法。如[2]所述，遗传算法可以通过随机生成函数来探索函数空间，并通过突变和杂交育育有前途的候选者来开发和提炼解决方案。

因此，虽然神经网络是大多数RL问题的拥护者，但对于物理动力学来说，一个新的挑战者出现了。接下来，我们将仔细研究通用算法方法，看看它如何与领先的 RL 算法、软演员评论家相抗衡。为此，我们将使用 AWW Sagemaker Experiments 在基于物理的体育馆中评估两者。最后，我们将评估结果，讨论结论，并提出下一步建议。

回想一下，RL面临着两个挑战，探索环境和利用发现的信息。考虑到处于任何状态的可能性，有必要进行探索以找到最佳政策。如果未能探索，则意味着可能会错过局部全局最优值，并且算法可能无法充分泛化以在所有状态下都取得成功。需要进行开发，以将当前解决方案优化到最佳状态。然而，当算法对特定解决方案进行优化时，它会牺牲进一步探索系统的能力。

Soft Actor Critic （SAC）是对强大的 Actor-Critic RL 方法的改进。Actor-Critic 算法系列通过将状态值和相关奖励的估计与优化特定的输入策略分开来处理探索/利用权衡。当算法收集新信息时，它会更新每个估计器。Actor-Critic 的实现有许多细微差别;有兴趣的读者应查阅书籍或在线教程。SAC通过支持对奖励与批评者估计的截然不同的国家的探索来优化批评者。OpenAI 提供了 SAC 的详细说明。

在这个实验中，我们使用 SAC 的 Coax 实现。我查看了几个 RL 库，包括 Coach 和 Spinning Up，但 Coax 是我发现在当前 Python 构建中大部分“开箱即用”的少数几个库之一。Coax 库包含各种 RL 算法，包括 PPO、TD3 和 DDPG，适用于体育馆。

Actor-critic 方法（如 SAC）通常通过神经网络作为函数逼近器来实现。正如我们上次所讨论的，还有另一种可能的方法来探索系统和利用潜在的控制策略。遗传算法通过随机生成可能的解决方案进行探索，并通过突变或组合不同解决方案的元素（育种）来利用有前途的策略。在这种情况下，我们将评估遗传算法的遗传编程变体作为函数逼近的替代手段;具体来说，我们将使用遗传方法随机生成并评估包含常数、状态变量和数学函数的函数树作为潜在的控制器。

实现的遗传编程（GP）算法改编自 [2]，除了该文本使用的 tournament 代替，此实现选择每代的前 64%（Nn 低于 33%）作为符合突变条件，并重新播种其余部分以更好地探索解决方案空间。为了在一代中创建每棵树，增长函数从算术函数（+,-,*， /）和超越函数（如 e^x， cos （x））中随机调用，以构建具有常量或状态变量的分支，作为结束分支的叶子。递归调用用于构建基于波兰符号的表达式（[2] 通过 LISP 实现，我已经适应了 Python），并制定了规则以避免除以 0 并确保数学一致性，以便每个分支在常数或传感器值叶中正确结束。从概念上讲，方程树显示为：

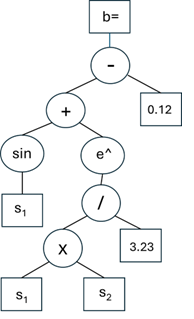
图 1.示例函数树，作者基于 [2] 提供

这导致控制器 b= sin （s1）+ e^（s1*s2/3.23）-0.12，脚本编写为： — + sin s1 e^ / * s1 s2 3.23 0.12，其中 s 表示状态变量。乍一看可能令人困惑，但写出几个例子将澄清这种方法。

构建了整整一代的树后，然后在整个环境中运行每棵树以评估性能。然后，根据获得的奖励对树木的控制性能进行排名。如果未达到预期的性能，则保留性能最佳的树，前 66% 的树通过交叉（交换两棵树的元素）、剪切和增长（替换树的一个元素）、收缩（用常量替换树元素）或重新参数化（替换树中的所有常数）进行突变 [2]。这使得利用最有前途的解决方案成为可能。为了继续探索解决方案空间，性能低下的解决方案将被随机的新树替换。然后，每一代连续的个体都是随机新个体和性能最佳解决方案的复制或突变的混合体。

根据环境中的随机起始位置对树木进行测试。为了防止“幸运”的起始状态使结果出现偏差（类似于模型的过度拟合），将针对一批不同的随机起始状态对树进行测试。

遗传编程的超参数包括：

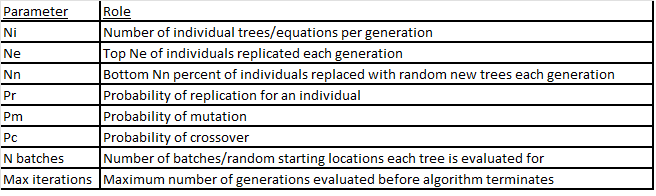
表 1.Hyperparamters for Genetic Progamming Algorthim

注释的代码可以在 github 上找到。请注意，我是一个业余编码员，我的代码很笨拙。希望它至少具有足够的可读性以理解我的方法，尽管有任何非pythonic或通常糟糕的编码实践。

三、评估方法

两种算法都在两种不同的体育馆环境中进行了评估。首先是体育馆基础提供的简单的摆锤环境。倒摆是一个简单的非线性动力学问题。动作空间是一个连续的扭矩，可以施加到摆锤上。观测空间与状态相同，是 x，y 坐标和角速度。目标是保持钟摆直立。第二个是同一个体育馆，但在观察中添加了随机噪声。噪声是正常的，平均值为 0，方差为 0.1，以模拟真实的传感器测量。

RL 开发中最重要的部分之一是设计适当的奖励函数。虽然有许多算法可以解决给定的 RL 问题，但为这些算法定义适当的优化奖励是使给定算法成功解决特定问题的关键步骤。我们的奖励需要允许我们比较两种不同 RL 方法的结果，同时确保每种方法都朝着其目标前进。在这里，对于每条轨迹，我们跟踪累积奖励和平均奖励。为了简化此操作，我们让每个环境运行固定数量的时间步长，并根据代理在每个时间步距目标状态的距离来获得负奖励。Pendulum 健身房以这种方式开箱即用——在 200 个时间步长处截断，并根据钟摆离直立的距离进行负奖励，最大奖励为 0，在每个时间步长强制执行。我们将使用平均奖励来比较这两种方法。

我们的目标是评估每个 RL 框架的收敛速度。我们将使用 AWS Sagemaker Experiments 来实现此目的，它可以按迭代或 CPU 时间自动跟踪跨运行的指标（例如当前奖励）和参数（例如活动的 hyperparmeters）。虽然这种监视可以通过 python 工具完成，但 Experiments 提供了运行参数和性能的简化跟踪和索引以及计算资源的复制。为了设置实验，我采用了 AWS 提供的示例。SAC 和 GP 算法首先在本地 Jupyter 笔记本中进行评估，然后上传到 git 存储库。每种算法都有自己的存储库和 Sagemaker 笔记本。存储运行参数以帮助对运行进行分类，并跟踪不同实验设置的性能。对于我们的情况，运行指标是奖励和状态向量，是我们想要测量以比较两种算法的因变量。实验会自动将 CPU 时间和迭代记录为自变量。

通过这些实验，我们可以比较冠军（一种成熟、成熟的 RL 算法，如 SAC）与竞争者的性能，竞争者是一种鲜为人知的方法，由业余编码员编码，没有接受过正式的 RL 或 Python 训练。该实验将深入了解为复杂非线性系统开发控制器的不同方法。在下一部分中，我们将回顾和讨论结果和可能的后续行动。

第一个实验是默认的摆锤体育馆，算法试图确定要应用的正确扭矩以保持摆锤倒置。它在固定时间后结束，并根据钟摆离垂直的距离给予负奖励。在运行 Sagemaker 实验之前，SAC 和 GP 算法都在我的本地计算机上运行，以验证收敛性。在实验中运行可以更好地跟踪可比的计算时间。计算时间与每次迭代的平均奖励的结果如下：

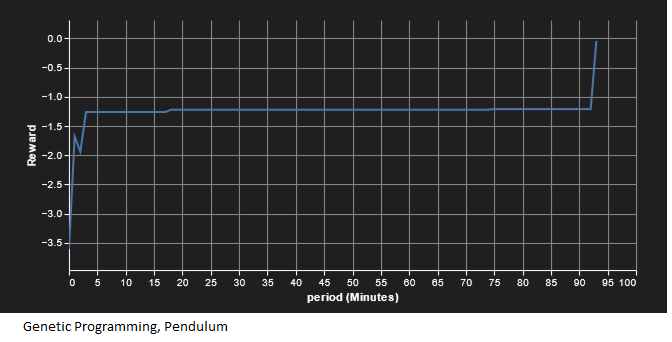
由作者提供

我们看到，尽管GP是一种不太成熟的算法，但它得出的解决方案的计算要求远低于SAC。在完成本地运行的过程中，SAC 似乎需要大约 400,000 次迭代才能收敛，需要几个小时。对本地实例化进行编程，以存储整个训练过程中 SAC 进度的记录;有趣的是，SAC似乎从学习如何将钟摆向顶部移动到学习如何保持钟摆不动，然后将这些结合起来，这可以将奖励的下降解释为SAC学习保持钟摆稳定的时间。在 GP 中，我们看到奖励的单调增加是分步进行的。这是因为性能最佳的函数树始终被保留，因此在计算出更好的控制器之前，最佳奖励保持稳定。

第二个实验是将高斯噪声（0,0.1）添加到状态测量中。我们看到的结果与无噪声情况相似，只是收敛时间更长。结果如下所示;同样，GP 的表现优于 SAC。

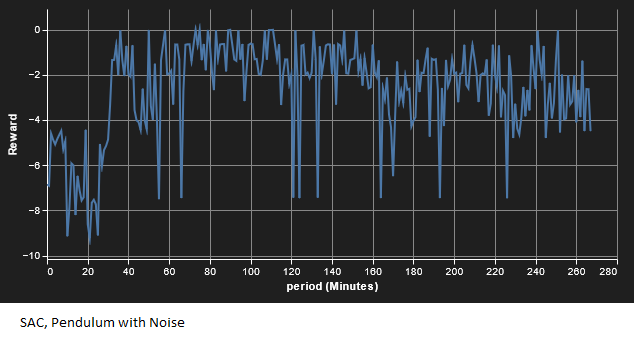
由作者提供

在这两种情况下，我们都看到 GP 的执行速度比 SAC 快（与上一个示例一样，SAC 确实在本地收敛，我只是不想为 AWS 支付计算时间！然而，正如你们中的许多人无疑已经注意到的那样，无论是在机器学习还是物理系统方面，这都是一个非常基本的比较。例如，超参数优化可能会导致不同的结果。尽管如此，对于竞争者算法来说，这是一个有希望的开始，并表明它值得进一步研究。