文章链接:https://arxiv.org/pdf/2407.05000
亮点直击
- 提出了 LoRA-GA,一种新颖的 LoRA 初始化方法,通过近似低秩矩阵的梯度与全权重矩阵的梯度来加速收敛。
- 确定了在非零初始化下的缩放因子,该因子确保适配器输出的方差不受适配器的秩和输入维度的影响。
- 通过广泛的实验验证了 LoRA-GA,证明了与原版 LoRA 相比,其性能显著提升且收敛速度更快。具体而言,LoRA-GA 在 T5-Base 的 GLUE 子集上比 LoRA 提高了 5.69%,在 Llama 2-7B 上在 MT-bench、GSM8K 和 HumanEval 上分别提高了 0.34%、11.52% 和 5.05%,同时实现了高达 2-4 倍的收敛速度提升。
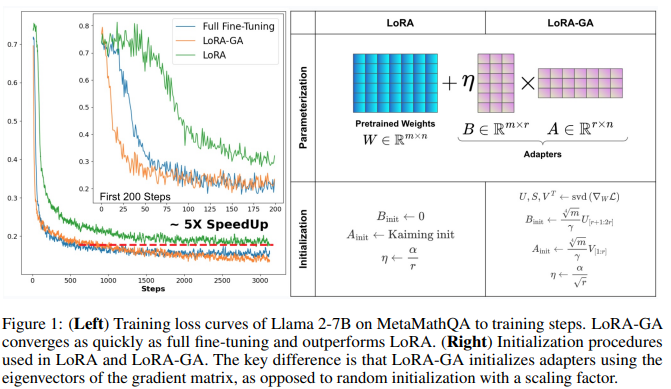
微调大规模预训练模型在计算和内存成本方面是非常昂贵的。LoRA 作为最流行的参数高效微调 (PEFT) 方法之一,通过微调一个参数显著更少的辅助低秩模型,提供了一种成本有效的替代方案。尽管 LoRA 显著减少了每次迭代的计算和内存需求,但大量实证证据表明,与完全微调相比,它的收敛速度明显较慢,最终导致总体计算增加且测试性能往往较差。本文对 LoRA 的初始化方法进行了深入研究,并表明细致的初始化(不改变架构和训练算法)可以显著提高效率和性能。本文引入了一种新颖的初始化方法,LoRA-GA(带梯度近似的低秩适应),该方法在第一步将低秩矩阵乘积的梯度与完全微调的梯度对齐。广泛实验表明,LoRA-GA 达到了与完全微调相当的收敛速度(因此显著快于原版 LoRA 及其他各种最新改进方法),同时达到相当或更好的性能。例如,在 T5-Base 的 GLUE 数据集子集上,LoRA-GA 平均比 LoRA 提高了 5.69%。在更大的模型如 Llama 2-7B 上,LoRA-GA 在 MT-bench、GSM8K 和 Human-eval 上分别表现出 0.34%、11.52% 和 5.05% 的性能提升。此外,与原版 LoRA 相比,收敛速度提高了 2-4 倍,验证了其在加速收敛和提升模型性能方面的有效性。
方法
本节分析了 LoRA 的初始化并介绍了LoRA-GA。它包括两个关键组件,分别检查每个组件,并介绍它们在 LoRA-GA 中的整合。
- 近似全微调的梯度方向
- 确保初始化过程中的秩和Scale稳定性。
原版 LoRA 回顾
LoRA 的结构 基于微调更新是低秩的假设,LoRA提出了使用两个低秩矩阵的乘积来表示原始矩阵 W 的增量部分。在这里,W 是模型中线性层的权重矩阵。例如,在transformers中,它可以是自注意力层的 Q、K、V 或 O 矩阵,或者是 MLP 层的权重矩阵。具体来说,LoRA 具有以下数学形式。
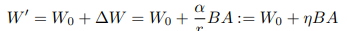
其中 W ′ , W 0 ∈ R m × n W', W_0 \in \mathbb{R}^{m \times n} W′,W0∈Rm×n, B ∈ R m × r B \in \mathbb{R}^{m \times r} B∈Rm×r,以及 A ∈ R r × n A \in \mathbb{R}^{r \times n} A∈Rr×n,且 r ≪ min ( m , n ) r \ll \min(m, n) r≪min(m,n)。 W 0 W_0 W0 是预训练的权重矩阵,在微调过程中保持冻结,而 A A A 和 B B B 是可训练的。
LoRA 的初始化
在 LoRA 的默认初始化方案中,矩阵 A A A 使用 Kaiming 均匀分布初始化,而矩阵 B B B初始化为全零。因此, B A = 0 BA = 0 BA=0 并且 W 0 ′ = W 0 W'_0 = W_0 W0′=W0,确保初始参数不变。
如果附加项 Δ W = η B A \Delta W = \eta BA ΔW=ηBA 最初是非零的(例如 [37]),则可以调整冻结参数以确保初始参数不变。这可以表示为:
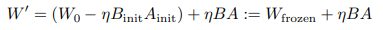
其中 W frozen = W 0 − η B init A init W_{\text{frozen}} = W_0 - \eta B_{\text{init}} A_{\text{init}} Wfrozen=W0−ηBinitAinit 是冻结的,在这种情况下, B B B 和 A A A 是可训练的。
梯度近似
目标是确保第一步更新 Δ ( η B A ) \Delta(\eta BA) Δ(ηBA) 近似于权重更新的方向 Δ W \Delta W ΔW,即 Δ ( η B A ) ≈ ζ Δ W \Delta(\eta BA) \approx \zeta \Delta W Δ(ηBA)≈ζΔW,其中 ζ \zeta ζ 是某个非零正常数。后面将讨论如何选择 ζ \zeta ζ,现在可以将 ζ \zeta ζ 视为一个固定常数。
考虑学习率为 λ \lambda λ 的梯度下降步骤, A A A 和 B B B 的更新分别为 Δ A = λ ∇ A L ( A init ) \Delta A = \lambda \nabla_A L(A_{\text{init}}) ΔA=λ∇AL(Ainit) 和 Δ B = λ ∇ B L ( B init ) \Delta B = \lambda \nabla_B L(B_{\text{init}}) ΔB=λ∇BL(Binit)。假设学习率 λ \lambda λ 很小,第一步更新的 η B A \eta BA ηBA可以表示为:
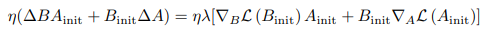
为了衡量其对全微调中权重更新的缩放近似质量 ζ Δ W = ζ λ ∇ W L ( W 0 ) \zeta \Delta W = \zeta \lambda \nabla_W L(W_0) ζΔW=ζλ∇WL(W0),使用这两个更新之间差异的 Frobenius 范数作为标准:

Lemma 3.1. 假设损失函数是
L
L
L 并且
y
=
W
′
x
=
(
W
0
+
η
B
A
)
x
y = W'x = (W_0 + \eta BA)x
y=W′x=(W0+ηBA)x,其中
y
y
y 是一层的输出,
x
x
x 是输入,那么
A
A
A 和
B
B
B 的梯度是
W
′
W'
W′ 梯度的线性映射:
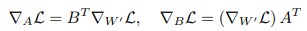
值得注意的是,在训练开始时,LoRA 中的 ∇ W ′ L \nabla_{W'}L ∇W′L 和全微调中的 $\nabla_W L $ 是相等的。通过将Lemma 3.1 中的梯度代入公式 1,可以将标准重写如下:
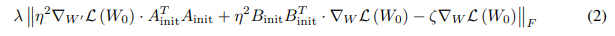
这一标准评估了适配器的梯度在多大程度上近似于全微调的梯度方向,最小化它可以使 LoRA 的梯度更接近全微调的梯度,并带有缩放因子 ζ \zeta ζ:
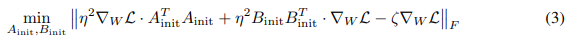
定理 3.1. 对于给定 ζ \zeta ζ 的方程 3 中的优化问题,如果 ∇ W L \nabla_W L ∇WL 的奇异值分解 (SVD) 是 ∇ W L = U S V T \nabla_W L = USV^T ∇WL=USVT,其解为:
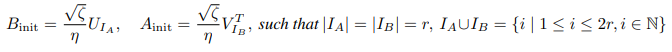
其中 I A I_A IA 和 I B I_B IB 是索引集。
定理 3.1 为给定特定 ζ \zeta ζ 的 A init A_{\text{init}} Ainit 和 B init B_{\text{init}} Binit提供了适当的初始化方案。 ζ \zeta ζ 的选择会影响更新 η B A \eta BA ηBA 的缩放,具体的 $\zeta $ 选择下节讨论。
Scale稳定性
受到 rsLoRA和 Kaiming 初始化的启发,定义了稳定性:
定义 3.1. 当 d out , d in , r → ∞ d_{\text{out}}, d_{\text{in}}, r \to \infty dout,din,r→∞ 时,适配器 η B A \eta BA ηBA 显示出两种不同类型的Scale稳定性:
- 前向稳定性:如果适配器的输入是独立同分布 (i.i.d.),且其 2 阶矩为 Θ r , d out , d in ( 1 ) \Theta_{r,d_{\text{out}},d_{\text{in}}}(1) Θr,dout,din(1),则输出的 2 阶矩保持为 Θ r , d out , d in ( 1 ) \Theta_{r,d_{\text{out}},d_{\text{in}}}(1) Θr,dout,din(1)。
- 后向稳定性:如果相对于适配器输出的损失梯度为 Θ r , d out , d in ( 1 ) \Theta_{r,d_{\text{out}},d_{\text{in}}}(1) Θr,dout,din(1),则相对于输入的梯度保持为 Θ r , d out , d in ( 1 ) \Theta_{r,d_{\text{out}},d_{\text{in}}}(1) Θr,dout,din(1)。
定理 3.2. 给定定理 3.1 中提出的初始化方案,假设 A init A_{\text{init}} Ainit 和 $ B_{\text{init}}$ 中的正交向量是从 R d in \mathbb{R}^{d_{\text{in}}} Rdin 和 R d out \mathbb{R}^{d_{\text{out}}} Rdout 中的单位球面上随机选择的,并且这些向量彼此正交,且 $ \eta = \Theta_{r,d_{\text{out}},d_{\text{in}}}(1/\sqrt{r}) ,如 r s L o R A 所建议的。在这些条件下,适配器在 ,如 rsLoRA 所建议的。在这些条件下,适配器在 ,如rsLoRA所建议的。在这些条件下,适配器在\zeta = \Theta_{r,d_{\text{out}},d_{\text{in}}} \left( \sqrt{d_{\text{out}}/r^2} \right)$ 时是前向Scale稳定的,且在 ζ = Θ r , d out , d in ( d in / r 2 ) \zeta = \Theta_{r,d_{\text{out}},d_{\text{in}}} \left( \sqrt{d_{\text{in}}/r^2} \right) ζ=Θr,dout,din(din/r2) 时是后向Scale稳定的。
类似于 Kaiming 初始化的结果,观察到 ζ = Θ r , d out , d in ( d out / r 2 ) \zeta = \Theta_{r,d_{\text{out}},d_{\text{in}}} \left( \sqrt{d_{\text{out}}/r^2} \right) ζ=Θr,dout,din(dout/r2) 或 ζ = Θ r , d out , d in ( d in / r 2 ) \zeta = \Theta_{r,d_{\text{out}},d_{\text{in}}} \left( \sqrt{d_{\text{in}}/r^2} \right) ζ=Θr,dout,din(din/r2) 各自都有效。对于本文中介绍的所有模型,任一形式均确保收敛。因此,在所有后续实验中,采用 ζ = Θ r , d out , d in ( d out / r 2 ) \zeta = \Theta_{r,d_{\text{out}},d_{\text{in}}} \left( \sqrt{d_{\text{out}}/r^2} \right) ζ=Θr,dout,din(dout/r2)。
LoRA-GA 初始化
结合梯度近似和稳定Scale组件,提出了 LoRA-GA 初始化方法。首先,使用定理 3.1 的解来初始化 A init A_{\text{init}} Ainit 和 B init B_{\text{init}} Binit。然后,根据定理 3.2 确定缩放因子 ζ \zeta ζ 以确保秩和Scale的稳定性。因此,基于定理 3.1 和 3.2,本文提出了一种新颖的初始化方法,即 LoRA-GA。
LoRA-GA:采用 η = α r \eta = \frac{\alpha} {\sqrt r} η=rα 和 ζ = α 2 γ 2 d out / r 2 \zeta = \frac{\alpha^2} {\gamma^2} {\sqrt{d_{\text{out}}/r^2}} ζ=γ2α2dout/r2,其中 γ \gamma γ 是一个超参数。定义索引集 I A = { i ∣ 1 ≤ i ≤ r , i ∈ N } I_A = \{i \mid 1 \leq i \leq r, i \in \mathbb{N} \} IA={i∣1≤i≤r,i∈N}和 I B = { i ∣ r + 1 ≤ i ≤ 2 r , i ∈ N } I_B = \{i \mid r + 1 \leq i \leq 2r, i \in \mathbb{N} \} IB={i∣r+1≤i≤2r,i∈N}。将 ∇ W L \nabla_W L ∇WL 的奇异值分解 (SVD) 表示为 ∇ W L = U S V T \nabla_W L = USV^T ∇WL=USVT。初始化如下:
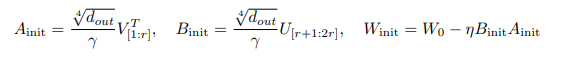
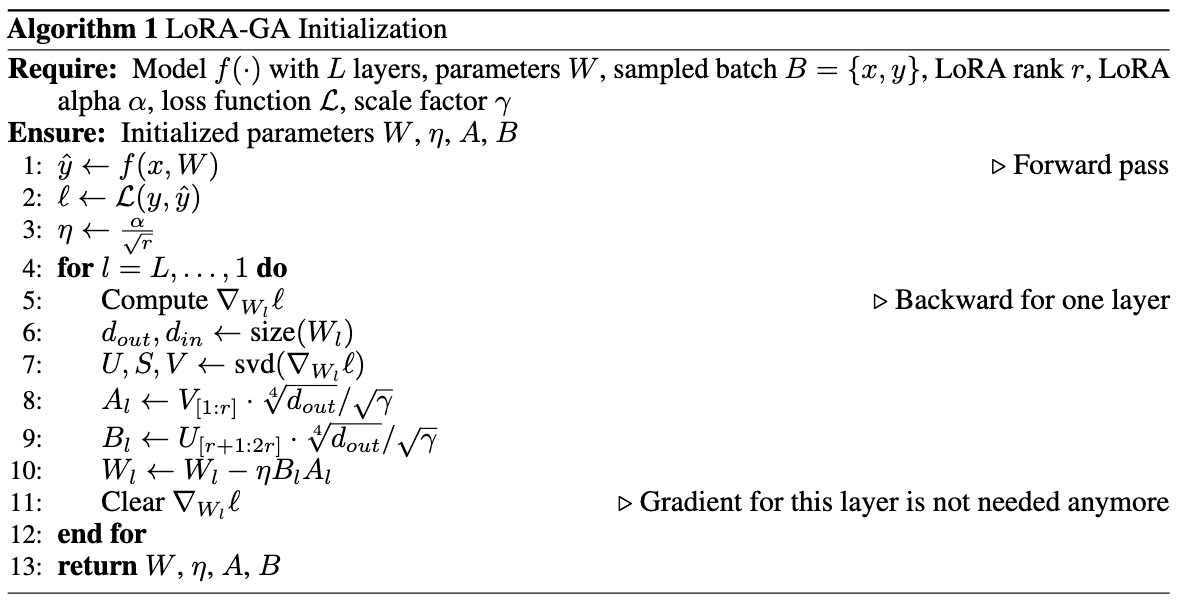
为了在 LoRA-GA 初始化期间节省 GPU 内存,采用了类似于 [39] 的技术。通过挂钩到 PyTorch 的反向传播过程,逐层计算梯度,并立即丢弃计算出的梯度。这确保了内存使用保持在 O ( 1 ) O(1) O(1) 级别,而不是 O ( L ) O(L) O(L),其中 L L L 是层的数量。这种方法使得初始化阶段的内存消耗低于后续 LoRA 微调阶段。算法见下算法 1。如果采样的批量大小很大,还可以使用梯度累积进一步节省内存,如下算法 2 所示。

实验
本节中,评估了 LoRA-GA 在各种基准数据集上的性能。首先,使用 T5-Base 模型 在 GLUE 数据集 的一个子集上评估自然语言理解 (NLU) 能力。随后,使用 Llama 2-7B 模型评估对话、数学推理和编码能力。最后,进行消融研究以证明本文方法的有效性。
Baselines 将 LoRA-GA 与几个基线进行比较,以展示其有效性:
- 完全微调 (Full-Finetune) :对模型进行全参数微调,这需要最多的资源。
- 原版 LoRA (Vanilla LoRA) :通过在线性层中插入低秩矩阵乘积 B A BA BA对模型进行微调。 A A A 使用 Kaiming 初始化,而 B B B 初始化为零。
- 具有原始结构的 LoRA 变体:包括几个保留原始 LoRA 结构的方法:
- rsLoRA :引入新的缩放因子以稳定 LoRA 的Scale。
- LoRA+ :使用不同的学习率更新 LoRA 中的两个矩阵。
- PiSSA :建议在训练开始时对权重矩阵 W W W 进行 SVD,并基于具有较大奇异值的组件初始化 A A A 和 B B B。
- 具有修改结构的 LoRA 变体:包括修改原始 LoRA 结构的方法:
- DoRA :通过添加可学习的幅度来增强模型的表达能力。
- AdaLoRA :在微调过程中使用 SVD 动态剪枝不重要的权重,在固定参数预算内允许更多的秩分配给重要区域。
自然语言理解实验
模型与数据集 在 GLUE 基准的多个数据集上微调 T5-Base 模型,包括 MNLI、SST-2、CoLA、QNLI 和 MRPC。使用准确率作为主要指标,在开发集上评估性能。
实现细节 使用提示微调 (prompt tuning) 方法对 T5-Base 模型进行 GLUE 基准的微调。这涉及将标签转换为令牌(例如,“positive” 或 “negative”),并使用这些令牌的归一化概率作为分类的预测标签概率。每个实验使用 3 个不同的随机种子进行,并报告平均性能。
结果
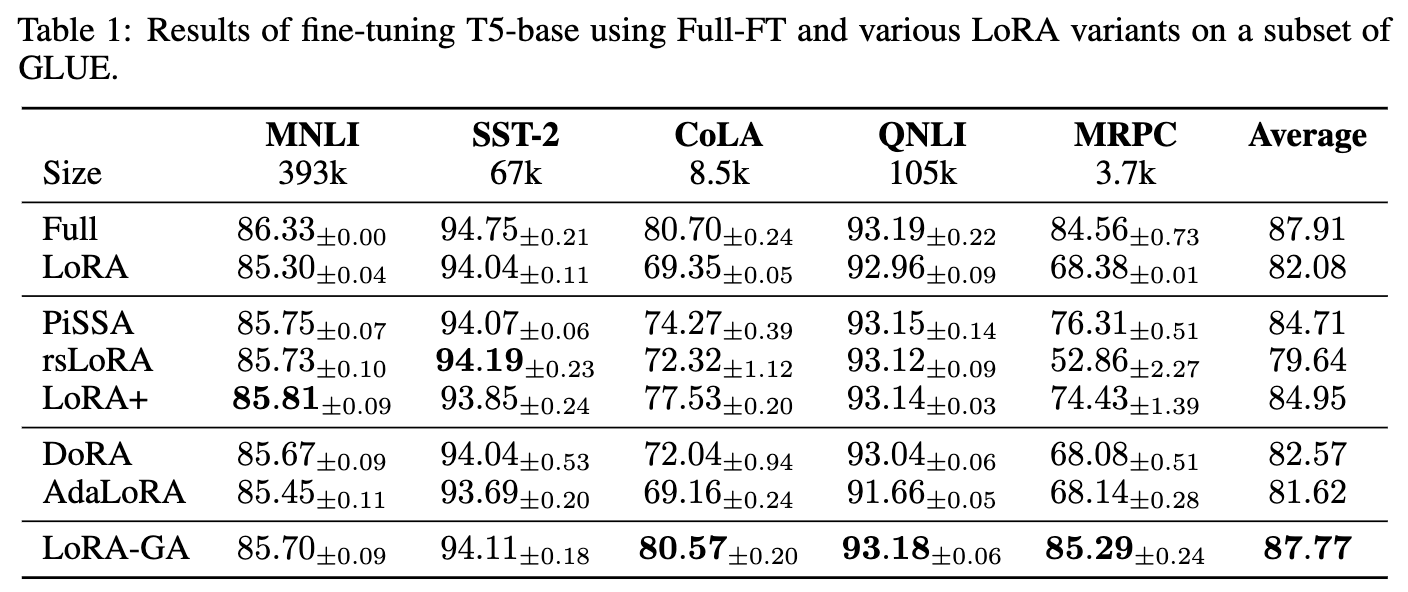
如下表 1 所示,LoRA-GA 一直优于原版 LoRA 和其他基线方法,取得了与完全微调相当的性能。特别是,LoRA-GA 在较小的数据集如 CoLA 和 MRPC 上表现突出,展示了其在有限训练数据下更快收敛和有效利用的能力。
大语言模型实验
模型与数据集 为了评估 LoRA-GA 的可扩展性,在三个任务上训练了 Llama 2-7B 模型:对话、数学和代码。
- 对话 (Chat) :在 WizardLM的 52k 子集上训练模型,过滤掉以“作为 AI”或“对不起”开头的回应。在 MT-Bench 数据集上测试模型,该数据集由 80 个多轮问题组成,旨在评估大语言模型的多个方面。回答的质量由 GPT-4 进行评判,报告第一次回答的得分。
- 数学 (Math) :在 MetaMathQA 的 100k 子集上训练模型,这个数据集从其他数学指令调整数据集(如 GSM8K和 MATH)中引导而来,具有更高的复杂性和多样性。选择从 GSM8K 训练集中引导的数据并应用过滤。准确率在 GSM8K 评估集上报告。
- 代码 (Code) :在 Code-Feedback的 100k 子集上训练模型,这是一个高质量的代码指令数据集,去除代码块后的解释。模型在 HumanEval上进行测试,该数据集包含 180 个 Python 任务,报告 PASS@1 指标。
实现细节 本文的模型使用标准的监督学习进行语言建模训练。输入提示的损失设置为零。每个实验使用 3 个不同的随机种子进行,并报告这些运行的平均性能。
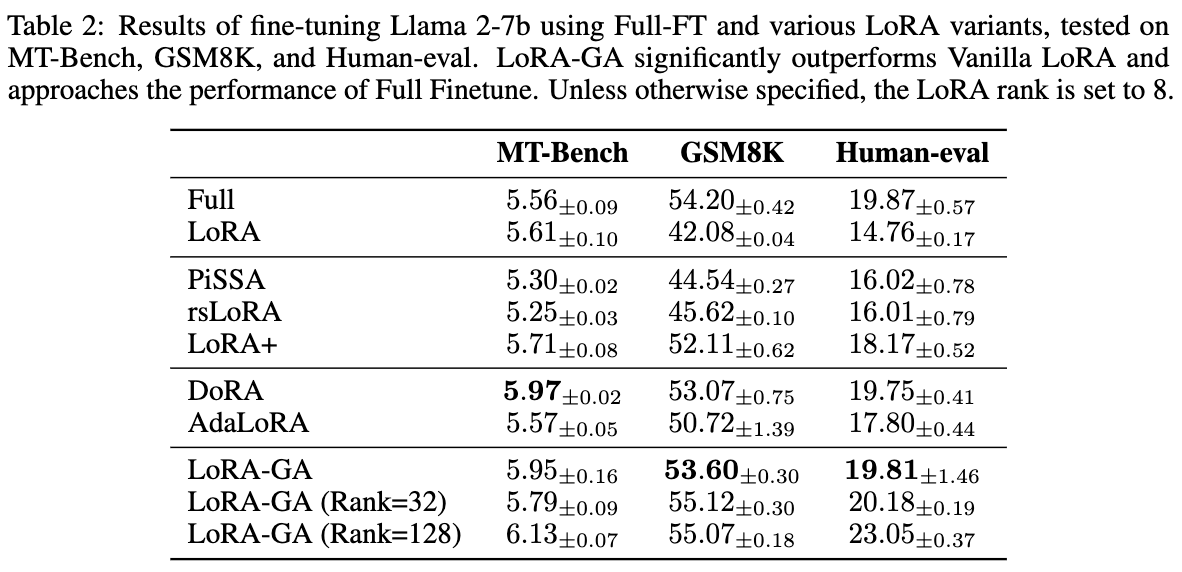
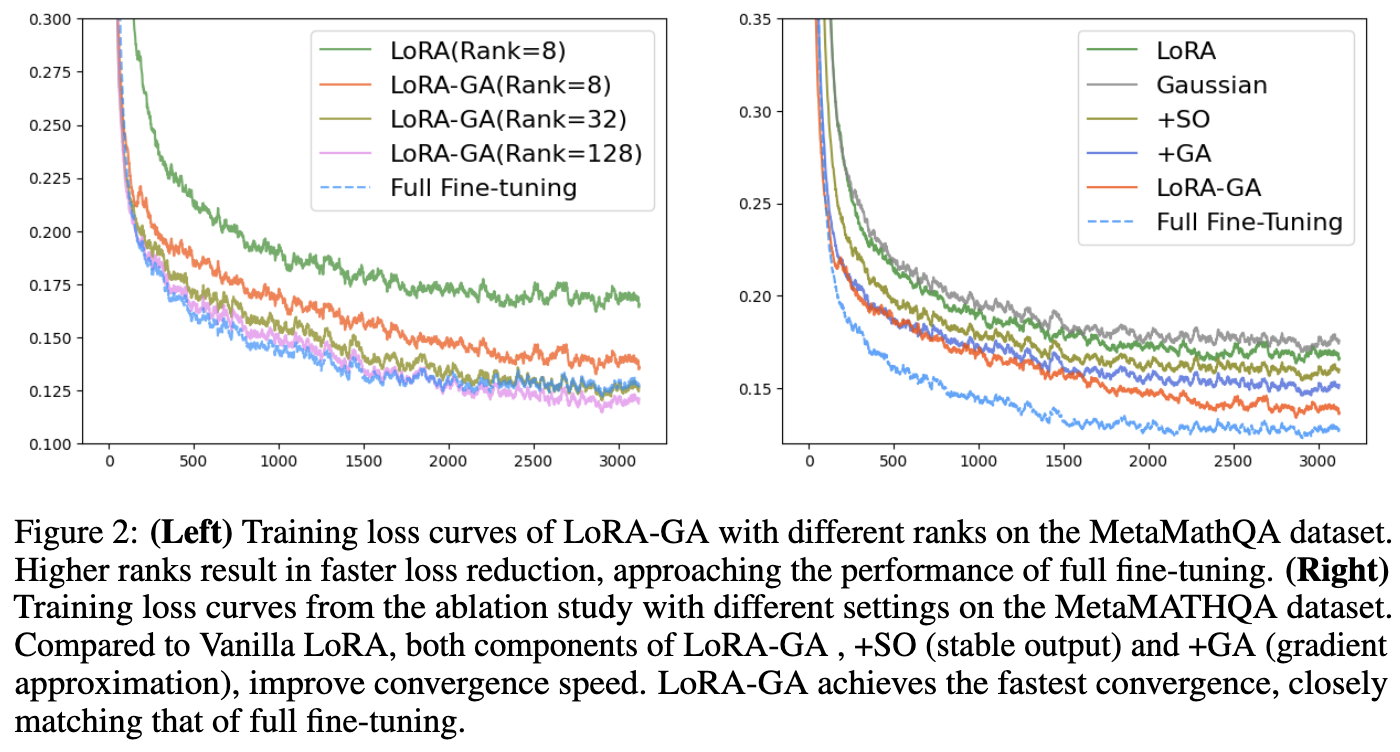
结果 结果如下表 2 所示,表明 LoRA-GA 优于或与其他方法相当,包括完全微调。具体而言,LoRA-GA 在 GSM8K 和 Human-eval 数据集上表现出色,突显了其在处理具有更高复杂性和多样性的任务方面的有效性。在 MT-Bench 上,LoRA-GA 也展现了竞争力的性能,尽管略微落后于 DoRA。然而,LoRA-GA 在参数较少且大约仅需 DoRA 70% 的训练时间的情况下实现了这些性能。此外,如下图 2(左)所示,本文的方法在收敛速率上显著快于原版 LoRA,其收敛速率与完全微调相当。
影响秩
将 GSM8K 和 Human-eval 数据集上的性能差异(与完全微调相比)主要归因于低秩近似所带来的表示限制。为了解决这个问题,尝试了更高的秩设置,具体为秩=32 和秩=128。发现表明,LoRA-GA 在不同秩设置下保持稳定,并且在某些情况下,甚至超越了完全微调的性能。如图 2(左)所示,初始化方法下更高的秩也导致了与完全微调相似的损失曲线。
消融研究
研究者们进行了消融研究,以评估 LoRA-GA 中非零初始化、稳定输出和梯度近似的贡献,使用了五种不同的实验设置。每个设置的详细信息见下表 3。

消融结果
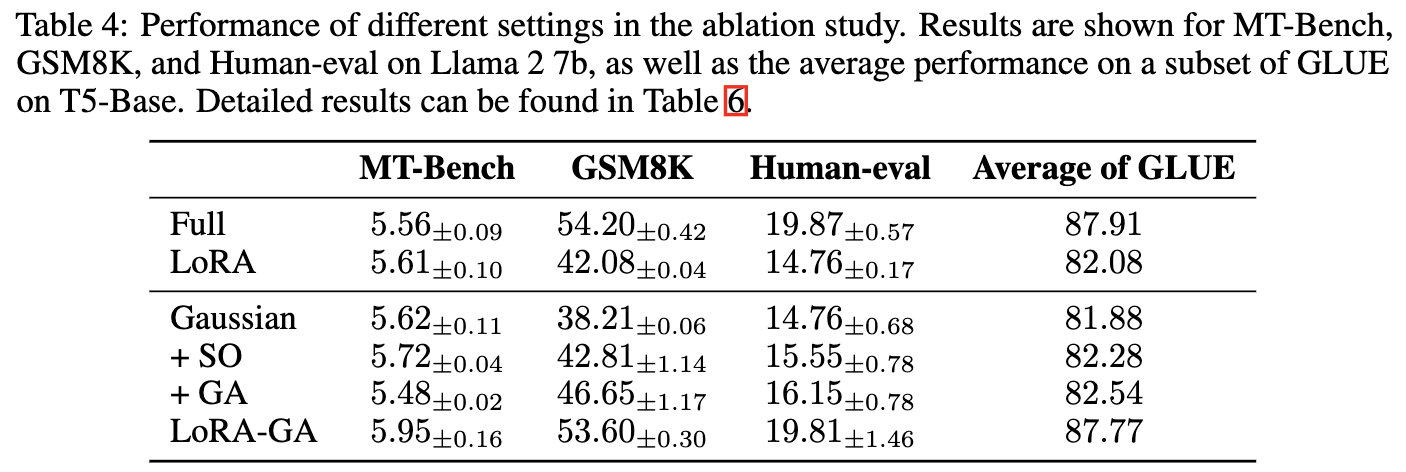
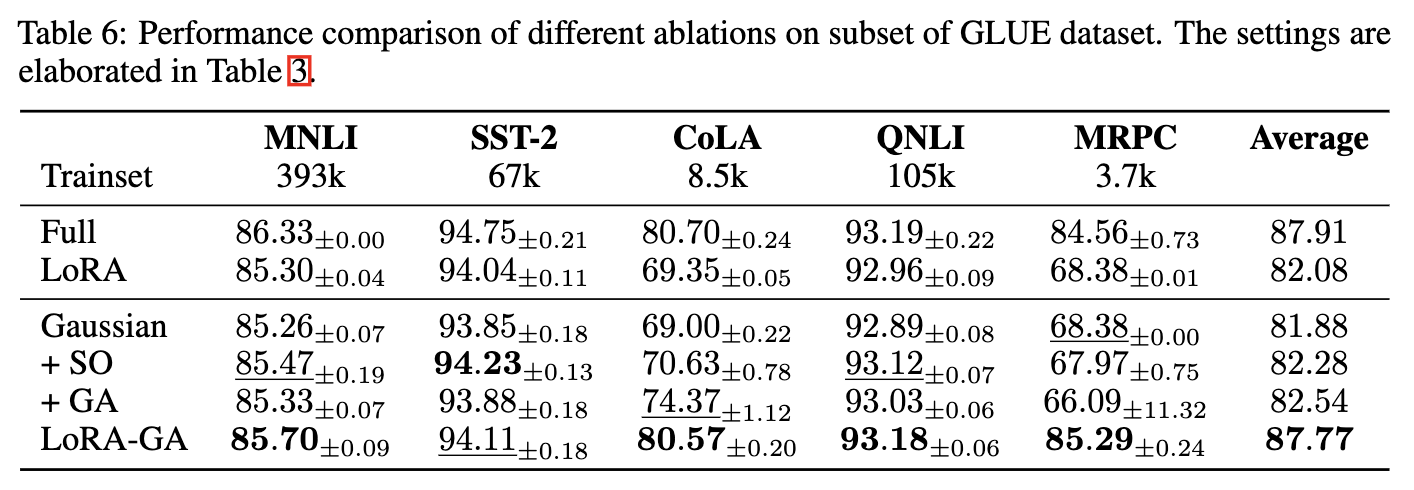
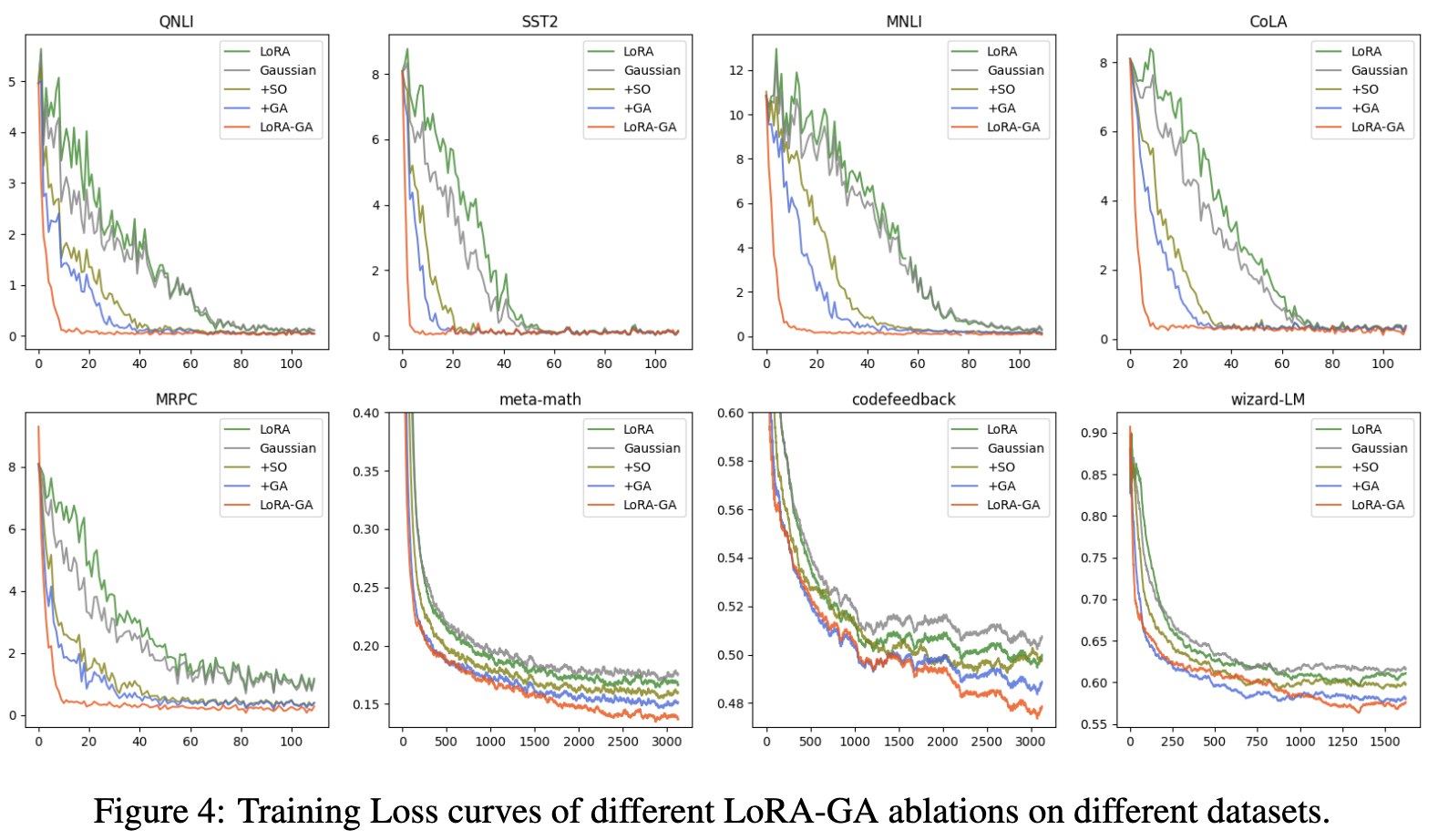
结果如下表 4 和表 6 所示。对于小型和大型模型,观察到,仅将 LoRA 的初始化更改为高斯初始化并未带来性能提升,甚至可能导致轻微的性能下降。然而,当与“+SO”(稳定输出)或“+GA”(梯度近似)结合使用时,性能优于 LoRA。LoRA-GA,结合了这两种技术,表现优于其他方法。如上图 2(左)和下图 4 所示,+SO 和 +GA 也提高了收敛速度,并且当两者结合时,训练损失曲线甚至更接近完全微调的曲线。这表明,输出稳定性和梯度近似都对 LoRA 的改进有所贡献,各自解决了模型性能的不同方面。
内存成本和运行时间
研究者们在单个 RTX 3090 24GB GPU、128 核 CPU 和 256GB RAM 上对 LoRA-GA 进行了基准测试。如下表 5 所示,本文的新方法的内存消耗不超过 LoRA 训练时的内存消耗,表明没有额外的内存需求。此外,与后续的微调过程相比,这项操作的时间成本相对微不足道。例如,在 Code-Feedback 任务中,训练过程大约花费了 10 小时,而初始化仅需约 1 分钟,这一时间差异可以忽略不计。

结论
本文提出了一种用于低秩适应(LoRA)的新初始化方案,旨在加速其收敛。通过研究 LoRA 的初始化方法和更新过程,开发了一种新初始化方法——LoRA-GA,该方法从第一步起就将低秩矩阵乘积的梯度近似为完全微调的梯度。
通过大量实验,展示了 LoRA-GA 能够实现与完全微调相当的收敛速度,同时提供类似或更优的性能。由于 LoRA-GA 仅修改了 LoRA 的初始化,而未改变架构或训练算法,它提供了一种高效且易于实施的方法。此外,它还可以与其他 LoRA 变体结合使用。例如,ReLoRA 定期将适配器合并到冻结权重 W 中,这可能使 LoRA-GA 在更多步骤中展现其优势。将此作为一个有趣的未来研究方向。
参考文献
[1] LoRA-GA: Low-Rank Adaptation with Gradient Approximation