【POJ No. 3253】 围栏修复 Fence Repair

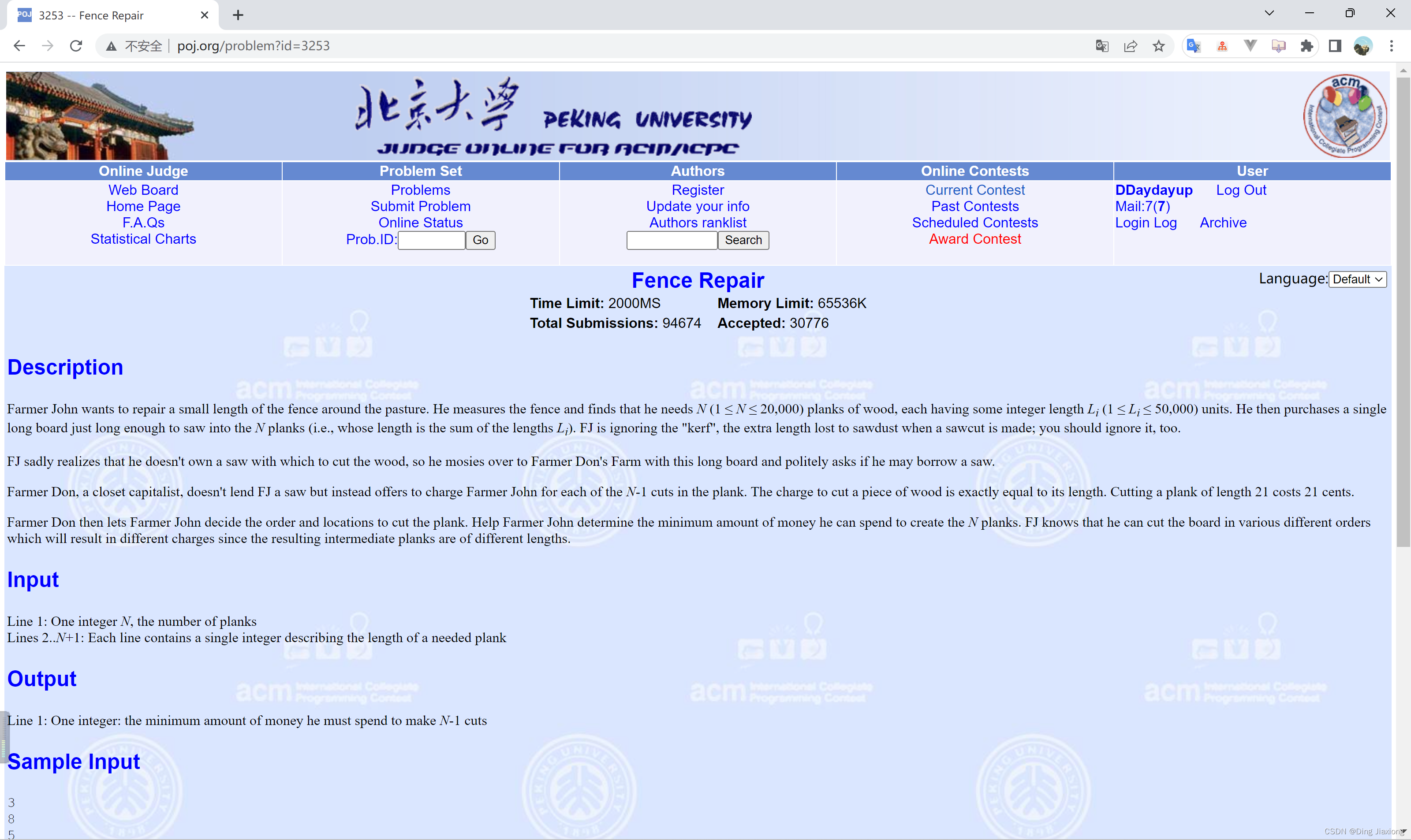
北大OJ 题目地址

这道题其实我们 之前就做过了
https://blog.csdn.net/weixin_44226181/article/details/127064923

当时我们 是在学习哈夫曼树

【题意】

约翰想修牧场周围的篱笆，需要N 块（1≤N ≤20000）木板，每块木板的长度都为Li （1≤Li ≤50000，整数）米。他购买了一块足够长的木板（长度为Li 的总和，i =1, 2,…, N ），以便得到N 块木板，切割时木屑损失的长度不计。唐向约翰收取切割费用，切割一块木板的费用与其长度相同，切割21米的木板需要21美分。唐让约翰决定切割木板的顺序和位置。约翰知道以不同的顺序切割木板，将会产生不同的费用。

请帮助约翰确定他得到N 块木板的最低花费。

【输入输出】

输入：

第1行包含整数N ，表示木板的数量。第2…N +1行，每行都包含一个所需木板的长度Li 。

输出：

一个整数，即进行N -1次切割的最低花费。

【样例】

【思路分析】

这道题类似哈夫曼树的构建方法，每次都选择两个最小的合并，直到合并为一棵树。每次合并的结果就是切割的费用。

【算法设计】

使用优先队列（最小值优先），每次都弹出两个最小值t 1 、t 2 ，=t 1 +t 2 ，sum+=t ，将t 入队，继续，直到队空。sum为所需花费。

【算法实现】

定义一个优先队列（最小值优先），输入元素入队。若队中只有一个元素，则直接累加输出即可。若队中多于一个元素，则每次都取两个最小值，累加和值，并将和值入队。

#include<iostream>
#include<cstdio>
#include<queue>

using namespace std;

int main(){
	
	long long sum;
	int n,t,t1,t2;
	while(cin>>n){
		priority_queue<int,vector<int>,greater<int> >q;
		for(int i=0;i<n;i++){
			cin >> t;//scanf("%d",&t);
			q.push(t);
		}
		sum=0;
		if(q.size()==1){
			t1=q.top();
			sum+=t1;
			q.pop();
		}
		while(q.size()>1){
			t1=q.top();
			q.pop();
			t2=q.top();
			q.pop();
			t=t1+t2;
			sum+=t;
			q.push(t);
		}
		cout << sum << endl;
	}
	
	return 0;
}