第59天,dijkstra算法的优化版本,以及Bellman_ford 算法💪💪(ง •_•)ง,编程语言:C++
目录
dijkstra(堆优化版)精讲
思路
图的存储
邻接矩阵
邻接表
本题图的存储
堆优化细节
Bellman_ford 算法精讲
何为松弛
模拟过程
Bellman_ford总结
总结
dijkstra(堆优化版)精讲
文档讲解:代码随想录dijkstra(堆优化版)精讲
思路
题目:47. 参加科学大会(第六期模拟笔试) (kamacoder.com)


之前我们使用了朴素版的dijkstra,该解法的时间复杂度为O(n^2),n为节点的数量。如果n很大的话,显然时间复杂度就会很高。
在最小生成树的问题中也有同样的问题,节点数量多的情况下prim算法的时间复杂度就会很好,因此我们推荐使用kruskal算法来进行求解。而kruskal算法就是从边出发考虑的算法。
因此当节点数量n过大的时候,我们能否对算法进行优化,从边的角度进行考虑,来降低时间复杂度呢,具体的操作,我们一步步进行。
图的存储
图的存储的主流方式有:邻接矩阵和邻接表。
邻接矩阵
邻接矩阵是使用二维数组来表示图结构。邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。

显然邻接矩阵的优点:
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
邻接矩阵的缺点:
- 遇到稀疏图,会导致申请过大的二维数组造成空间浪费且遍历边的时候需要遍历整个n * n矩阵,造成时间浪费。
邻接表
邻接表是时使用数组+链表的方式来保存图,邻接表是从边的数量来表示图,有多少边才会申请对应大小的链表。

邻接表的优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点链接情况相对容易
缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要O(V)时间,V表示某节点链接其他节点的数量。
- 实现相对复杂,不易理解
本题图的存储
由于我们考虑的是节点多,边少的情况,因此我们按照稀疏图的角度进行分析。在朴素版的dijkstra算法中,我们提到了三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
这三部曲是套在一个for循环当中的,每一次循环就是确定一个节点,这是从节点的角度来解决问题的。同时第一步选择源点又需要for循环遍历minDist数组来寻找最近的节点,因此有两层for循环。
for (int i = 1; i <= n; i++) { // 遍历所有节点,第一层for循环
int minVal = INT_MAX;
int cur = 1;
// 1、选距离源点最近且未访问过的节点 , 第二层for循环
for (int v = 1; v <= n; ++v) {
if (!visited[v] && minDist[v] < minVal) {
minVal = minDist[v];
cur = v;
}
}
visited[cur] = true; // 2、标记该节点已被访问
// 3、第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (int v = 1; v <= n; v++) {
if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {
minDist[v] = minDist[cur] + grid[cur][v];
}
}
}那么如果我们想办法从边的角度出发,在处理三部曲里的第一步( 选源点到哪个节点近且该节点未被访问过)的时候 ,我们可以不用去遍历所有节点了。
方法是将边(带权值)加入到小顶堆(利用堆来自动排序),那么每次我们从堆顶里取出边自然就是距离源点最近的节点所在的边。这样我们就不需要两层for循环来寻找最近的节点了。
接下来我们来进行代码实现:
对于边稀疏图我们采用邻接表的方式来进行图的存储。
vector<list<int>> grid(n + 1);这是一般的邻接表的代码,但本题中我们还需要保存边的权值,因此数据结构还需要扩展一位。
vector<list<pair<int,int>>> grid(n + 1);
当然如果我们不习惯使用pair结构,我们还可以自己定义一个结构体来取代pair,如下所示:
struct Edge {
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
vector<list<Edge>> grid(n + 1); // 邻接表堆优化细节
思路依然是dijkstra三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
只不过我们这次循环是从边的角度进行:
第一步,选源点到哪个节点近且该节点未被访问过。我们要选择距离源点最近的节点(即:该边的权值最小),所以我们需要一个小顶堆来帮我们对边的权值进行排序,每次从小顶堆堆顶取边就是权值最小的边。
C++中的小顶堆,可以用优先级队列实现,代码如下:
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 优先队列中存放 pair<节点编号,源点到该节点的权值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;有了小顶堆自动对边的权值排序,那我们只需要直接从 堆里取堆顶元素(小顶堆中,最小的权值在上面),就可以取到离源点最近的节点了 (未访问过的节点,不会加到堆里进行排序)
所以三部曲中的第一步,我们不用 for循环去遍历,直接取堆顶元素:
// pair<节点编号,源点到该节点的权值>
pair<int, int> cur = pq.top(); pq.pop();第二步(该最近节点被标记访问过)这个就是将节点做访问标记,和朴素dijkstra一样,代码如下:
// 2. 第二步,该最近节点被标记访问过
visited[cur.first] = true;第三步,同样需要修改minDist数组,同时还要加入新的边。
遍历边的方式为:
for (Edge edge : grid[cur.first]) cur.first 就是cur节点编号, 参考上面pair的定义: pair<节点编号,源点到该节点的权值>
接着就是更新非访问节点到源点的距离,代码实现和朴素版本一样,只是加了一个堆。
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
// cur指向的节点edge.to,这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}总结来说和朴素版本的dijkstra的思路是一样的主要区别有两点:
- 邻接表的表示方式不同
- 使用优先级队列(小顶堆)来对新链接的边排序
代码:
#include <iostream>
#include <vector>
#include <list>
#include <queue>
#include <climits>
using namespace std;
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 定义一个结构体来表示带权重的边
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
// 优先队列中存放 pair<节点,源点到该节点的权值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
// 初始化队列,源点到源点的距离为0,所以初始为0
pq.push(pair<int, int>(start, 0));
minDist[start] = 0; // 起始点到自身的距离为0
while (!pq.empty()) {
// 1. 第一步,选源点到哪个节点近且该节点未被访问过 (通过优先级队列来实现)
// <节点, 源点到该节点的距离>
pair<int, int> cur = pq.top(); pq.pop();
if (visited[cur.first]) continue;
// 2. 第二步,该最近节点被标记访问过
visited[cur.first] = true;
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
// cur指向的节点edge.to,这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}
}
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
return 0;
}本算法的时间复杂度为O(ElogE),空间复杂度为O(N+E)。
当然本题也能够使用邻接矩阵来进行求解,但我们本身就假设了图是稀疏图的情况,因此采用邻接矩阵是一个增大时间复杂度的方式,是不可取的。
Bellman_ford 算法精讲
文档讲解:代码随想录Bellman_ford 算法精讲
题目:94. 城市间货物运输 I (kamacoder.com)


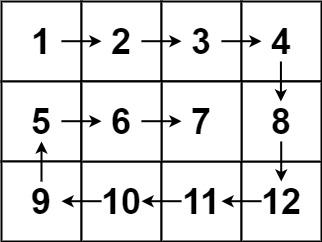
本题实际上就是最短路径问题的升级版本,加入了负权值的情况。我们知道由于dijkstra算法的特点,存在负权值的情况下,我们可能会错过更好的了路径。如下图,最好的路径应该是1-2-3-4-5这样的路径,但是dijkstra算法,一开始就会选取1-3的路径加入结果,节点3就已经会被标记了。

因此我们需要一个新的算法来解决带负权值的最短路径问题,也就是Bellman_ford算法。
Bellman_ford算法的核心思想是对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路。
何为松弛
何为松弛,又为什么是n - 1次呢,接下来我们慢慢学习。
松弛在《算法四》里叫做“放松”,在英文版里叫做“relax the edge”。但书中并没有具体解释放松是什么意思。这里我们需要举个例子,如图:

minDist[B]表示到达B节点最小权值,那么minDist[B]可以由哪些状态推出来呢。
状态一:minDist[A] + value 可以推出 minDist[B] 状态二: minDist[B]本身就有权值(可能是其他边链接的节点B例如节点C,以至于 minDist[B]记录了其他边到minDist[B]的权值)
这样我们minDist[B]的取值应该是,取最小值,也就是:
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value也就是说,如果通过A到B这条边可以获得更短的到达B节点的路径,即如果 minDist[B] > minDist[A] + value,那么我们就更新 minDist[B] = minDist[A] + value ,这个过程就叫做 “松弛” 。
换句话说“松弛“的核心代码就是这条代码:
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
//或者
minDist[B] = min(minDist[A] + value, minDist[B])这个代码其实有点像是动态规划中,进行更新的代码。实际上Bellman_ford算法,就是采用动态规划的思想,即:将一个问题分解成多个决策阶段,通过状态之间的递归关系最后计算出全局最优解。其实minDist也有点像dp数组,minDist[j]表示到达j节点的最短路径。
那么为什么是n - 1次松弛呢。这里需要我们进行Bellman_ford算法的模拟,来观察这n - 1次松弛操作是什么样的。
模拟过程
初始化:
起点为节点1,起点到起点的距离为0,所以minDist[1]初始化为0。其他节点对应的minDist初始化为max。

接下来我们对所有边进行第一次松弛,以示例给出的所有便为例:
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5边:节点5 -> 节点6,权值为-2 ,minDist[5]还是默认数值max,所以不能基于节点5去更新节点6,所以minDist数组不发生改变。

边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1

边:节点5 -> 节点3,权值为1 ,minDist[5] 还是默认数值max,所以不能基于节点5去更新节点3,所以minDist数组不发生改变。
边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 (经过上面的计算minDist[2]已经不是默认值,而是 1),更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3

边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + (-3),更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2

边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2

边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5

以上就是对所有边进行了一次松弛之后的结果。
那么需要松弛几次才能得到起点(节点1)到终点(节点6)的最短距离呢。
这里我们需要一个结论:对所有边松弛一次,相当于计算起点到达与起点一条边相连的节点的最短距离。
上面的距离中,我们得到里起点达到与起点一条边相邻的节点2 和 节点3 的最短距离,分别是 minDist[2]和minDist[3]。但我们知道minDist[3] = 5并不是最短的距离,真正最短的距离应该是节点1 -> 节点2 -> 节点5 -> 节点3 这条路线距离是4,才是最短距离。
但我们需要注意的是对所有边松弛一次,相当于计算起点到达与起点一条边相连的节点的最短距离。这里说的是一条边相连的节点。
与起点(节点1)一条边相邻的节点,到达节点2最短距离是1,到达节点3 最短距离是5。而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线是与起点三条边相连的路线了。
那么我们可以发现所以对所有边松弛一次能得到与起点一条边相连的节点最短距离,对所有边松弛两次可以得到与起点两条边相连的节点的最短距离,
那对所有边松弛三次可以得到与起点三条边相连的节点的最短距离,这个时候,我们就能得到到达节点3真正的最短距离,也就是节点1 -> 节点2 -> 节点5 -> 节点3这条路线。
那么总的来说,节点数量为n的情况下,起点到终点,最多是n - 1条边相连(没有环)那么无论图是什么样的,边是什么样的顺序,我们对所有边松弛n-1次就一定能得到起点到达终点的最短距离。
其实也同时计算出了,起点到达所有节点的最短距离,因为所有节点与起点连接的边数最多也就是 n-1条边。
这就是Bellman_ford的核心算法思路,主要就是两个关键点:“松弛”究竟是个啥?为什么要对所有边松弛 n - 1 次 (n为节点个数)?
代码:最后可以写出代码
//时间复杂度: O(N * E) , N为节点数量,E为图中边的数量
//空间复杂度: O(N) ,即 minDist 数组所开辟的空间
#include <iostream>
#include <vector>
#include <list>
#include <climits>
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
for (vector<int> &side : grid) { // 每一次松弛,都是对所有边进行松弛
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
minDist[to] = minDist[from] + price;
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
return 0;
}Bellman_ford总结
Bellman_ford算法,是用于解决存在负权值的最短路径算法,其蒜贩的核心思路是对所有边进行n-1 次松弛,要弄明白什么是”松弛“,为何要进行n - 1次松弛。
总结
今天主要是讲解了dijkstra算法的优化版本,通过堆进行优化,主要从边的角度出发,适用于稀疏图,时间复杂度会更低。
接着讲解了解决图中存在负权值的情况的Bellman_ford算法,关键是理解松弛的概念,和理解为什么n-1次松弛,每次松弛都相当于计算起点到达与起点一条边相连的节点的最短距离。