度量最小距离
对于 K-means 聚类算法而言,找到质心是一项既核心又重要的任务,找到质心才可以划分出距离质心最近样本点。从数学角度来讲就是让簇内样本点到达各自质心的距离总和最小。
通过数学定义,我们将“质心”具象化,既然要使“距离的总和最小”,那么第一步就是确定如何度量距离,K-means 算法通过『欧几里得距离』来衡量质心与样本点之间的距离。前面在学习 KNN 算法时,我们介绍了『闵可夫斯基距离』,其公式如下:
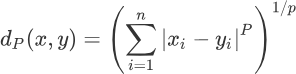
上述式子中 "∑" 符号称为求和符号,与 sum 函数功能一致,闵氏距离是一组代数形式的公式,通过给 P 设定不同的值,就能用闵氏距离得到不同的距离表达式。当 P =1 时,可以得到曼哈顿街区距离(简称“曼哈顿距离”);P = 2 时即可得到欧几里得距离,该公式常用于度量两点之间的直线距离,表达式和 L2 范式相同,如下所示:
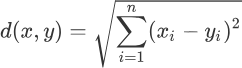
举个简单的例子:如果第 j 个簇内有若干个数据点(比如 m 个),根据上述欧几里得距离公式就可以计算出簇中各个点到质心z的距离总和,如下所示:
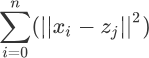
注意,上述公式中的 zj 是簇内所有样本点求均值的结果。
我们知道 K-measn 算法中会有 K 个簇,因此就要使每个簇内的数据点到质心的距离都可以达到最小,最终使得距离的总和最小。您可以这样理解,K 个簇共同组成了一个集合(这里定义为 A 集合),在 A 集合中每个簇的样本点到各自质心的距离都是最小的,因此可得如下表达式:
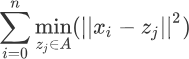
总结
上述内容,从数学的角度对 K-means 算法的原理进行了深入剖析,下面我们对 K-means 算法的流程进行回顾,可分以下四步:
- 随机选取 K 个对象,并以它们为质心;
- 计算数据集样本点到质心的距离;
- 根据样本点距离质心的距离将其分簇(类),距离哪个近,划分到哪个簇(类);
- 以簇内所有样本点的均值重新计算质心,,然后重复第二步,直到划分的簇(类)不在变化后停止。
K-means 算法是属于无监督学习算法,常用于解决聚类问题,通过给算法模型输入一个包含多种特征信息的样本点,会返回一个相应的类别编号(或称簇别),从而完成样本数据点的类别划分。
注意,判定聚类任务完成的终止条件并不是唯一的,常用方法有三个:
- 簇内数据点向质心靠拢、收敛,使得质心点不再发生明显的变化;
- 使用误差平方和(即 SSE)来衡量,当误差平和的值越小时,表示数据点越接近于他们的质心,聚类效果越好;
- 设定指定的定迭代次数,即最多选取几次质心点,不过这种方法,未必能达到最好的分类效果。