图+代码 | Bloom Filter实现及应用

什么是布隆过滤器（Bloom Filter）？

布隆过滤器是一种空间复杂度很低的概率型数据结构，用于判断一个元素是否在一个集合中。它有两种可能的返回结果：

元素可能在集合中：这可能是一个真阳性（确实在集合中）或假阳性（实际上不在集合中）。
元素肯定不在集合中：这是一个真阴性。

简单来说，布隆过滤器能告诉你一个元素可能存在或肯定不存在。它非常节省内存，但有一定概率会给出错误的“存在”结果（即假阳性）。

布隆过滤器是如何工作的？

假设我们要比较两个字符串是否相同，我们不会存储整个字符串，而是计算出这些字符串的哈希值，然后比较哈希值即可，如果两个哈希值不相等，可以肯定这2个字符串不相同，否则这两个字符串可能相同。

但是，有一个问题：哈希函数的值域是有限的，比如它可能只能生成 0 到 999 之间的数值。这意味着不同的字符串可能会生成相同的哈希值，这种情况叫做哈希冲突。因此，仅仅依赖一个哈希值来判断字符串相等是有风险的。

为了降低这种冲突带来的风险，我们可以使用多个哈希函数。即对同一个字符串使用不同的哈希函数，得到多个哈希值。如果两个字符串的所有哈希值都相同，那么它们很有可能相等；如果其中任何一个哈希值不同，我们就可以确定字符串不同。

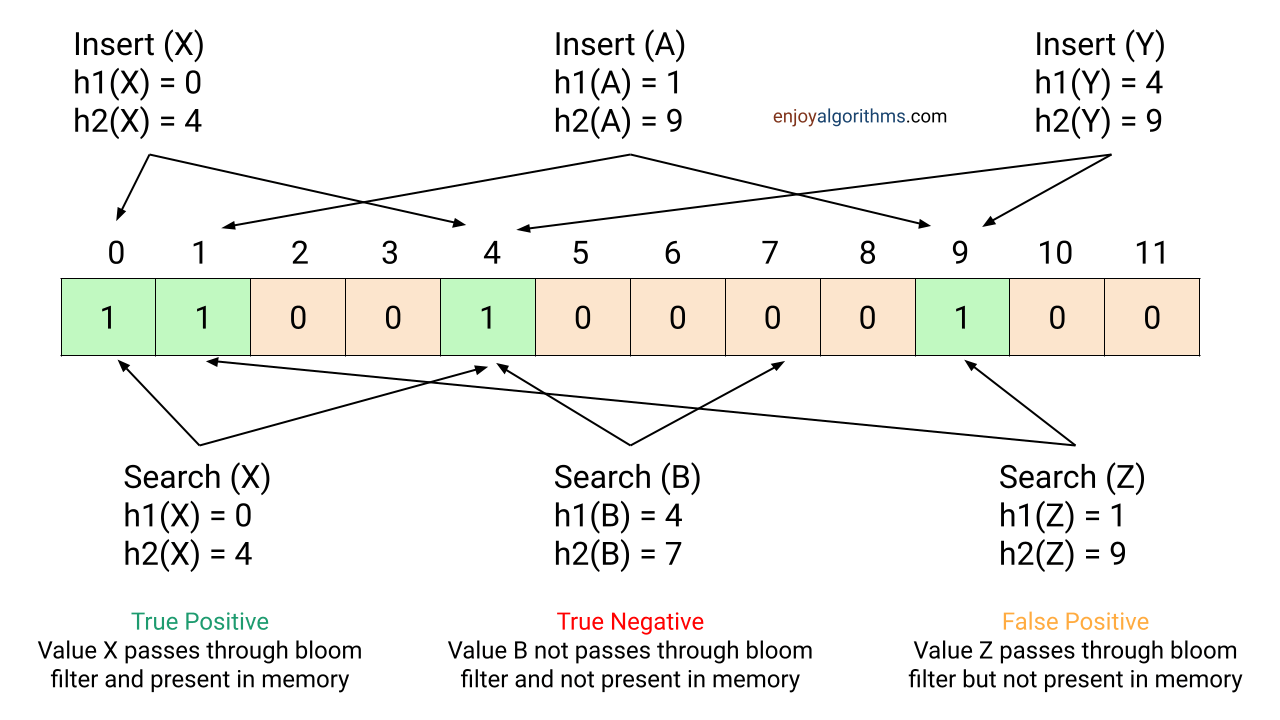
布隆过滤器是一种使用多个哈希函数的具体应用，它用来判断一个元素是否在一个集合中。

布隆过滤器是一个只包含 0 和 1 的位数组，每个位置代表一个比特（bit）。当你插入一个元素时，你用多个哈希函数计算它们的位置，并将位数组这些位置上的比特设置为 1。如果你想检查一个元素是否在集合中，同样对待检查元素用多个哈希函数计算它们的位置，然后只需检查位数组这些位置是否全都是 1。只要有一个位置是 0，那么这个元素一定不在集合中。

将元素插入到布隆过滤器

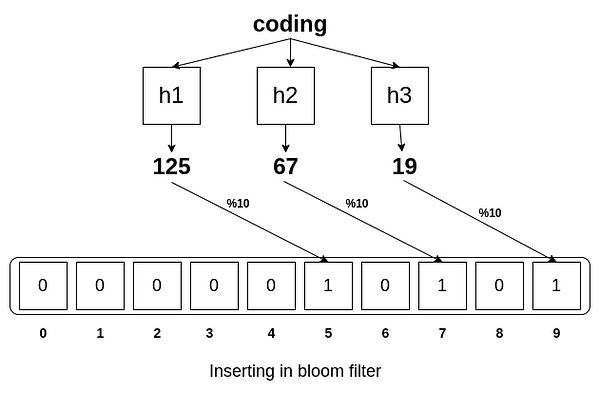
假设我们要将字符串 “coding” 插入布隆过滤器。首先，我们使用多个哈希函数对这个字符串进行哈希运算，得到不同的哈希值。例如，我们这里使用三个不同的哈希函数：

h1(“coding”) = 125
h2(“coding”) = 67
h3(“coding”) = 19

现在，我们假设布隆过滤器的大小是 10，即我们有一个长度为 10 的位数组。我们需要将哈希值对 10 取模以确保索引在布隆过滤器的位数组范围 0 到 9 之间：

125 % 10 = 5
67 % 10 = 7
19 % 10 = 9
于是，我们在位数组的索引 5、7 和 9 处设为1。

同样，我们可以将"music"这个字符串也添加到布隆过滤器中：

h1(“music”) = 290
h2(“music”) = 145
h3(“music”) = 2

对 10 取模:

290 % 10 = 0
145 % 10 = 5
2 % 10 = 2

添加了2个字符串的布隆过滤器如下：

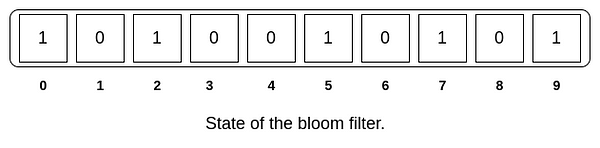
其中，索引为5的位置为 1 是这两个单词都做了贡献。

查询一个元素是否存在

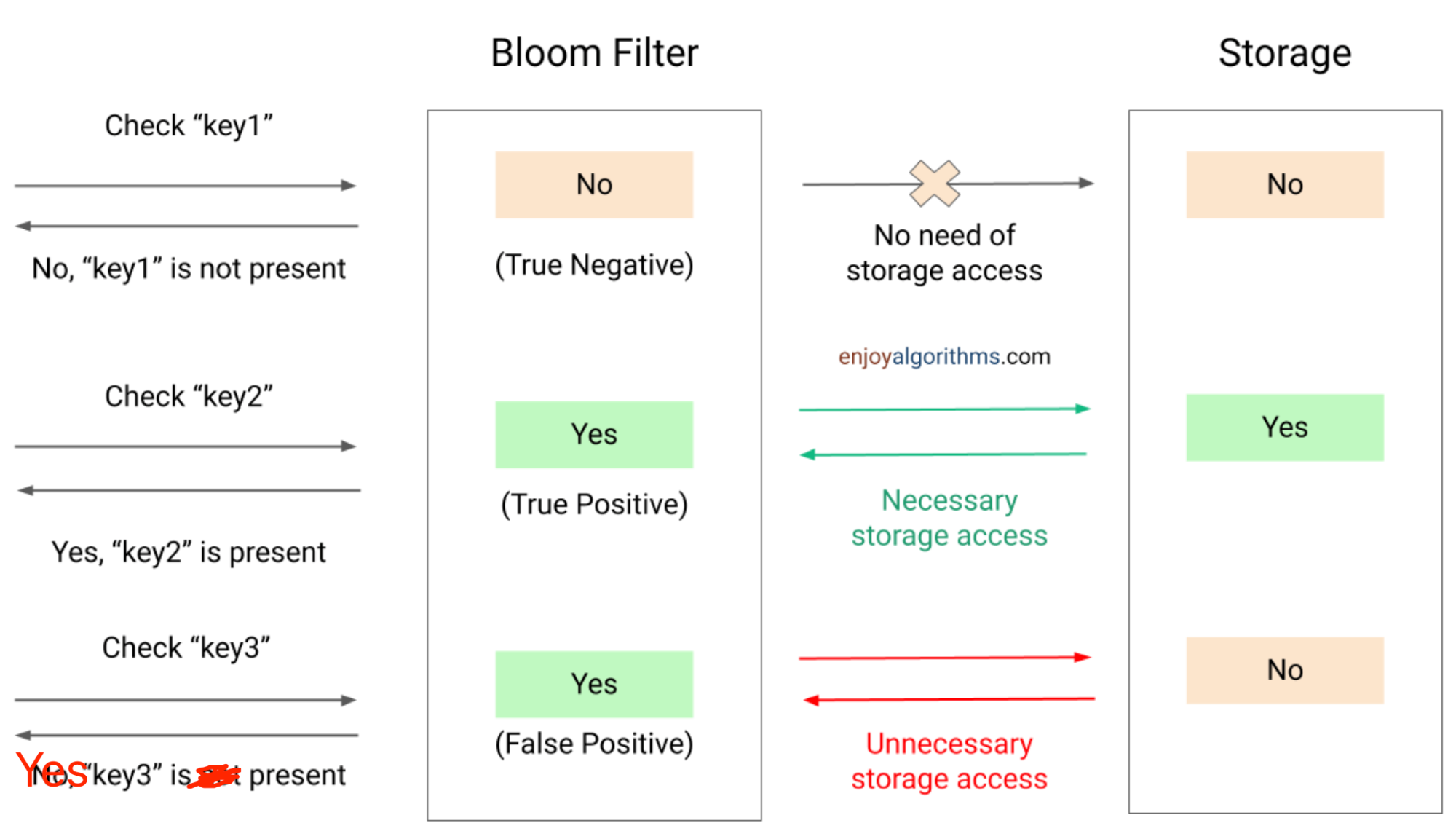
如果我们想查询一个元素是否存在于布隆过滤器中，我们将待查询的元素使用相同的哈希函数然后对位数组大小求模，然后判断对应位数组的索引位是否都设置为1，如果都为1，则该元素可能存在布隆过滤器中，只要有一个索引位为0，我们就能肯定该元素不存在布隆过滤器中。

100%不存在的案例

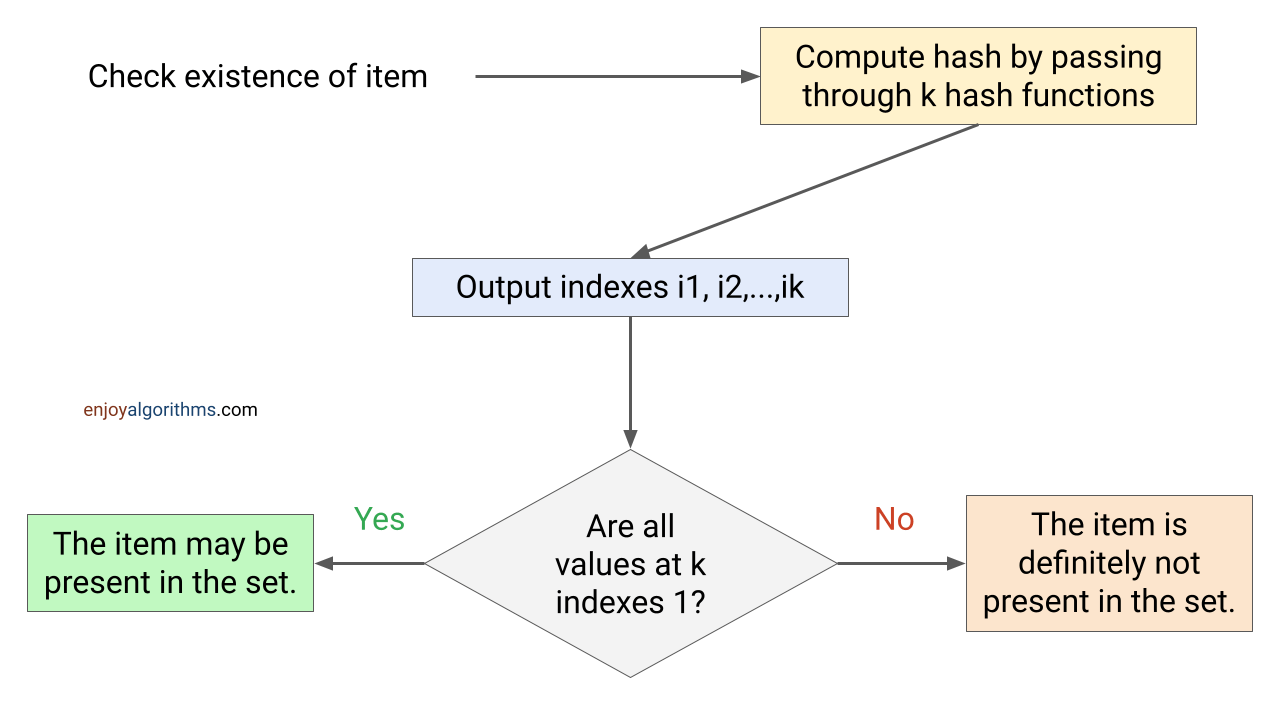
现在假设我们想查询 “cat” 是否在布隆过滤器中。我们同样使用相同的哈希函数对"cat"进行哈希运算，得到：

h1(“cat”) = 233 % 10 = 3
h2(“cat”) = 155 % 10 = 5
h3(“cat”) = 9 % 10 = 9

然后，我们检查位数组索引 3、5 和 9。如果这些索引中的所有位都为1，则表示 “cat” 可能存在。但如果其中任何一位是0，那么我们可以确定 “cat” 不在集合中。

我们可以看到，尽管位数组索引5和9的位为1，但是索引3处是0，因此我们可以100%肯定"cat"不在集合中。

可能存在的案例

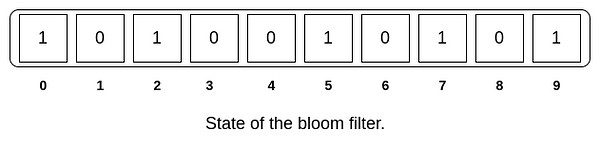
现在假设我们想查看"gaming"是否存在，我们将“gaming”这个元素通过相同的哈希函数（h1、h2、h3）得到了以下结果：

h1(“gaming”) = 235 % 10 = 5
h2(“gaming”) = 60 % 10 = 0
h3(“gaming”) = 22 % 10 = 2

然后，我们检查位数组处索引 0、2 和 5是否都被设置为1。我们看到这些索引都已经被设置为1。然而，我们知道“gaming”实际上并不在集合中，所以这是一个误报（False Positive）。

如何预测误报的概率？

我们可以通过数学公式来预测误报的概率。以下是一些符号的定义：

n：插入到Bloom过滤器中的元素数量。
m：Bloom过滤器的长度（位数组的大小）。
k：哈希函数的数量。

可以看出，当m趋向于无穷大时，误报率趋向于零。另一种减少误报率的方法是使用多个哈希函数。

布隆过滤器的实现示例

以下是一个简单的 Python 实现：

import mmh3  # MurmurHash 3，常用于布隆过滤器
import math

class BloomFilter:
    def __init__(self, m, k):
        self.m = m  # 布隆过滤器的大小（位数组的长度）
        self.k = k  # 哈希函数的数量
        self.n = 0  # 插入的元素数量
        self.bloomFilter = [0] * self.m  # 初始化位数组为0
        
    def getBitArrayIndices(self, item):
        """
        计算 item 的哈希值并返回需要设置的位数组索引列表
        """
        indexList = []
        for i in range(1, self.k + 1):
            indexList.append((hash(item) + i * mmh3.hash(item)) % self.m)
        return indexList
        
    def add(self, item):
        """
        插入一个元素到布隆过滤器
        """
        for i in self.getBitArrayIndices(item):
            self.bloomFilter[i] = 1
        self.n += 1
    
    def contains(self, key):
        """
        检查元素是否在布隆过滤器中
        """
        for i in self.getBitArrayIndices(key):
            if self.bloomFilter[i] != 1:
                return False
        return True
        
    def generateStats(self):
        """
        计算布隆过滤器的统计信息，比如错误率
        """
        n = float(self.n)
        m = float(self.m)
        k = float(self.k)
        probability_fp = math.pow((1.0 - math.exp(-(k*n)/m)), k)

        print("元素数量: ", n)
        print("布隆过滤器大小: ", m)
        print("哈希函数数量: ", k)
        print("假阳性概率: ", probability_fp)
        print("假阳性率: ", probability_fp * 100.0, "%")

对应的 Java代码如下：

import java.util.BitSet;
import java.util.Random;

public class BloomFilter {

    private int m;  // Bloom filter 的大小
    private int k;  // 哈希函数的数量
    private int n;  // 插入的元素数量
    private BitSet bloomFilter;
    private Random[] hashFunctions;

    public BloomFilter(int m, int k) {
        this.m = m;
        this.k = k;
        this.n = 0;
        this.bloomFilter = new BitSet(m);
        this.hashFunctions = new Random[k];
        for (int i = 0; i < k; i++) {
            this.hashFunctions[i] = new Random(i);
        }
    }

    private int[] getBitArrayIndices(String item) {
        int[] indexList = new int[k];
        for (int i = 0; i < k; i++) {
            indexList[i] = Math.abs(hashFunctions[i].nextInt(item.hashCode())) % m;
        }
        return indexList;
    }

    public void add(String item) {
        int[] indices = getBitArrayIndices(item);
        for (int index : indices) {
            bloomFilter.set(index);
        }
        n++;
    }

    public boolean contains(String key) {
        int[] indices = getBitArrayIndices(key);
        for (int index : indices) {
            if (!bloomFilter.get(index)) {
                return false;
            }
        }
        return true;
    }

    public int length() {
        return n;
    }

    public void generateStats() {
        double n = (double) this.n;
        double m = (double) this.m;
        double k = (double) this.k;
        double probability_fp = Math.pow((1.0 - Math.exp(-(k * n) / m)), k);

        System.out.println("Number of elements entered in filter: " + n);
        System.out.println("Number of bits in filter: " + m);
        System.out.println("Number of hash functions used: " + k);
        System.out.println("Predicted Probability of false positives: " + probability_fp);
        System.out.println("Predicted false positive rate: " + (probability_fp * 100.0) + "%");
    }

    public void reset() {
        this.n = 0;
        this.bloomFilter.clear();
    }

    public static void main(String[] args) {
        BloomFilter bloomFilter = new BloomFilter(10, 3);
        bloomFilter.add("coding");
        bloomFilter.add("music");
        System.out.println(bloomFilter.contains("gaming")); // 输出 false（有可能是误报）
        bloomFilter.generateStats();
    }
}