信号处理——自相关和互相关分析

news2024/9/29 7:16:38

1.概括

在信号处理中，自相关和互相关是相关分析非常重要的概念，它们能分析一个信号或两个信号在时间维度的相似性，在振动测试分析、雷达测距和声发射探伤得到了广泛的应用。自相关分析的研究对象为一个信号，互相关分析的研究对象为两个信号。

本文以互相关分析为例，流程如下图所示，构建了一个余弦信号，并人为设置滞后延迟20个采样点（准确来说是采样间隔），构建了另一个余弦信号，通过计算了两个余弦信号的互相关函数，分析了两个信号的相似性，找到了两个信号之间的时间延迟，在工程实际中常用于进行故障源定位。此外，对比matlab的互相关函数xcorr，本文也采用手动计算的方法，计算了互相关函数，验证了本文手工计算方法的准确性。

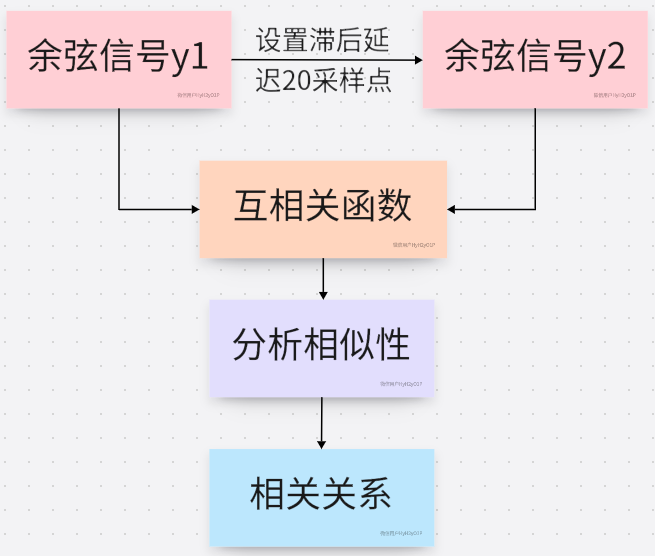
关于自相关、互相关以及相关系数的更多公式定义和讲解，请参考链接：

相关系数、自相关、互相关等概念理解：https://zhuanlan.zhihu.com/p/613949451

该内容参考了一些资料：

1、书籍：机械工程测试技术基础第3版熊诗波编著

2、相关系数、自相关、互相关等概念理解：https://zhuanlan.zhihu.com/p/613949451

3、matlab官网的函数解释：

https://ww2.mathworks.cn/help/matlab/ref/xcorr.html?searchHighlight=xcorr&s_tid=srchtitle_support_results_1_xcorr

代码采用了Matlab 2024a进行运行，欢迎大家测试和提出问题！

2.具体案例

互相关分析是分析信号间时间前后相似的重要手段，它在故障源定位中得到了广泛的应用。本文分析的仿真信号如下图所示：

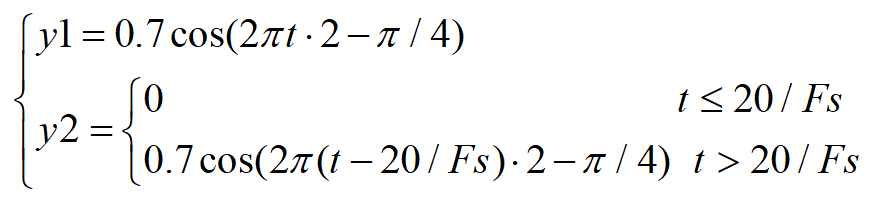
这里，y1为原始的余弦信号，y2为延迟了20个采样点（准确来说是采样间隔）的余弦信号，采样频率为100，信号长度为100，即采集时间为1s，获得时域波形如下图所示：

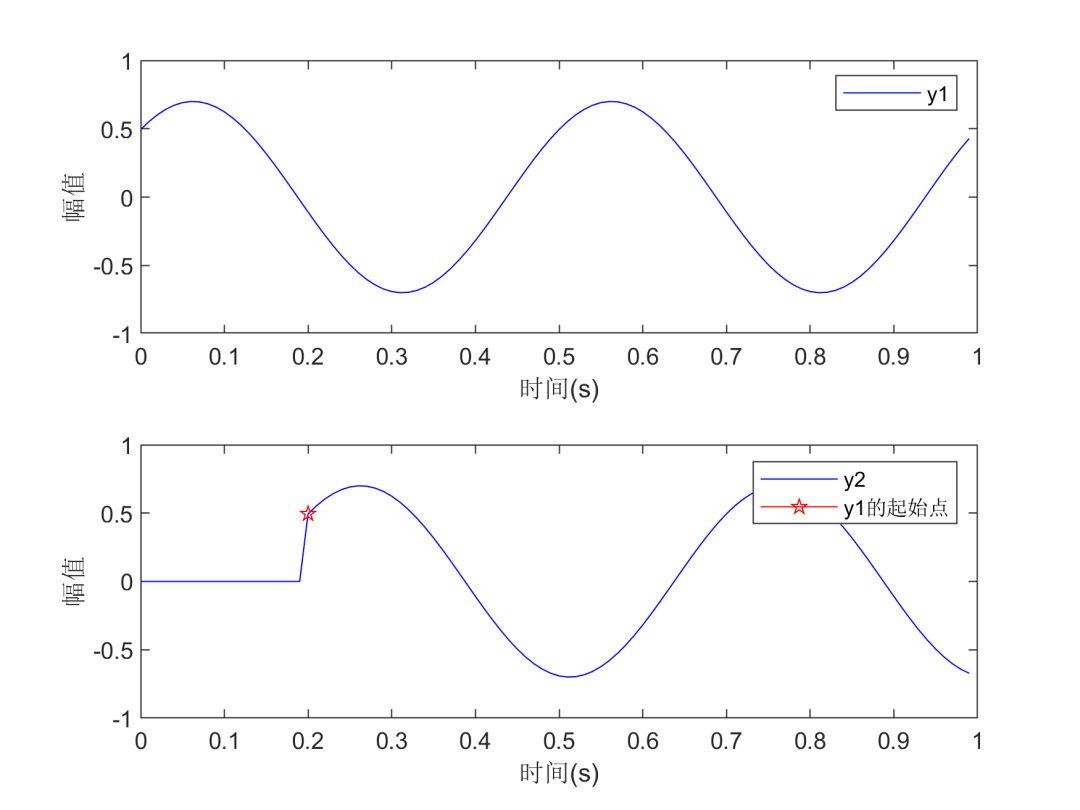
从上图中，能明显发现y2相对于y1延迟了差不多0.2s（一个采样间隔是1/100=0.01s,20个就是0.20s）。采用matlab的互相关计算函数xcorr函数，获得互相关函数如下图所示：

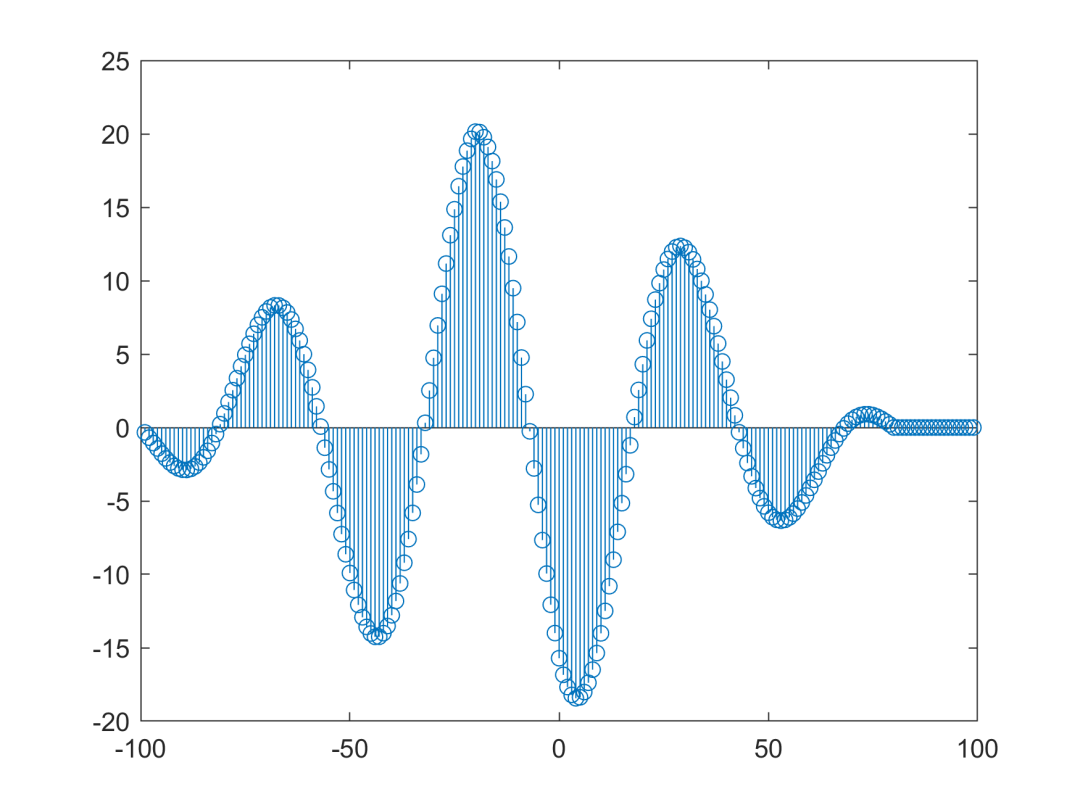
上图为一个相关函数的茎叶图，用的stem函数。从上图中能发现，存在正相关和负相关的最大点，表明了不同延迟或超前时两个信号的相关性最强。关于具体意义稍后讨论哈！下图为手动计算互相关函数和matlab的xcorr函数的结果对比图：

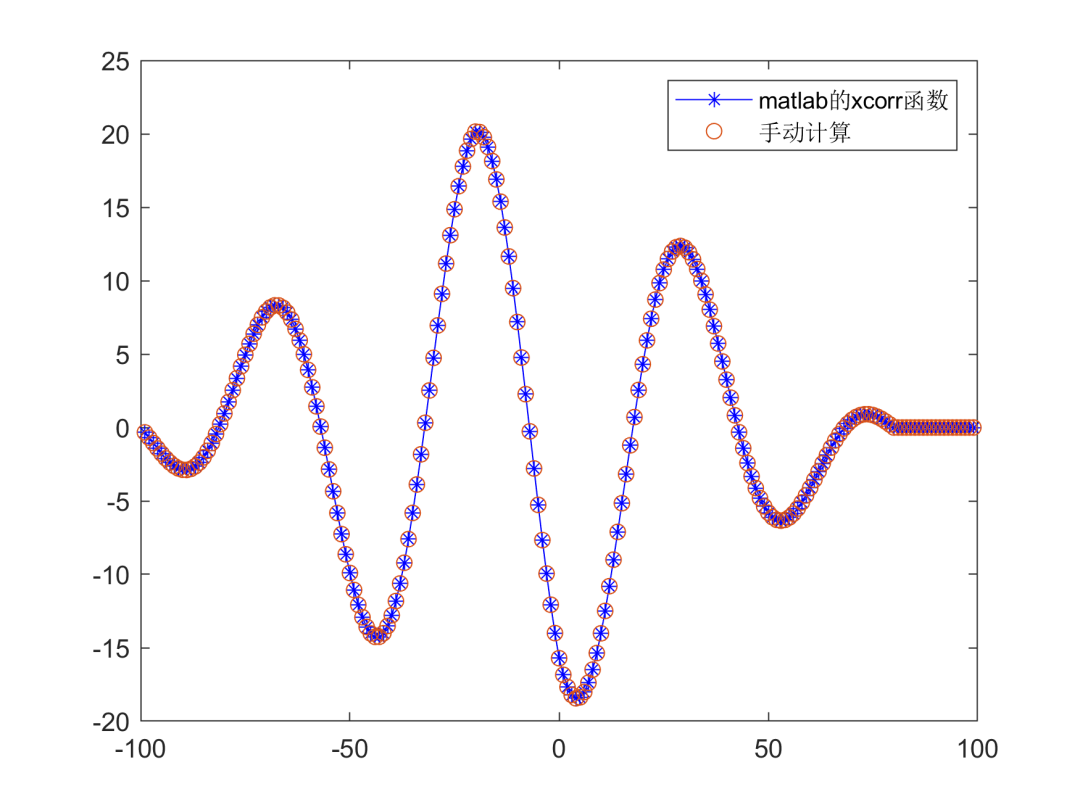
从上图中能定性地发现，手动计算结果基本和matlab的结果保持一致。同时，定量计算的平均偏差（平均偏差为两数差的绝对值的平均数）结果如下，二者的偏差为0。

综上分析，手动计算的互相关函数是正确的！关于互相关函数的计算方式，请参考链接：相关系数、自相关、互相关等概念理解：https://zhuanlan.zhihu.com/p/613949451。这里就不给大家展开了。

紧接互相关函数结果进行分析。如下图所示

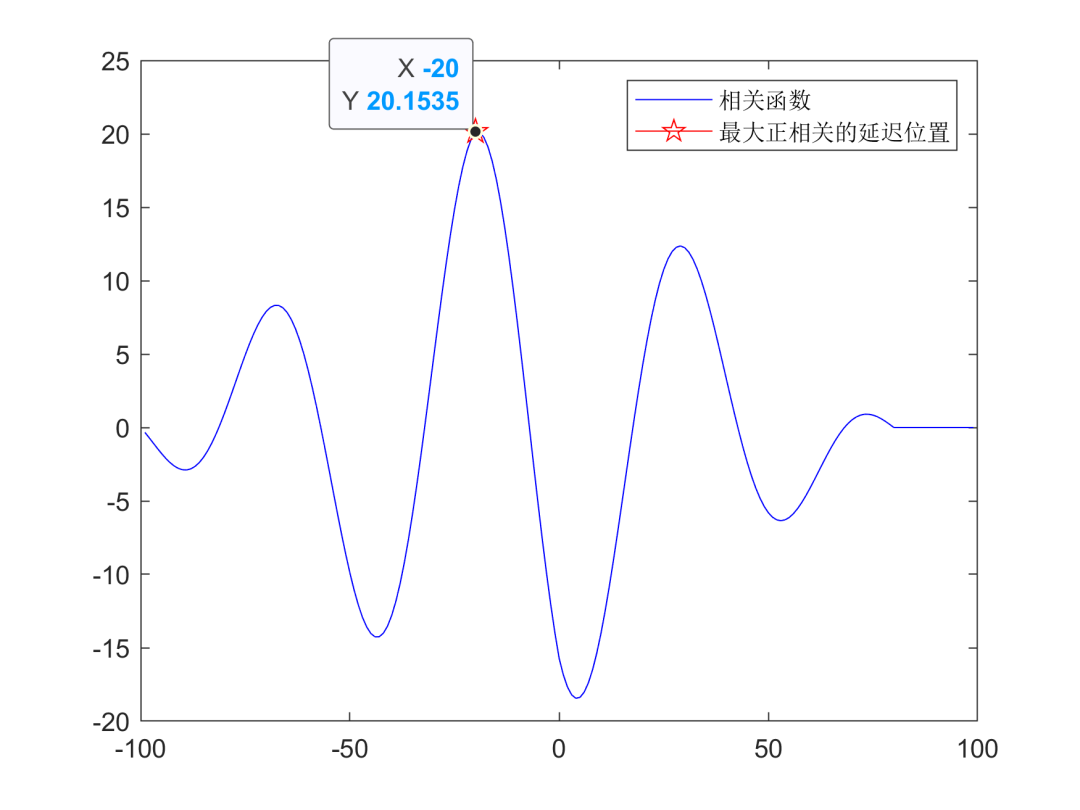
以最大正相关的点为例，发现互相关函数最大的峰值点（-20，20.1535），20表示使两个信号之间的相关程度最大的时间间隔是20，负号表示超前还是滞后，我用的matlab的xcorr函数，代码具体为[c,lags] = xcorr(y1,y2)，c为互相关函数的y轴，lags为互相关函数的x轴。因此可以断定，-20的意思为y2比y1滞后20个采样间隔。相反，如果是正号的意思就是超前，大家可以自行验证，欢迎大家指出错误哈！此外，通过分析手动计算互相关函数过程也能发现，负号的意思为滞后。代码后续增加了一个if判断函数，来自动分析互相关函数结果，结果如上上图所示。

综上分析，互相关函数分析结果与信号人为设置结果相一致，验证了本案例的正确性！

3.具体代码

代码主要有一个：

1、main.m（主函数，用于互相关函数分析）

2、matlab中计算互相关函数为xcorr，更多使用细节参考https://ww2.mathworks.cn/help/matlab/ref/xcorr.html?searchHighlight=xcorr&s_tid=srchtitle_support_results_1_xcorr

%% 信号的自相关和互相关分析
%% 作者：冷漠
%% 时间：2024年7月29日
%% 关注公众号 ："故障诊断与寿命预测工具箱",每天进步一点点
clc
clear all
close all
%%

fs=100;                                             %采样频率
L=100;                                              %信号长度
t=(0:L-1)/fs;                                          %时间序列
y1=0.7*cos(2*pi*2*t-pi/4);    %信号y1
y2=circshift(y1,20);
y2(1:20)=0;

%画图
figure;
subplot(211);plot(t,y1,'b-');xlabel('时间(s)');ylabel('幅值');
legend('y1');
subplot(212);plot(t,y2,'b-');xlabel('时间(s)');ylabel('幅值');hold on;
plot(t(21),y2(21),'Color','r','Marker','pentagram');
legend('y2','y1的起始点')

%计算互相关
[c,lags] = xcorr(y1,y2);
figure;
stem(lags,c)

%手动计算互相关
y11=zeros(3*length(y1)-2,1);
y22=zeros(3*length(y2)-2,1);
y11(length(y1):2*length(y1)-1)=y1;
y22(1:length(y2))=y2;

for i=1:2*length(y1)-1
    c1(i)=sum(y11.*y22);
    y22=circshift(y22,1);
end

%matlab函数和手动计算函数之间对比分析
figure;
plot(lags,c,'b-*');hold on;
plot(lags,c1,'o');
legend('matlab的xcorr函数','手动计算')

fprintf('matlab的xcorr函数获得相关函数与手动计算之间的差为%f \n',sum(abs(c1-c))/length(c1));

%分析结果
[c_max,index]=max(c);
%相关函数
figure;plot(lags,c,'b-');hold on;
plot(lags(index),c_max,'Color','r','Marker','pentagram','MarkerSize',10);
legend('相关函数','最大正相关的延迟位置')

%信号的对应关系
figure;
subplot(211);plot(t,y1,'b-');xlabel('时间(s)');ylabel('幅值');
legend('y1');
subplot(212);plot(t,y2,'b-');xlabel('时间(s)');ylabel('幅值');hold on;
plot(t(abs(lags(index))+1),y2(abs(lags(index))+1),'Color','r','Marker','pentagram');
legend('y2','y1的起始点')

%输出分析结果
if lags(index)<0
    fprintf('y2比y1滞后%d 个采样点 \n',abs(lags(index)));
else
    fprintf('y2比y1超前%d 个采样点 \n',abs(lags(index)));
end

4.细节说明

1.xcorr是matlab的自相关和互相关的函数，挺方便的，推荐大家使用，自相关函数只有一个输入，请大家参考官方使用介绍。互相关分析代码为：[c,lags] = xcorr(y1,y2)，c为互相关函数的y轴，lags为互相关函数的x轴，c的结果中，如果最大峰值的横坐标(即lags(max(c)))为-20，则表示y2比y1滞后了20个采样间隔（y1比y2超前了20个采样间隔），如果为20，则表示y2比y1超前了20个采样间隔（y1比y2滞后了20个采样间隔）。

2.关于互相关函数、自相关函数的具体公式定义和计算方法可以参考如下链接：

相关系数、自相关、互相关等概念理解：https://zhuanlan.zhihu.com/p/613949451