【Python机器学习】支持向量机——在复杂数据上应用核函数

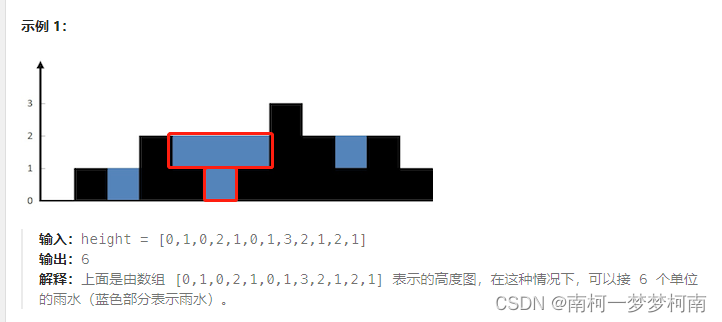
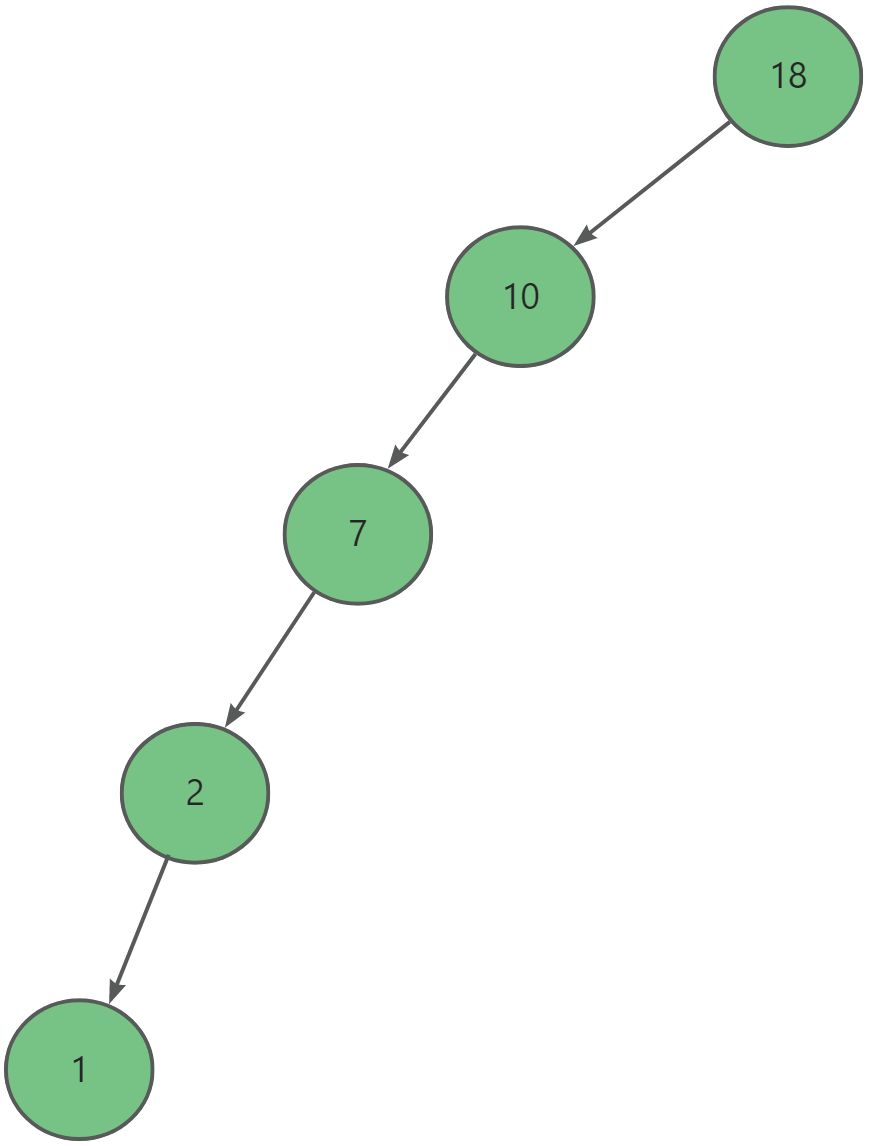
上图中，数据中存在某种可以识别的模式，其中一个问题就是：我们能否想线性情况一样，利用强大的工具来捕捉数据中的这种模式？

利用核函数将数据映射到高维空间

在上图中，数据点处于一个圆中，人类的大脑能够意识到这一点，但是对于分类器而言，它只能识别分类器的结果是大于0还是小于0。如果只在x和y轴构成的坐标系中插入直线进行分类的话，我们并不会得到理想的结果。我们或许可以对园中的数据进行某种形式的转换，从而得到某些新的变量来表示数据。在这种情况下，我们就更容易得到大于0或者小于0的测试结果。在这个例子中，我们将数据从一个特征空间转换到另一个特征空间。在新空间下，我们可以很容易利用已有的工具对数据进行处理。数学家们喜欢将这一过程称之为从一个特征空间到另一个特征空间的映射。通常情况下，这种映射会降低维特征空间映射到高维空间。

这种从某个特征空间到另一个特征空间的映射是通过核函数来实现的。我们可以把核函数想象成一个包装器或者是接口，它能把数据从某个很难处理的形式转换成另一个比较容易处理的形式。距离计算的方法有很多种，经过空间转换之后，我们可以从高维空间中解决线性问题，这也就等价于在低维空间解决非线性问题。

SVM优化中一个特别好的地方就是：所有的运算都可以写成内积（点积）的形式。向量的内积指的是两个向量相乘，之后得到单个标量或者数值。我们可以把内积运算替换成核函数，而不必做简化处理。将内积替换成核函数的方式被称为核技巧或者核“变电”。

核函数并不仅仅应用于支持向量机，很多其他的机器学习算法也都用到核函数。

径向基核函数

径向基函数是SVM中常用的一个核函数。径向基函数是一个采用向量作为自变量的函数，能够基于向量距离运算输出一个标量。这个距离可以是从<0,0>向量或者其他向量开始计算的距离。

径向基函数的高斯版本的具体公式为：

$k(x,y)=exp\left ( \frac{-\left \| x-y \right \|^{2}}{2\sigma ^{2}} \right )$

其中， $\sigma$ 是用户定义的用于确定达到率或者说函数值跌落到0的速度参数。

上述高斯核函数将数据从其特征空间映射到更高维的空间，具体来说这里是映射到一个无穷维的空间。高斯核函数只是一个常用的核函数，使用者并不需要确切地理解数据到底是如何表现的，而且使用高斯核函数还会得到一个理想的结果。上面的例子中，数据点基本都在一个圆内。对于这个例子，我们可以直接检查原始数据，并意识到只要度量数据点到圆心的距离即可。然而如果碰到了一个不是这种形式的新数据集，那么就会陷入困境。在该数据集上，使用高斯核函数可以得到恨到的记过，当然该函数也可以用于许多其他的数据集，并且也能得到低错误率的结果。

修改optStruct类：

def kernelTrans(X,A,kTup):
    m,n=shape[X]
    K=mat(zeros((m,1)))
    if kTup[0]=='lin':
        K=X*A.T
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow=X[j,:]-A
            K[j]=deltaRow*deltaRow.T
        K=exp(K/(-1*kTup[1]**2))
    else:
        raise NameError('Houston We Have a Problem That Kernel is not recognized')
    return K

class optStruct:
    def __init__(self,dataMatIn,classLabels,C,toler,kTup):
        self.X=dataMatIn
        self.labelMat=classLabels
        self.C=C
        self.tol=toler
        self.m=shape(dataMatIn)[0]
        self.alphas=mat(zeros((self.m,1)))
        self.b=0
        #误差缓存
        self.eCache=mat(zeros((self.m,2)))
        self.K=mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup)

kTup是一个包含核函数信息的元素。在初始化方法结束时，矩阵K先被构建，然后再通过调用函数kernelTrans()进行填充。全局的K值只需计算一次。然后，当想要使用核函数时，就可以对它进行调用。这些省去了很多冗余的计算开销。

当计算矩阵K时，该过程多次调用了kernelTrans()。该函数有3个输入参数：2个数值型变量和1个元组。元组kTup给出的是核函数的信息。元组的第一个参数是描述所用核函数类型的第一个字符串，其他2个参数都是核函数可能需要的可选参数。该函数首先构建出了一个列向量，然后检查元组以确定核函数的类型。这里只给出了2中类型，但是依然可以很容易地通过添加elif语句来扩展到更多选项。

在线性核函数的情况下，内积计算在“所有数据集”和“数据集中的一行”这两个输入之间展开。在径向基核函数的情况下，在for循环中对于矩阵的每个元素计算高斯函数的值。而在for循环结束之后，我们将计算过程应用到整个向量上去。值得一提的是，在NumPy矩阵中，除法符号意味着对矩阵元素展开计算而不像在MATLAB中一样计算矩阵的逆。

最后，如果遇到一个无法识别的元组，程序就会抛出异常，因为在这种情况下不希望程序再继续运行，这一点非常重要。

修改innerL()函数和calcEK()函数：


def innerL(i,oS):
    Ei=calcEk(oS,i)
    if ((oS.labelMat[i]*Ei<-oS.tol) and (oS.alphas[i]<oS.C)) or ((oS.labelMat[i]*Ei>oS.tol) and (oS.alphas[i]>0)):
        # 如果alpha可以更改，进入优化过程
        j,Ej=selectJ(i,oS,Ei)
        #随机选择第二个alpha
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        # 保证alpha在0与C之间
        if (oS.labelMat[i]!=oS.labelMat[j]):
            L=max(0,oS.alphas[j]-oS.alphas[i])
            H=min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])
        else:
            L=max(0,oS.alphas[j]+oS.alphas[i]-oS.C)
            H=min(oS.C,oS.alphas[j]+oS.alphas[i])
        if L==H:
            print('L==H')
            return 0
        # eta为最优修改量，如果eta=0，需要退出循环的当前迭代过程。
        eta=2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j]
        if eta>=0:
            print('eta>0')
            return 0
        oS.alphas[j]=oS.alphas[j]-oS.labelMat[j]*(Ei-Ej)/eta
        oS.alphas[j]=clipAlpha(oS.alphas[j],H,L)
        updateEk(oS,j)
        if (abs(oS.alphas[j]-alphaJold)<0.00001):
            print('j mot moving enough')
            return 0
        oS.alphas[i]=oS.alphas[i]+oS.labelMat[j]*oS.labelMat[i]*(alphaJold-oS.alphas[j])
        updateEk(oS,i)
        # 设置常数项
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,i] - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.K[i, j]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
                    oS.alphas[j] - alphaJold) * oS.K[j, j]
        if (0<oS.alphas[i]) and (oS.C>oS.alphas[i]):
            oS.b=b1
        elif (0<oS.alphas[j]) and (oS.C>oS.alphas[j]):
            oS.b=b2
        else:
            oS.b=(b1+b2)/2.0
        return 1
    else:
        return 0


def calcEk(oS,k):
    #对于给定的alpha值，计算E值并返回
    fXk=float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k]+oS.b)
    Ek=fXk-float(oS.labelMat[k])
    return Ek

在测试中使用核函数

下面：构造一个对文章开头数据进行有效分类的分类器，该分类器使用了径向基核函数。前面提到的径向基函数有一个用户定义的输入 $\sigma$ 。首先，我们需要确定它的大小，然后利用该核函数构建一个分类器。

代码实现：

def testRbf(k1=1.3):
    dataArr, labelArr = loadDataSet('testSetRBF.txt')
    # print(labelArr)
    b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000,('rbf',k1))
    dataMat=mat(dataArr)
    labelMat=mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=dataMat[svInd]
    labelSV=labelMat[svInd]
    print('there are %d Support Vectors' % shape(sVs)[0])
    m,n=shape(dataMat)
    errorCount=0
    for i in range(m):
        kernelEval=kernelTrans(sVs,dataMat[i,:],('rbf',k1))
        predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
        if sign(predict)!=sign(labelArr[i]):
            errorCount=errorCount+1
    print('错误率：',(float(errorCount)/m))
    dataArr,labelArr=loadDataSet('testSetRBF2.txt')
    errorCount=0
    dataMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    m, n = shape(dataMat)
    for i in range(m):
        kernelEval=kernelTrans(sVs,dataMat[i,:],('rbf',k1))
        predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
        if sign(predict)!=sign(labelArr[i]):
            errorCount=errorCount+1
    print('错误率：',(float(errorCount)/m))

函数中只有一个可选的参数，是高斯径向基函数中的一个用户定义变量。整个代码先从文件中读取数据集，然后在该数据集上运行platt SMO算法，其中核函数类型为rbf。

优化过程结束后，在后面的矩阵数学运算中建立了数据的矩阵副本，并且找出那些非零的alpha值，从而得到所需要的支持向量；同时，也就得到了这些支持向量和alpha的类别标签值。这些值仅仅是需要分类的值。

整个代码中最重要的是for循环最开始的两行，它们给出了如何利用核函数进行分类。首先利用结构化方法中使用过的kernelTrans()，得到转换后的数据。然后，再用其与前面的alpha及类别标签值求积。

运行结果：