无缝融入,即刻智能[2]:MaxKB内置强大工作流引擎,编排AI工作流程,满足多样化业务需求
1.简介
MaxKB(Max Knowledge Base)是一款基于 LLM 大语言模型的开源知识库问答系统,
-
官方网址:https://maxkb.cn/
-
GitHub:https://github.com/1Panel-dev/MaxKB
1.1 产品优势
- 开箱即用:支持直接上传文档、自动爬取在线文档,支持文本自动拆分、向量化、RAG(检索增强生成),智能问答交互体验好;
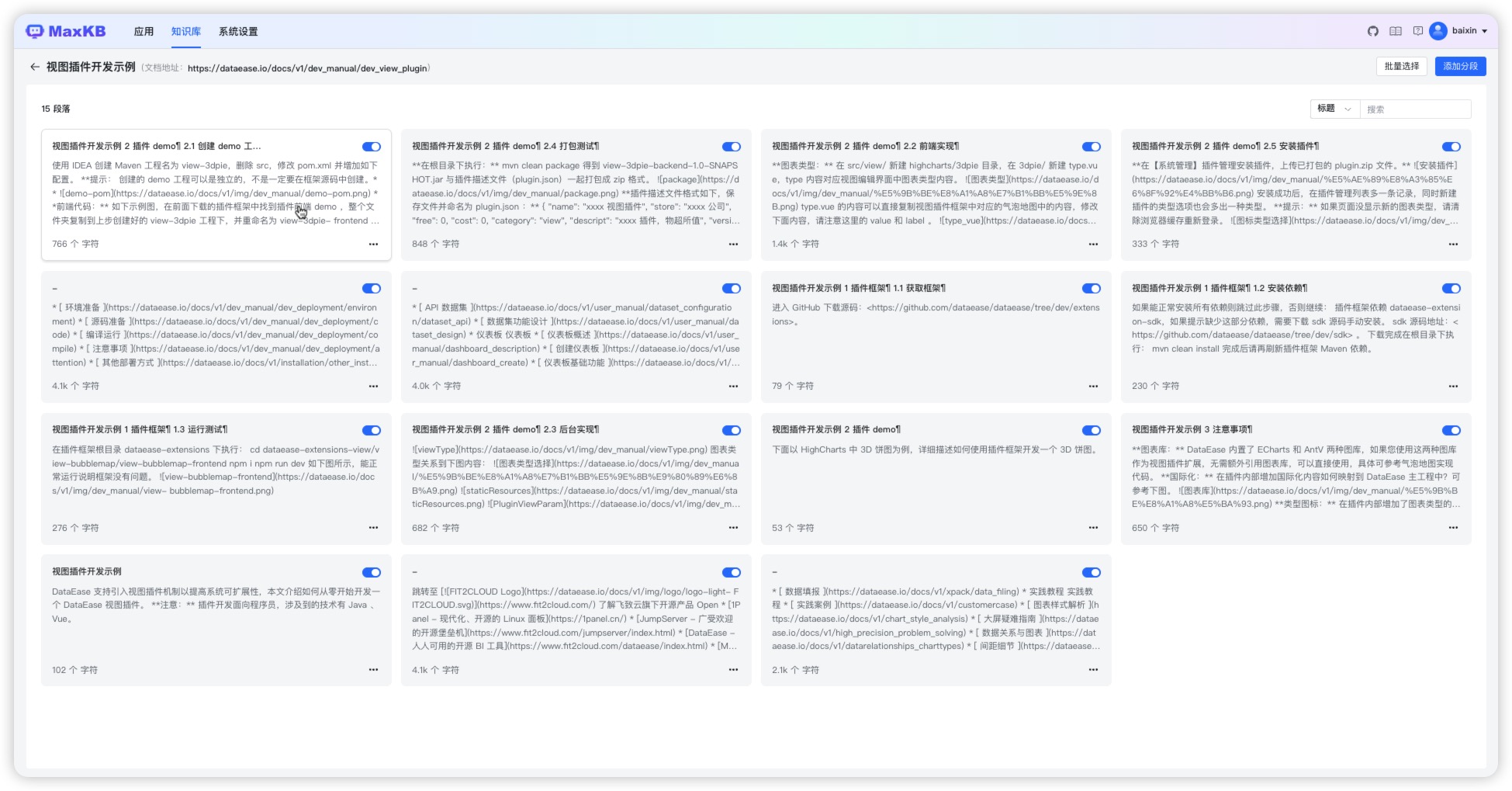
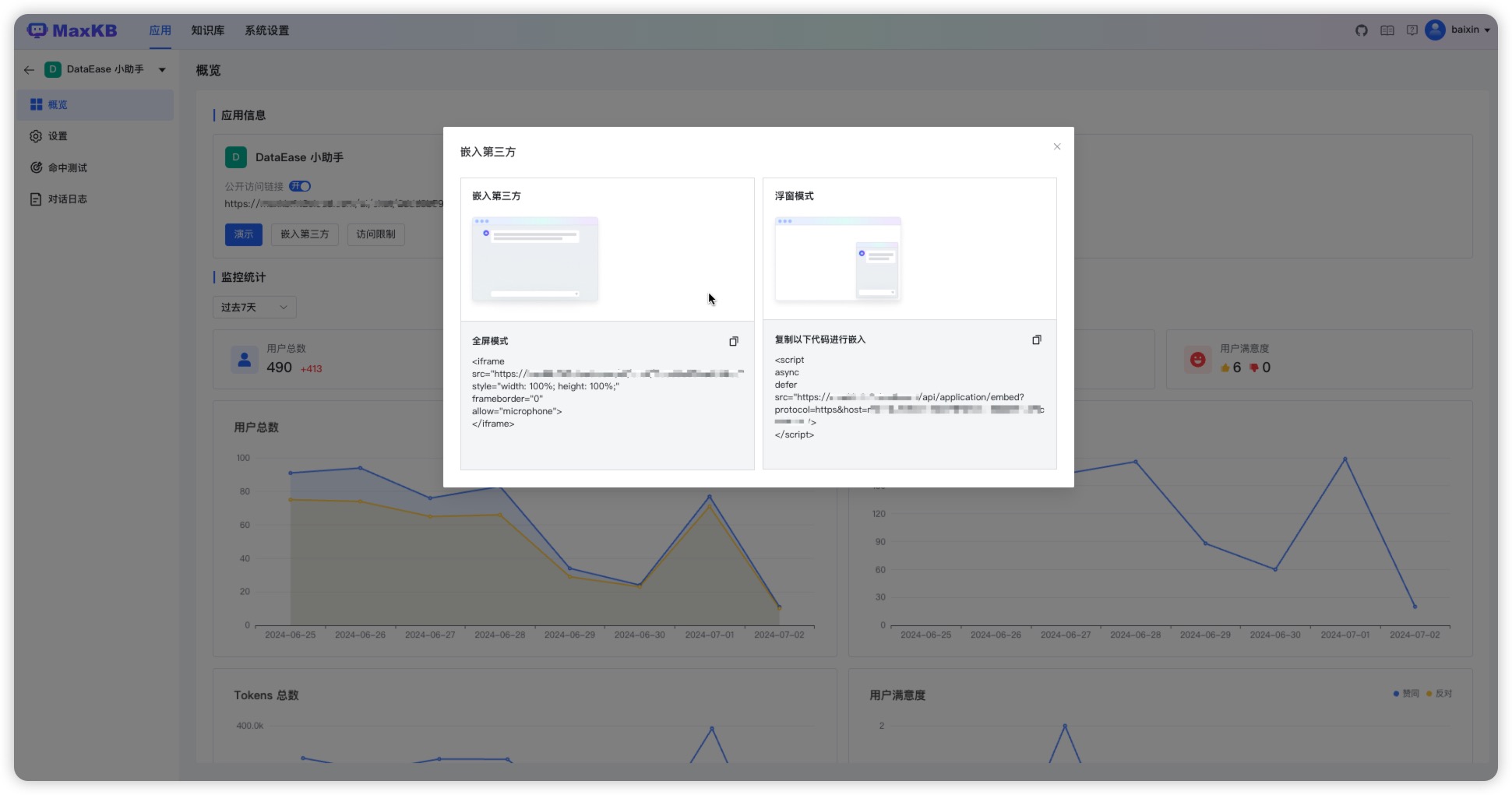
- 无缝嵌入:支持零编码快速嵌入到第三方业务系统,让已有系统快速拥有智能问答能力,提高用户满意度;
- 灵活编排:内置强大的工作流引擎,支持编排 AI 工作流程,满足复杂业务场景下的需求;