一 基础概念

广义线性模型（2）线性回归

【机器学习】一文看尽 Linear Regression 线性回归

二 步骤

使用sklearn中的库，一般使用线性回归器

• 首先，导入包： from sklearn.linear_model import LinearRegression
• 创建模型： linear =LinearRegression()
• 拟合模型： linear.fit(x,y)
• 模型的预测值： linear.predict(输入数据)
• 模型评估：计算 mean_squared_error 和 r2_score
• 线性回归模型的权重linear.coef_和偏置linear.intercept_

三 示例

3.1 单变量线性回归

1. 导入包

   # 导入包
   import matplotlib.pyplot as plt
   import numpy as np
   
   from sklearn import linear_model
   from sklearn.metrics import mean_squared_error, r2_score
   

2. 加载数据

   # 产生数据
   x = np.linspace(0,10,50) # 0到10等间隔产生50个数
   b = 1
   noise = np.random.uniform(-2, 2, size=50)
   y= 5*x + b + noise
   

3. 创建模型

   # 创建模型
   lr = linear_model.LinearRegression()
   

4. 模型预测

   # 模型训练
   lr.fit(np.reshape(x,(-1,1)),np.reshape(y,(-1,1)))
   

5. 模型预测

   # 模型预测
   y_pred =lr.predict(np.reshape(x,(-1,1)))
   

6. 数据可视化

   # 数据可视化
   plt.figure(figsize=(5,5))  # 产生一个窗口
   plt.scatter(x,y)  # 画散点图
   plt.plot(x,y_pred,color='red')
   plt.show()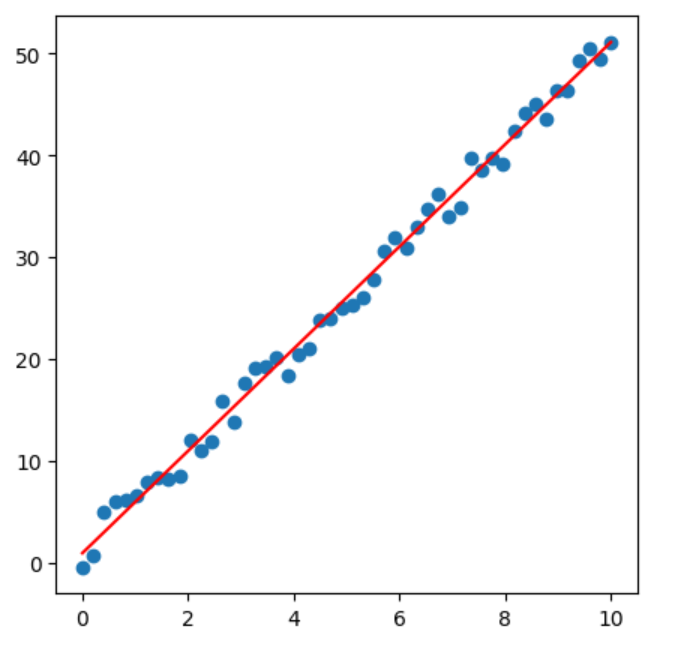
   

   

7. 模型评估

   # 模型评估
   # The mean squared error
   print("Mean squared error: %.2f" % mean_squared_error(np.reshape(y,(-1,1)), y_pred))
   # The coefficient of determination: 1 is perfect prediction
   print("Coefficient of determination: %.2f" % r2_score(np.reshape(y,(-1,1)), y_pred))
   

   Mean squared error: 1.47
   Coefficient of determination: 0.99

8. 打印权重

   # 打印权重
   print("Coefficients: ", lr.coef_)
   print("Intercept: ", lr.intercept_)
   

   Coefficients: [[5.01215851]]
   Intercept: [0.99046872]

3.2 多变量线性回归

本例中使用 sklearn 提供的一个内置的糖尿病数据集 (diabetes dataset)，它通常用于回归分析的教学示例。这个数据集包含442个患者的10个生理特征以及一年后疾病级别的量化指标。详情请查看：

• 【sklearn实战】datasets数据集简介
• 【sklearn实战】sklearn 数据集之 Toy datasets

# 导入所需的库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np

# 加载糖尿病数据集
diabetes = datasets.load_diabetes()

# 使用所有特征
X = diabetes.data
y = diabetes.target

# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归对象
regr = LinearRegression()

# 训练模型
regr.fit(X_train, y_train)

# 预测测试集的结果
y_pred = regr.predict(X_test)

# 输出结果
print("Coefficients: \n", regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print("Coefficient of determination (R^2): %.2f" % r2_score(y_test, y_pred))

# 如果需要查看更详细的模型信息，可以输出以下内容
print("Intercept: ", regr.intercept_)
print("Feature names: ", diabetes.feature_names)

# 输出
Coefficients: 
 [  37.90402135 -241.96436231  542.42875852  347.70384391 -931.48884588
  518.06227698  163.41998299  275.31790158  736.1988589    48.67065743]
Mean squared error: 2900.19
Coefficient of determination (R^2): 0.45
Intercept:  151.34560453985995
Feature names:  ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

这段代码首先加载了糖尿病数据集，并将其分为训练集和测试集。然后，创建了一个线性回归模型并用训练集对其进行拟合。最后，它在测试集上预测了目标变量，并计算了均方误差（MSE）和决定系数（R2R2），以评估模型的表现。