双边滤波(Bilateral filter)是一种非线性的滤波方法,是结合图像的空间邻近度和像素值相似度的一种折中处理,同时考虑空域信息和灰度相似性,达到保边去噪的目的。具有简单、局部的特点。双边滤波器的好处是可以做边缘保存。
将双边滤波应用到点云中,其算法流程如下:

%% 双边滤波
clear all
%% 生成带噪声的点云
gv = 0:0.01:1;
[X,Y] = meshgrid(gv,gv);
% X(:)的意思是把矩阵转换为一行
p = [X(:),Y(:),0.5*ones(numel(X),1)];
% 生成噪声,随机生成500个噪声点
noise = rand(500, 3);
% 合并,p的矩阵为n*3
p = [p;noise];
clear X Y noise gv
% pcshow(p)
%% 计算法向量
% r半径搜索,单位m
r = 1;
% 搜索得到全部的r内临近点
[idx,d] = rangesearch(p,p,r,'Distance','euclidean','NSMethod','kdtree');
% 可以通过pcnormals实现法向量的提取,这个是matlab2019b函数自带的法向量计算函数
% p = pointCloud(p); % p需要先转换成matlab读取的格式
% vec = pcnormals(p); % 这样就可以计算法向量,是通过最邻近点计算的,默认是8个临近点
% p = p.Location; % p还原数组格式
% Reig为按照圆搜索邻近点计算法向量,博主自写的函数。
[~,~,~,~,~,vec] = Reig(p, r);
% 权重因子
% sum_w = 0;
% sum_pr = 0;
% pd为每个点到其邻近点的影响因子
pd = r;
% 每个点到临近点法式的影响因子
% pn = 0.5;
% 循环计算每个点的权重
for i = 1:length(p(:,1))
% 权重因子
sum_w = 0;
sum_pr = 0;
% 提取当前点
a = p(i,:);
% 得到当前点r范围内的点
curp = idx(i,:);
% cell转换为数组mat
curp = cell2mat(curp);
% 第一个索引是自己,所以去除
curp = curp(:,2:end);
% 求取临近点距离标准差
didx = d(i,:);
didx = cell2mat(didx);
didx = didx(:,2:end);
pn = std(didx);
% 搜索索引点
idxpoint = p(curp,:);
% 循环领域内的点
for j = 1:length(curp)
% 领域点的当前点
b = idxpoint(j,:);
% 空间权重之一
dd = norm(b-a);
% 空间权重之二
dn = dot(b-a,vec(i,:));
%
w = exp(-dd^2/(2*pd^2))*exp(-dn^2/(2*pn^2));
%
sum_pr = sum_pr + w * dn;
%
sum_w = sum_w + w;
end
qp = sum_pr/sum_w;
p1(i,:) = p(i,:) + qp * vec(i,:);
end
% qp = sum_pr/sum_w;
% % 平滑数据处理
% for i = 1:length(p(:,1))
% p1(i,:) = p(i,:) + qp * vec(i,:);
% end
pcshow(p1)
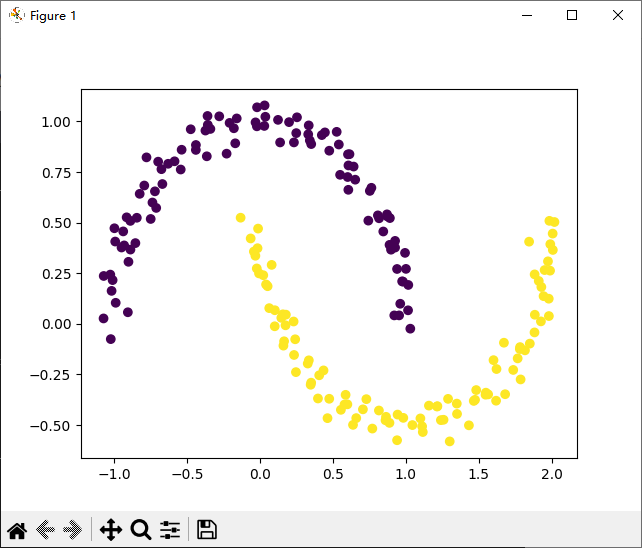
下图是生成的带噪声的数据:
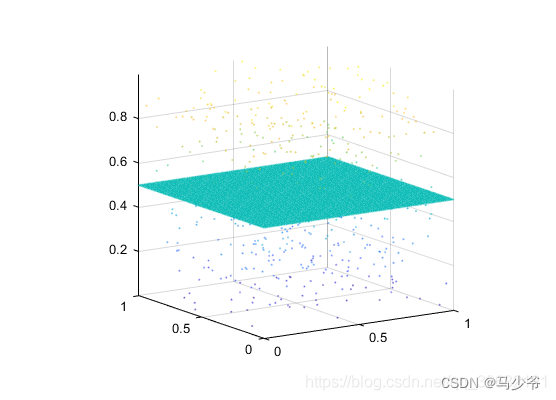

经过双边滤波过后:
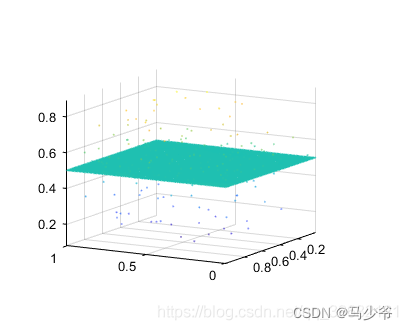

双边滤波原文“The Bilateral Filter for Point Clouds",作者为 Julie Digne、 Carlo Franchis。由于双边滤波原理简单,其实现过程并不复杂,因此本文不对其原理进行详细说明和解释,有兴趣的小伙伴可以直接下载论文进行详细阅读。本文旨在分析双边滤波的适应范围及其不足之处。
下面直接给出论文中单点更新的方法:

通过单点更新公式可知,更新点为原始点在法线方向上的移动。作者在此处进行了说明,通过半径搜索得到的邻域点集进行法线估计,法线无需进行定向,其原因在于邻域点与原始点构成的向量,在与法线进行点乘时已经包含了原始点需要移动的正确方向(感兴趣的同学,可以在纸上简单的画一下,就会明白)。
现在考虑两个权重项,距离权重、法线方向投影模长权重,在整个算法的伪代码中作者给出了权重的计算方法:

通过公式可知,作者使用两个高斯分布,其中距离越近权重越大,反之,距离越远权重越小。关于法线方向投影模长权重亦是如此。权重的作用在于用来保证局部点云即能平滑又不失其特征,故而使距离远,法线方向上投影模长大的点权重变小。
在本人“点云法线计算”一文中对法线的计算进行了说明,由该文可知,法线的估算采用的是平面方程。故而对双边滤波而言其平滑模型为平面模型,因此使用该方法进行平滑时,无论怎么调节参数其本质都不会改变。因此在使用该方法进行平滑时,对于边、角、特征锐利之处都会被袜平,对于要求平滑前后变化较小且特征保持良好的需求而言,双边滤波因此失去了适用性。其实对于局部点云为非平面,采用平面估计法线已经失去了局部的特征。
为此有学者采用距离权重的方式修改点云法线计算过程中的协方差,来提高法线估计的准确性。当然采用该方法会有一些改进,但是仍旧改变不了其本质因此上述现象仍旧会存在。采用加权协方差计算出的整体模型法线过渡不均匀,会使整体模型平滑效果变差。
在本人实践经验中,目前只有国外的GeoMagic的平滑效果最佳、细节保持最好。有兴趣的小伙伴可以查看其专利,专利中给出了其平滑的策略和方法,采用法线协方差分解后特征值度量的分类方法进行平滑,其中采用平面方程,二次曲面方程,圆锥曲线方程进行拟合。这里需要指出的是,分类后类与类的接缝处会出现台阶,如何对其进行处理是一个相当棘手的问题,显然GeoMagic的处理方法很到位。同样需要说明的是本人按二次曲面拟合方法进行了局部区域点云平滑实验,不管是计算速度上还是效果上都不如GeoMagic,当然比双边滤波要好很多,所以猜测专利给出的是一种方法其实际使用方法并不是专利中的,又或只是部分,也有可能是本人实现错误。
参考文献:
https://blog.csdn.net/qq_33029733/article/details/106909683
https://blog.csdn.net/qq_39632121/article/details/119113362