基于嵌入-对比学习的联邦知识图谱补全

1 引言

1.1 现存问题

在联邦学习中，跨客户端的数据异质性(即非相同分布的数据)是主要挑战，因为当数据异质性存在时，本地目标可能与全局目标不同。

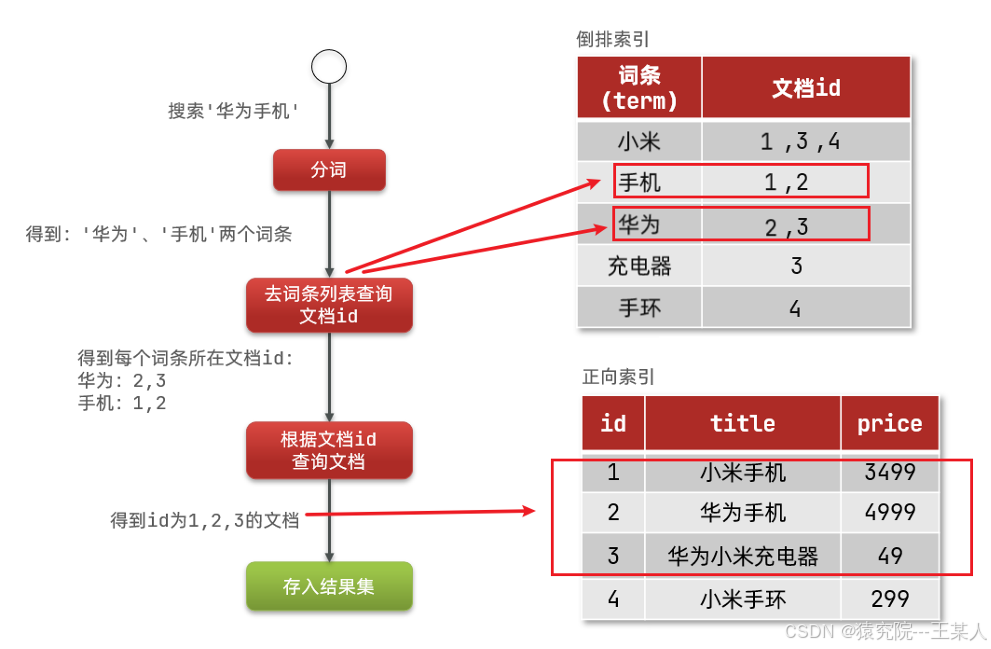
如图所示，School KG中的三元组表示Bob和Jack的学术信息，而ecommerce KG中的三元组表示他们的购物信息。然而，先前的方法FedE将fedag应用于知识图嵌入，没有考虑知识图在联邦设置下的异构性问题。

1.2 解决方案

为了解决联邦知识图补全中知识图嵌入学习的数据异构性问题，提出了一种基于嵌入-对比学习的联邦知识图补全框架FedEC。

FedEC通过学习共享实体嵌入来实现知识图嵌入的协同优化，不同于传统方法需要汇集所有三元组数据，这种方法有效地保护了数据隐私，同时提高了嵌入表示的性能。

2 FedEC框架

2.1 相关定义

定义一组联邦知识图为 $\mathcal{G}^{Fed}=\{\mathcal{G}^{i}\}_{i=1}^{C}$ ，其中 $\mathcal{G}^{i}=\{\mathcal{E}^{i},\mathcal{R}^{i},\mathcal{T}^{i}\}$ 为位于客户端i的知识图谱，C为客户端数量。更准确地说，每个知识图的实体集与其他客户的一个或多个实体集重叠，这是这些联合知识图能够利用其他知识图来完成自己的先决条件。

假设关于对齐实体的信息由私有集合交集给出(这是一个加密技术，用于在多个参与方之间找出共有的元素集合，同时不泄露其他非共有的元素)，并私有地保存在主服务器中。此外，像其他一些联邦学习工作一样，隐私不是重点，一些标准的隐私保护方法可以自然地适应我们的框架。客户端之间所有唯一实体的实体集在服务器中保存为 $\mathcal{E}^{Fed}$ 。

2.2 FedEC

在FedEC中，不同知识图谱共享实体的知识图谱嵌入是通过聚合客户端局部三元组训练的嵌入来全局学习的。全局学习的嵌入可以从各种联合知识图中吸收信息，而不显式地收集它们的三元组。具体而言，对于每个具有知识图的客户端，使用嵌入学习器仅基于该客户端的三元组学习有效的知识图嵌入。此外，主服务器用于协调嵌入聚合。换句话说，实体嵌入是通过客户端的三元组在本地学习的，主服务器用于对来自客户端的实体嵌入进行平均。

2.2.1 初级嵌入学习

为了展示框架的通用性，选择了五种具有代表性的知识图嵌入方法作为嵌入学习器，包括平移距离模型(TransE和RotatE)、语义匹配模型(DistMult和ComplEx)和基于gnn的模型(R-GCN)。

2.2.2 局部客户端嵌入训练

以一个客户端 $\mathcal{G}^{c} = \{\mathcal{E}^{c},\mathcal{R}^{c},\mathcal{T}^{c}\}$ 为例，这个过程对于不同的客户端是相同的。

在第t轮中，客户端从主服务器接收全局实体嵌入Et(在每一轮训练开始时，主服务器会将当前的全局模型参数——在这里是实体嵌入Et，发送给参与这一轮训练的所有客户端。这些参数代表了所有客户端之前训练结果的汇总)，在局部训练中更新嵌入的过程类似于使用传统KGE方法训练知识图嵌入。局部训练的损失函数：

$p(h,r,t_j^\prime)$ 是自对抗性负采样中 $(h,r,t_j')$ 的权重，定义是 $p(h,r,t_j')=\frac{\exp(\beta s(h,r,t_j'))}{\sum_i\exp(\beta s(h,r,t_i'))}$

其中 𝛽 是采样的温度。

主服务器上的全局实体嵌入 $\mathbf{E}_{t}$ 将根据客户 c 中的三元组更新为客户 c 特定的实体嵌入 $\mathbf{E}_{t}^{c}$ 。在更新 $\mathbf{E}_{t}^{c}$ 时，我们希望增加 $\mathbf{E}_{t}^{c}$ 和 $\mathbf{E}_{t}$ 之间的相似度，减少 $\mathbf{E}_{t}^{c}$ 和上一轮 $\mathbf{E}_{t-1}^{c}$ 之间的相似度，这里被称为对比学习。我们使用类似 NT-Xent 损失的模型对比联邦学习提出的损失函数，如下：

其中 𝜏是温度参数，sim⁡(⋅,⋅)是余弦相似度函数。

总体而言，在本地训练期间，我们将对比损失和 KGE 损失结合起来作为损失，一组三元组𝑇的损失定义为： $L(\mathcal{T})=\sum_{(h,r,t)\in\mathcal{T}}L_{kge}(h,r,t)+\mu L_{con}$ ，其中𝜇是控制对比损失重要性的权重。

为什么减少 $\mathbf{E}_{t}^{c}$ 和上一轮 $\mathbf{E}_{t-1}^{c}$ 之间的相似度？

主要是为了促进模型的学习和避免过拟合到单一客户端的数据。以下是几个关键原因：

鼓励学习新信息：通过减少与上一轮嵌入的相似度，模型被迫去学习和捕捉当前轮次中新的、未见过的信息。这有助于确保模型不仅依赖于先前学习的模式，而且能够适应和整合来自不同客户端的新知识。
避免过拟合：在联邦学习中，每个客户端只基于自己的数据集进行训练。减少与上一轮嵌入的相似度有助于防止模型在某个特定客户端的数据集上过拟合，从而提高模型的泛化能力。
促进知识迁移：在联邦学习的上下文中，目标是让模型能够从所有参与者的数据中学习，即使数据分布是非独立同分布（non-iid）的。减少与上一轮嵌入的相似度有助于模型在不同客户端之间迁移和综合知识，从而提高整个系统的性能和鲁棒性。
增强模型多样性：通过对比学习，减少与上一轮嵌入的相似度可以增加模型的多样性，使得模型在面对不同的任务和数据时能有更广泛的适应能力。

然而，值得注意的是，这种机制需要谨慎设计，以确保不会破坏模型的稳定性。过度减少相似度可能会导致模型不稳定或者丢失已经学到的有用信息。因此，通常会有一个平衡参数（例如公式中的 𝜇μ），用来控制对比损失的重要性，确保模型既能学习新知识，又不会遗忘旧知识。

2.2.3 更新全局嵌入

在训练过程中，迭代地进行局部训练和全局更新的过程，一次迭代称为一轮。在每一轮中，都会选出一部分客户进行本地培训，我们将这部分被选中的客户称为 $c_{sel}$ 。根据之前的联邦学习算法FedAvg，我们将不同客户端的实体嵌入聚合到主服务器的全局实体嵌入，取平均值如下:

$\mathbf{E}_{t}^{c}$ 是在第 t 轮基于客户 c 知识图谱的本地训练后的实体嵌入矩阵。如果 $\mathbf{E}_{t+1}$ 的第 i 行所表示的实体不存在于客户 c，则 $\mathbf{E}_{t}^{c}$ 的第 i 行元素全为零。此外， $\mathbf{E}_{t+1}$ 和 $\mathbf{E}_{t}^{c}$ 都是形状为 $n_{e}$ ×𝑑的矩阵，其中 $n_{e}$ 是联合知识图谱 $\mathcal{G}^{Fed}$ 集合中所有唯一实体的数量，即 $n_{e} = |\mathcal{E}^{Fed}| = |\cup_{i=1}^{C}\mathcal{E}^{i}|$ 。

d 是嵌入维度。另外，n 是一个向量，包含 $\mathcal{C}^{sel}$ ∣个元素，每个元素 𝑛_𝑖表示包含由 $\mathbf{E}_{t+1}$ 第 i 行表示的实体（即实体 𝐸_𝑖𝐹𝑒𝑑）的客户的数量。确切地说，n 的每个元素定义为：它记录了第 t+1 轮全局知识图谱中每个实体在选定客户集合 $\mathcal{C}^{sel}$ 中出现的次数。具体地，n 向量的第 i 个元素 𝑛_𝑖计算方式如下：

2.2.4 局部训练和全局更新

2.2.5 嵌入集成过程

问题：

每个客户端通过FedEC优化得到的嵌入是全局优化的结果，可能会偏离仅基于本地三元组优化得到的局部最小值。因此，每个客户端的嵌入信息可能与传统方法有所不同，导致信息不一致。

解决方案：

为了结合这两种嵌入的能力，我们提出了两种嵌入集成方案。具体方法是结合两种嵌入输出的分数，这激励我们设计了两种嵌入集成方法：直接集成和自适应集成。

直接集成（Direct Ensemble）：
- 直接将两种嵌入的分数进行组合。
- 这种方法简单直接，将全局嵌入和本地嵌入的结果加权平均或其他方式结合。
自适应集成（Adaptive Ensemble）：
- 根据某些准则或动态调整，灵活组合两种嵌入的分数。
- 这种方法更为灵活，可以根据具体情况调整两种嵌入的权重，达到更好的集成效果。

还可以基于一组不同的嵌入学习器来联合收割机s（fed）（·）和s（sig）（·），我们将其称为FedEC+。在FedEC+中，直接集成的计算如下：

与公式(13)区别总结

嵌入方法的数量：
- 公式(13)仅仅对两种嵌入方法的分数取平均。
- 公式(15)对多个嵌入方法的分数取平均，并且包括了多种嵌入学习方法的组合。
计算复杂度：
- 公式(13)的计算相对简单，只涉及两种嵌入方法的分数。
- 公式(15)的计算复杂度较高，因为它需要对多个嵌入学习方法的分数进行计算和平均。
适用性：
- 公式(13)适用于简单的场景，只需要结合两种嵌入方法。
- 公式(15)适用于更复杂的场景，需要结合多种嵌入方法，以提高模型的鲁棒性和性能。

FedEC+的自适应集成如下：

与公式(14)区别总结

嵌入方法的数量：
- 公式(14)仅仅对两种嵌入方法（FedEC和单个知识图）的分数进行加权。
- 公式(16)则对多种嵌入方法（例如 TransE、RotatE 等）进行加权组合，考虑了更多的嵌入信息。
权重参数的复杂度：
- 公式(14)有两个权重参数 wfw^{f}wf 和 wsw^{s}ws。
- 公式(16)有针对每个嵌入学习方法的权重参数 welfw^{f}_{el}welf 和 welsw^{s}_{el}wels，因此参数更多，模型更为复杂。
灵活性和适用性：
- 公式(14)适用于仅需结合两种嵌入方法的场景，较为简单。
- 公式(16)适用于需要结合多种嵌入方法的场景，能够提供更高的灵活性和性能。