【神经网络】梯度下降的优化方法【数学公式+代码示例】

文章目录

1、简介
2、指数加权平均
- 2.1、公式
- 2.2、代码
3、Momentum⭐
- 3.1、公式演变
- 3.2、代码
4、AdaGrad
- 4.1、计算步骤
- 4.2、代码示例
5、RMSProp
- 5.1、公式
- 5.2、代码
- 5.3、小结
6、Adam
- 6.1、公式和步骤解释⭐
- 6.2、代码⭐
- 6.3、优点
7、何为鞍点
8、小结

🍃作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎人工智能和前端开发。
🦅个人主页：@逐梦苍穹
📕所属专栏：人工智能
🌻gitee地址：xzl的人工智能代码仓库
✈ 您的一键三连，是我创作的最大动力🌹

1、简介

传统的梯度下降优化算法中，可能会碰到以下情况：
碰到平缓区域，梯度值较小，参数优化变慢，碰到 “鞍点” ，梯度为 0，参数无法优化，碰到局部最小值。
对于这些问题, 出现了一些对梯度下降算法的优化方法，例如：Momentum、AdaGrad、RMSprop、Adam 等.

2、指数加权平均

我们最常见的算数平均指的是将所有数加起来除以数的个数，每个数的权重是相同的。
加权平均指的是给每个数赋予不同的权重求得平均数。
移动平均数，指的是计算最近邻的 N 个数来获得平均数。
指数移动加权平均则是参考各数值，并且各数值的权重都不同，距离越远的数字对平均数计算的贡献就越小（权重较小），距离越近则对平均数的计算贡献就越大（权重越大）。
比如：明天气温怎么样，和昨天气温有很大关系，而和一个月前的气温关系就小一些。

2.1、公式

计算公式可以用下面的式子来表示： $S_t = \begin{cases} Y_1, & \text{t = 0} \\ \beta \ast S_{t-1} + (1 - \beta) \ast Y_t, & \text{t > 0} \end{cases} ]$

$S_t$ 表示指数加权平均值;
$Y_t$ 表示 t 时刻的值;
$β$ 调节权重系数，该值越大平均数越平缓。

2.2、代码

我们接下来通过一段代码来看下结果，我们随机产生进 30 天的气温数据：

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/29 1:34
import torch
import matplotlib.pyplot as plt

ELEMENT_NUMBER = 30  # 定义温度数据的天数


# 1. 实际平均温度
def test01():
    # 固定随机数种子，确保每次运行结果一致
    torch.manual_seed(0)

    # 产生30天的随机温度数据，温度服从正态分布，均值为0，标准差为10
    temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10
    print(temperature)

    # 生成代表天数的数组，从1到30
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)

    # 绘制温度变化曲线
    plt.figure()
    plt.plot(days, temperature, color='r')
    plt.scatter(days, temperature)  # 绘制散点图
    plt.xlabel('Days')  # X轴标签
    plt.ylabel('Temperature')  # Y轴标签
    plt.title('Actual Temperature Over 30 Days')  # 图标题
    # plt.show()


# 2. 指数加权平均温度
def test02(beta=0.9):
    # 固定随机数种子，确保每次运行结果一致
    torch.manual_seed(0)

    # 产生30天的随机温度数据，温度服从正态分布，均值为0，标准差为10
    temperature = torch.randn(size=[ELEMENT_NUMBER, ]) * 10
    print(temperature)

    exp_weight_avg = []  # 存储指数加权平均温度的列表

    # 计算每一天的指数加权平均温度
    for idx, temp in enumerate(temperature, 1):

        # 第一个元素的 EWA 值等于自身
        if idx == 1:
            exp_weight_avg.append(temp)
            continue

        # 第二个及之后的元素的 EWA 值等于上一个 EWA 乘以 β + 当前温度乘以 (1-β)
        new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * temp
        exp_weight_avg.append(new_temp)

    # 生成代表天数的数组，从1到30
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)

    # 绘制指数加权平均温度变化曲线
    plt.figure()
    plt.plot(days, exp_weight_avg, color='r')
    plt.scatter(days, temperature)  # 绘制实际温度的散点图
    plt.xlabel('Days')  # X轴标签
    plt.ylabel('Temperature')  # Y轴标签
    plt.title(f'Exponentially Weighted Average Temperature (beta={beta})')  # 图标题，包含beta值
    # plt.show()


if __name__ == '__main__':
    # 调用test01函数，绘制实际温度图
    test01()
    # 调用test02函数，绘制beta为0.5的EWA温度图
    test02(0.5)
    # 调用test02函数，绘制beta为0.9的EWA温度图
    test02(0.9)
    plt.show()

程序结果如下：

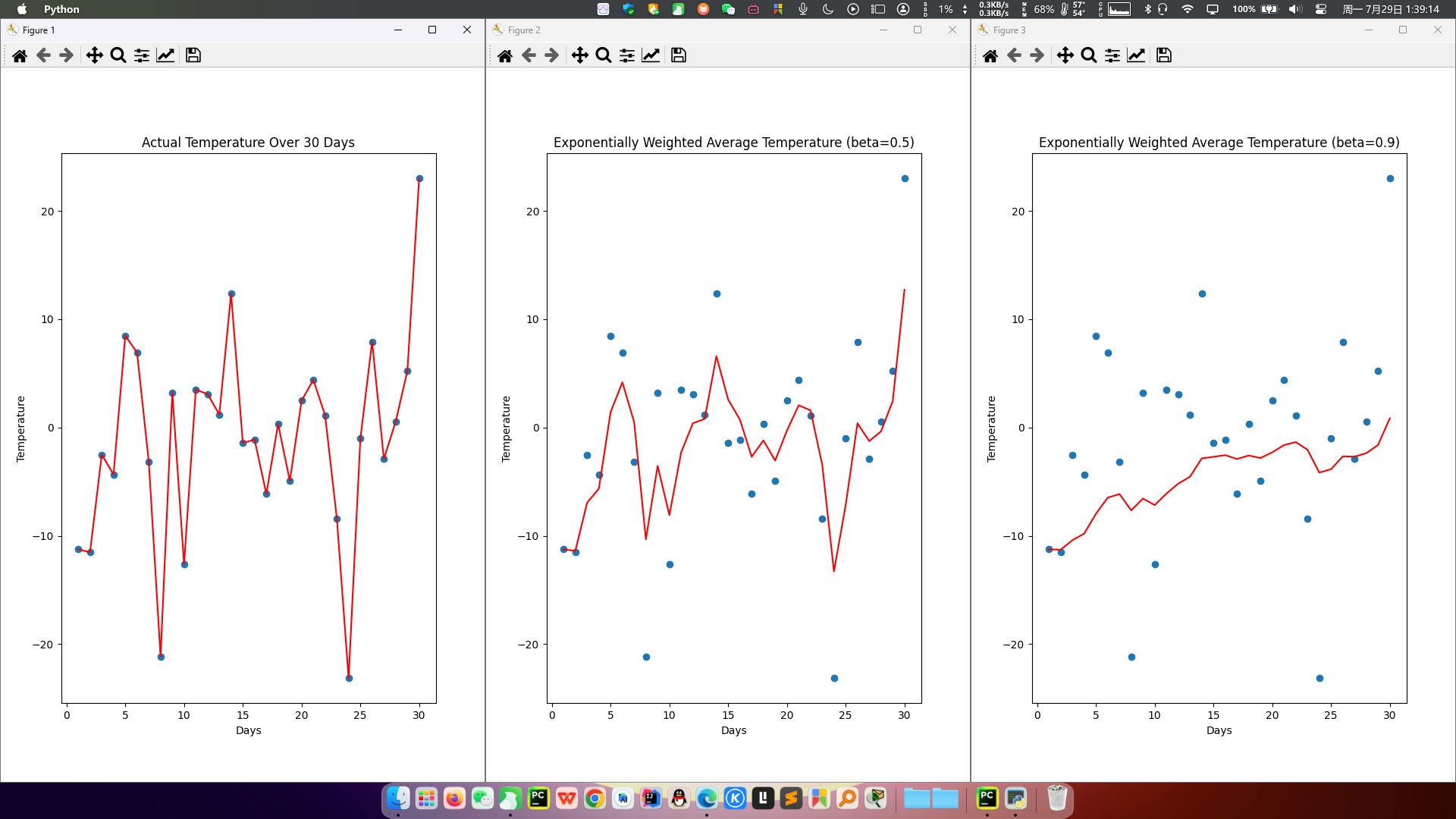
从程序运行结果可以看到：
指数加权平均绘制出的气氛变化曲线更加平缓;
β 的值越大，则绘制出的折线越加平缓; β 值一般默认都是 0.9.

3、Momentum⭐

Momentum->动量

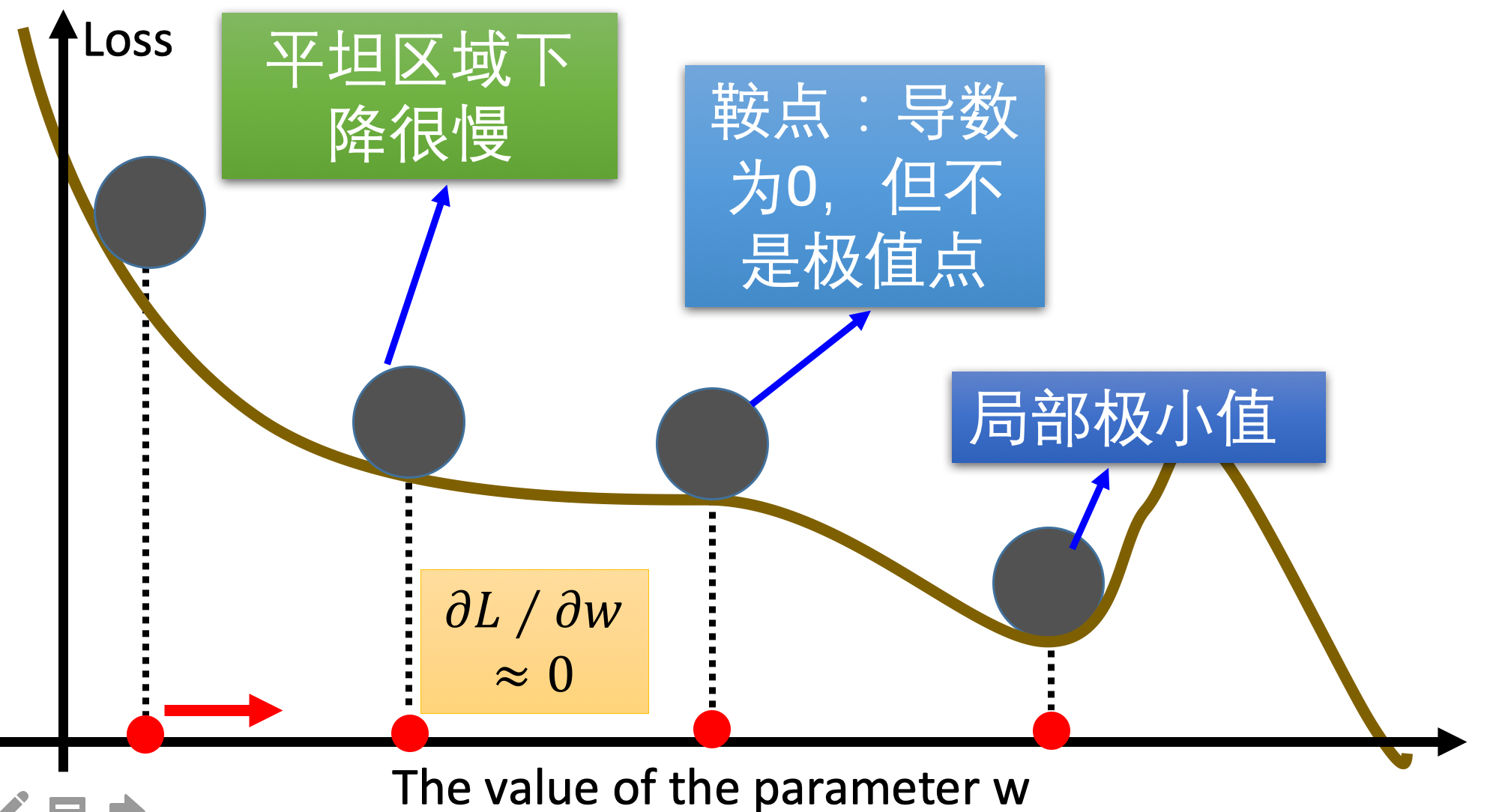
当梯度下降碰到 “峡谷” 、”平缓”、”鞍点” 区域时, 参数更新速度变慢。
Momentum 通过指数加权平均法，累计历史梯度值，进行参数更新，越近的梯度值对当前参数更新的重要性越大。

3.1、公式演变

梯度的指数加权平均（Exponential Moving Average, EMA）的一般公式如下：
$S_t = \beta S_{t-1} + (1 - \beta) D_t$
其中：

$S_t$ ：当前时刻的加权移动平均值
$S_{t-1}$ ：上一个时刻的加权移动平均值
$D_t$ ：当前时刻的梯度值
$\beta$ ：权重系数（0 到 1 之间的值）

解释：

$S_{t-1}$ 表示历史梯度的移动加权平均值（上一个时刻的 EMA）。
$D_t$ 表示当前时刻的梯度值。
$\beta$ 为权重系数，表示历史梯度与前 EMA 中的权重。

咱们举个例子，假设：权重 $\beta$ 为 0.9，例如：
第一次梯度值： $s_1 = d_1 = w_1$
第二次梯度值： $s_2 = 0.9 \ast s_1 + d_2 \ast 0.1$
第三次梯度值： $s_3 = 0.9 \ast s_2 + d_3 \ast 0.1$
第四次梯度值： $s_4 = 0.9 \ast s_3 + d_4 \ast 0.1$

$w$ 表示初始梯度
$d$ 表示当前轮数计算出的梯度值
$s$ 表示历史梯度值

梯度下降公式中梯度的计算，就不再是当前时刻 $t$ 的梯度值，而是历史梯度值的指数移动加权平均值。
公式修改为： $W_{t+1} = W_t - \alpha \ast D_t$
那么，Monmentum 优化方法是如何一定程度上克服 “平缓”、”鞍点”、”峡谷” 的问题呢？

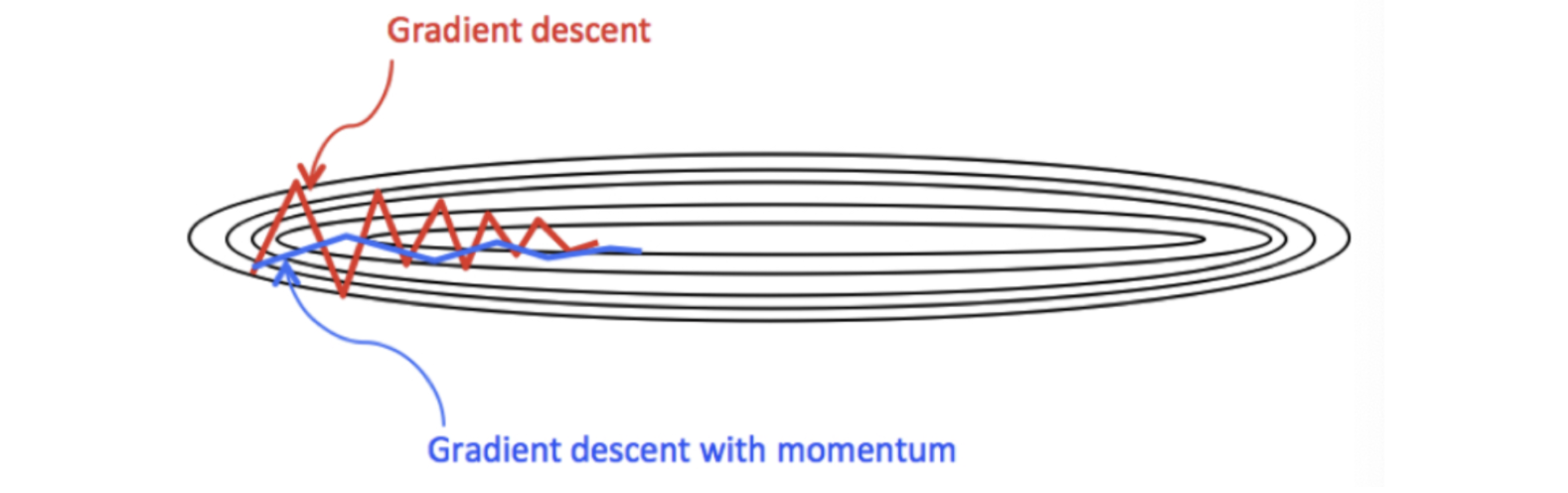
当处于鞍点位置时，由于当前的梯度为 0，参数无法更新。
但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值，很有可能使得跨过鞍点。
由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进方向，可能会出现震荡，使得训练时间变长。
Momentum 使用移动加权平均，平滑了梯度的变化，使得前进方向更加平缓，有利于加快训练过程。一定程度上有利于降低 “峡谷” 问题的影响。

峡谷问题：就是会使得参数更新出现剧烈震荡

Momentum 算法可以理解为是对梯度值的一种调整，我们知道梯度下降算法中还有一个很重要的学习率，Momentum 并没有学习率进行优化。

3.2、代码

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/29 2:23
import numpy as np
import matplotlib.pyplot as plt

# 初始化参数
theta = np.random.randn(2)  # 假设我们有两个参数，随机初始化
alpha = 0.1  # 初始学习率
beta = 0.9  # 动量系数
velocity = np.zeros_like(theta)  # 初始化动量为零向量


# 定义一个简单的二次损失函数
def loss_function(theta):
    return theta[0] ** 2 + theta[1] ** 2  # 损失函数：J(θ) = θ[0]^2 + θ[1]^2


# 计算梯度
def compute_gradient(theta):
    return 2 * theta  # 梯度：∇J(θ) = [2*θ[0], 2*θ[1]]


# 进行梯度下降迭代
iterations = 100  # 设定迭代次数
theta_history = []  # 存储每次迭代的theta值
loss_history = []  # 存储每次迭代的损失值

for _ in range(iterations):
    gradient = compute_gradient(theta)  # 计算梯度
    velocity = beta * velocity + (1 - beta) * gradient  # 更新动量项 v_t = β * v_{t-1} + (1 - β) * g_t
    theta -= alpha * velocity  # 更新参数 θ = θ - α * v_t

    # 记录参数和损失值以便后续绘图
    theta_history.append(theta.copy())  # 记录当前theta值
    loss_history.append(loss_function(theta))  # 记录当前损失值

    print(f"Updated parameters: {theta}, Loss: {loss_function(theta)}")  # 打印当前参数和损失值

print(f"Optimized parameters: {theta}")  # 打印最终优化后的参数

# 绘制参数更新轨迹
theta_history = np.array(theta_history)  # 将theta历史记录转换为NumPy数组
plt.figure(figsize=(12, 6))  # 创建一个12x6英寸的图形

plt.subplot(1, 2, 1)  # 创建1行2列的子图，选择第一个子图
plt.plot(theta_history[:, 0], theta_history[:, 1], 'o-', markersize=4)  # 绘制theta[0]和theta[1]的变化轨迹
plt.title('Parameter Update Path with Momentum')  # 设置子图标题
plt.xlabel('Theta[0]')  # 设置x轴标签
plt.ylabel('Theta[1]')  # 设置y轴标签

# 绘制损失函数值变化
plt.subplot(1, 2, 2)  # 选择第二个子图
plt.plot(loss_history, 'r-')  # 绘制损失值变化曲线，红色实线
plt.title('Loss Function Value with Momentum')  # 设置子图标题
plt.xlabel('Iteration')  # 设置x轴标签
plt.ylabel('Loss')  # 设置y轴标签

plt.tight_layout()  # 自动调整子图布局
plt.show()  # 显示图形

结果：

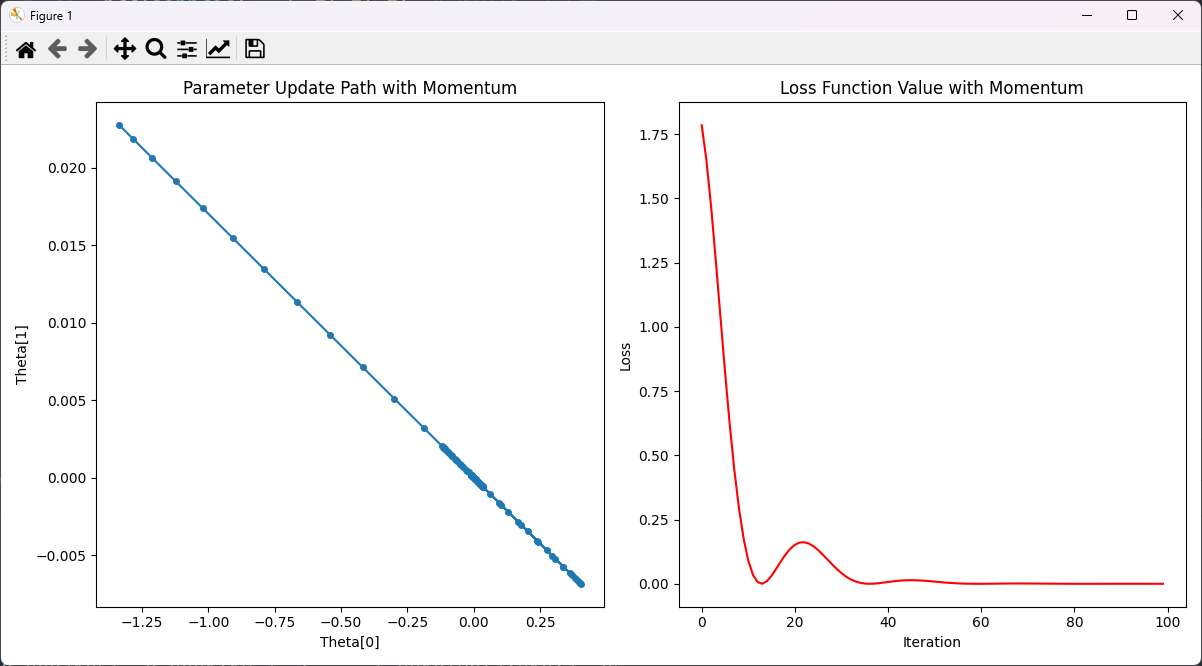
解释：

损失函数值在初始时较高，随着迭代次数的增加，损失值迅速下降。
在前几次迭代中，损失值下降速度非常快，这是因为动量法在初始阶段累积了较大的梯度，使得参数更新步长较大。
在迭代到大约20次时，损失值出现了一些波动，这是动量法的特性导致的，它在接近极小值时可能会因累积的动量过大而出现短暂的反弹。
最终，损失值趋于平稳，表明模型参数已接近最优值，优化过程收敛。

4、AdaGrad

AdaGrad 通过对不同的参数分量使用不同的学习率，AdaGrad 的学习率总体会逐渐减小。
这是因为 AdaGrad 认为：在起初时，我们距离最优目标仍较远，可以使用较大的学习率，加快训练速度，随着迭代次数的增加，学习率逐渐下降。

4.1、计算步骤

AdaGrad计算步骤如下：

初始化
- 初始学习率 $\alpha$
- 初始参数 $\theta$
- 小常数 $\epsilon$ ，通常为 $\times 10^{-6}$
- 初始化梯度累积变量 $s = 0$
从训练集中采样
- 从训练集中采样 $m$ 个样本的小批量，计算梯度 $g$
累积平方梯度
- 更新累积平方梯度： $\odot g$
  其中， $\odot$ 表示逐个分量相乘（即逐元素相乘）
调整学习率
- 根据累积平方梯度调整学习率 $\alpha$ ： $\alpha_t = \frac{\alpha}{\sqrt{s + \epsilon}}$
更新参数
- 使用调整后的学习率更新参数 $\theta$ ： $\theta = \theta - \alpha_t \odot g$
重复步骤2-5
- 继续重复步骤2-5，直到满足停止条件（如迭代次数或误差足够小）

参数更新公式如下：

累积平方梯度公式： $\odot g$
调整学习率公式： $\alpha_t = \frac{\alpha}{\sqrt{s + \epsilon}}$
参数更新公式： $\theta = \theta - \alpha_t \odot g$

4.2、代码示例

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/29 2:08

import numpy as np  # 导入NumPy库，用于数值计算
import matplotlib.pyplot as plt  # 导入Matplotlib库，用于绘图

# 初始化参数
theta = np.random.randn(2)  # 假设我们有两个参数，随机初始化
alpha = 0.1  # 初始学习率
eps = 1e-10  # 防止除零的小常数
s = np.zeros_like(theta)  # 初始化累积梯度平方和为与theta相同形状的零向量

# 定义一个简单的二次损失函数
def loss_function(theta):
    return theta[0]**2 + theta[1]**2  # 损失函数：J(θ) = θ[0]^2 + θ[1]^2

# 计算梯度
def compute_gradient(theta):
    return 2 * theta  # 梯度：∇J(θ) = [2*θ[0], 2*θ[1]]

# 进行梯度下降迭代
iterations = 100  # 设定迭代次数
theta_history = []  # 存储每次迭代的theta值
loss_history = []  # 存储每次迭代的损失值

for _ in range(iterations):
    gradient = compute_gradient(theta)  # 计算梯度
    s += gradient**2  # 更新累积梯度平方和 s = s + g_t ⊙ g_t
    adjusted_alpha = alpha / (np.sqrt(s) + eps)  # 调整学习率 α_t = α / (√s + ε)
    theta -= adjusted_alpha * gradient  # 更新参数 θ = θ - α_t ⊙ g_t

    # 记录参数和损失值以便后续绘图
    theta_history.append(theta.copy())  # 记录当前theta值
    loss_history.append(loss_function(theta))  # 记录当前损失值

    print(f"Updated parameters: {theta}, Loss: {loss_function(theta)}")  # 打印当前参数和损失值

print(f"Optimized parameters: {theta}")  # 打印最终优化后的参数

# 绘制参数更新轨迹
theta_history = np.array(theta_history)  # 将theta历史记录转换为NumPy数组
plt.figure(figsize=(12, 6))  # 创建一个12x6英寸的图形

plt.subplot(1, 2, 1)  # 创建1行2列的子图，选择第一个子图
plt.plot(theta_history[:, 0], theta_history[:, 1], 'o-', markersize=4)  # 绘制theta[0]和theta[1]的变化轨迹
plt.title('Parameter Update Path')  # 设置子图标题
plt.xlabel('Theta[0]')  # 设置x轴标签
plt.ylabel('Theta[1]')  # 设置y轴标签

# 绘制损失函数值变化
plt.subplot(1, 2, 2)  # 选择第二个子图
plt.plot(loss_history, 'r-')  # 绘制损失值变化曲线，红色实线
plt.title('Loss Function Value')  # 设置子图标题
plt.xlabel('Iteration')  # 设置x轴标签
plt.ylabel('Loss')  # 设置y轴标签

plt.tight_layout()  # 自动调整子图布局
plt.show()  # 显示图形

结果：

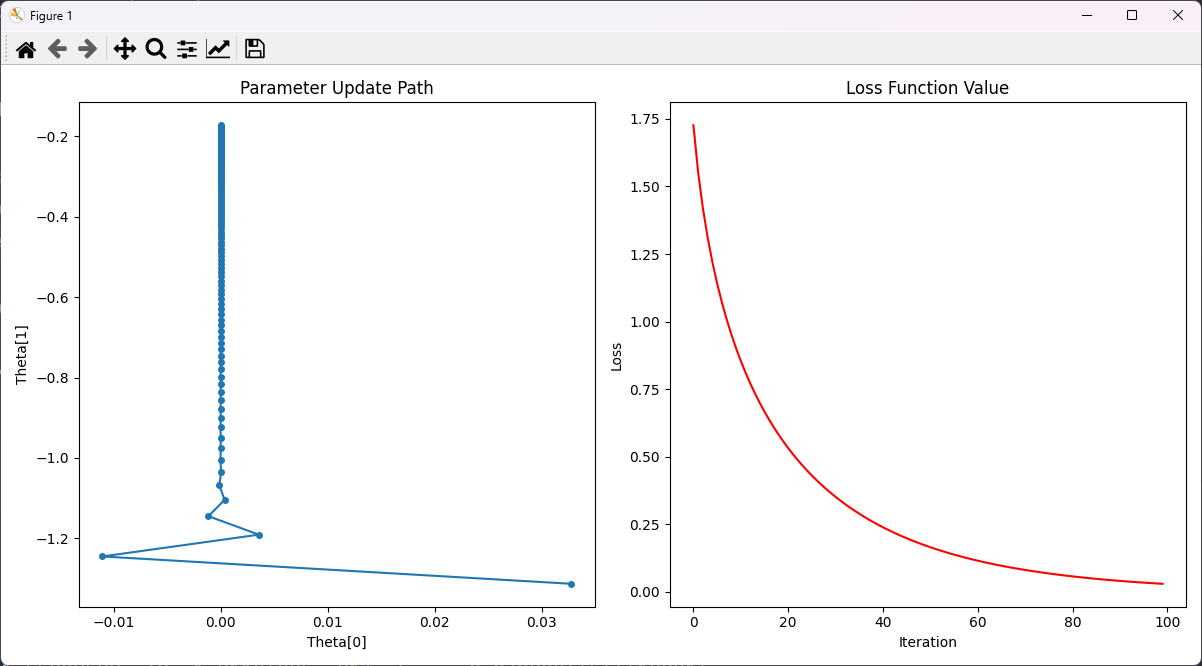
这两个子图展示了AdaGrad算法在优化过程中如何通过自适应调整学习率来更新参数，从而有效地减少损失函数值。
具体来说：

参数更新路径：展示了参数在迭代过程中如何逐渐接近最优值，路径上的点和线条表明参数更新的方向和幅度。
损失函数值：展示了损失值如何随迭代次数减少，反映了模型逐步优化的过程。

AdaGrad 缺点是可能会使得学习率过早、过量的降低，导致模型训练后期学习率太小，较难找到最优解。

5、RMSProp

RMSProp 优化算法是对 AdaGrad 的优化。
最主要的不同是：使用指数移动加权平均梯度替换历史梯度的平方和。

5.1、公式

其计算过程如下：

初始化学习率 $\alpha$ 、初始化参数 $\theta$ 、小常数 $\sigma = 1e-6$
初始化参数 $\theta$
初始化梯度累计变量 $s$
从训练集中采样 $m$ 个样本的小批量，计算梯度 $g$
使用指数移动平均累积历史梯度，公式： $\beta \cdot s + (1 - \beta)g \odot g$
- $\beta$ 是权重系数，控制历史梯度和当前梯度的比例。
- $s$ 是梯度的累积平方和，用于调整学习率。
- $g$ 是当前的梯度， $\odot g$ 表示逐元素平方。

学习率 $\alpha$ 的计算公式： $\alpha = \frac{\alpha}{\sqrt{s + \sigma}}$

这个公式计算的是调整后的学习率。
$\alpha$ 是初始学习率。
$s$ 是累积的梯度平方和。
$\sigma$ 是一个小常数，防止分母为零。

参数更新公式： $\theta = \theta - \frac{\alpha}{\sqrt{s + \sigma}} \cdot g$

这个公式用于更新参数 $\theta$ 。
$\theta$ 是当前的参数值。
$\alpha$ 是初始学习率。
$s$ 是累积的梯度平方和。
$\sigma$ 是一个小常数。
$g$ 是当前的梯度。

这些公式共同作用，通过动态调整学习率来更新参数，使模型逐步逼近最优解。

5.2、代码

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/29 2:30
import numpy as np
import matplotlib.pyplot as plt

# 初始化参数
theta = np.random.randn(2)  # 假设我们有两个参数，随机初始化
alpha = 0.1  # 初始学习率
beta = 0.9  # 指数移动平均的衰减系数
eps = 1e-6  # 防止除零的小常数
s = np.zeros_like(theta)  # 初始化累积梯度平方和


# 定义一个简单的二次损失函数
def loss_function(theta):
    return theta[0] ** 2 + theta[1] ** 2  # 损失函数：J(θ) = θ[0]^2 + θ[1]^2


# 计算梯度
def compute_gradient(theta):
    return 2 * theta  # 梯度：∇J(θ) = [2*θ[0], 2*θ[1]]


# 进行梯度下降迭代
iterations = 100  # 设定迭代次数
theta_history = []  # 存储每次迭代的theta值
loss_history = []  # 存储每次迭代的损失值

for _ in range(iterations):
    gradient = compute_gradient(theta)  # 计算梯度
    s = beta * s + (1 - beta) * (gradient ** 2)  # 更新累积梯度平方和 s = β * s + (1 - β) * g_t ⊙ g_t
    adjusted_alpha = alpha / (np.sqrt(s) + eps)  # 调整学习率 α_t = α / (√s + ε)
    theta -= adjusted_alpha * gradient  # 更新参数 θ = θ - α_t ⊙ g_t

    # 记录参数和损失值以便后续绘图
    theta_history.append(theta.copy())  # 记录当前theta值
    loss_history.append(loss_function(theta))  # 记录当前损失值

    print(f"Updated parameters: {theta}, Loss: {loss_function(theta)}")  # 打印当前参数和损失值

print(f"Optimized parameters: {theta}")  # 打印最终优化后的参数

# 绘制参数更新轨迹
theta_history = np.array(theta_history)  # 将theta历史记录转换为NumPy数组
plt.figure(figsize=(12, 6))  # 创建一个12x6英寸的图形

plt.subplot(1, 2, 1)  # 创建1行2列的子图，选择第一个子图
plt.plot(theta_history[:, 0], theta_history[:, 1], 'o-', markersize=4)  # 绘制theta[0]和theta[1]的变化轨迹
plt.title('Parameter Update Path with RMSProp')  # 设置子图标题
plt.xlabel('Theta[0]')  # 设置x轴标签
plt.ylabel('Theta[1]')  # 设置y轴标签

# 绘制损失函数值变化
plt.subplot(1, 2, 2)  # 选择第二个子图
plt.plot(loss_history, 'r-')  # 绘制损失值变化曲线，红色实线
plt.title('Loss Function Value with RMSProp')  # 设置子图标题
plt.xlabel('Iteration')  # 设置x轴标签
plt.ylabel('Loss')  # 设置y轴标签

plt.tight_layout()  # 自动调整子图布局
plt.show()  # 显示图形

运行：

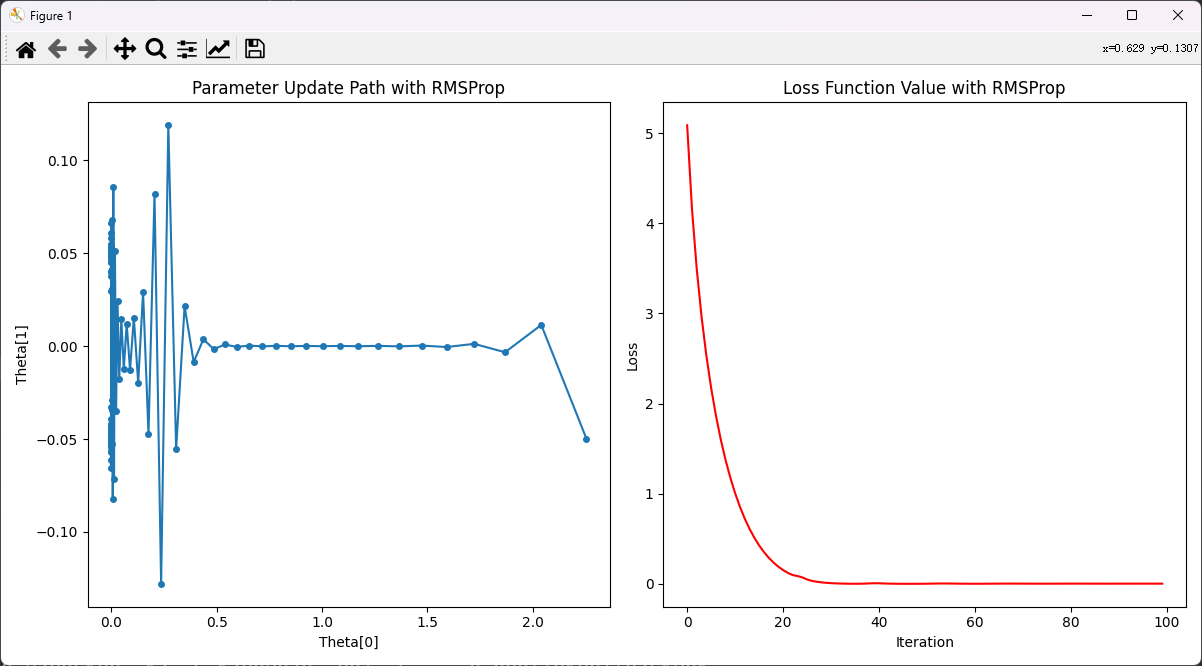
解释：

损失函数值在初始时较高，随着迭代次数的增加，损失值迅速下降。
在前几次迭代中，损失值下降速度非常快，这是因为RMSProp算法在初始阶段调整了每个参数的学习率，使得参数更新步长较大。
随着迭代次数的增加，损失值逐渐趋于平稳，表明模型参数已接近最优值，优化过程收敛。

5.3、小结

RMSProp 与 AdaGrad 最大的区别是对梯度的累积方式不同，对于每个梯度分量仍然使用不同的学习率。
RMSProp 通过引入衰减系数 β，控制历史梯度对历史梯度信息获取的多少。
被证明在神经网络非凸条件下的优化更好，学习率衰减更加合理一些。
需要注意的是：
AdaGrad 和 RMSProp 都是对于不同的参数分量使用不同的学习率，
如果某个参数分量的梯度值较大，则对应的学习率就会较小，
如果某个参数分量的梯度较小，则对应的学习率就会较大一些

6、Adam

Momentum （Adaptive Moment Estimation）使用指数加权平均计算当前的梯度值、AdaGrad、RMSProp 使用自适应的学习率，Adam 结合了 Momentum、RMSProp 的优点，
使用：移动加权平均的梯度和移动加权平均的学习率。
使得能够自适应学习率的同时，也能够使用 Momentum 的优点。

6.1、公式和步骤解释⭐

初始化：
- 学习率 $\alpha$
- 参数 $\theta$
- 一阶动量估计 $m$ 初始化为0
- 二阶动量估计 $v$ 初始化为0
- 小常数 $\epsilon$ ，防止除零错误，通常为 $10^{-8}$
- 一阶动量估计的衰减系数 $\beta_1$ ，通常为0.9
- 二阶动量估计的衰减系数 $\beta_2$ ，通常为0.999
**计算梯度：**从训练集中采样 $m$ 个样本的小批量，计算梯度 $g$
更新一阶动量估计： $m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t$
更新二阶动量估计： $v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2$
计算一阶动量估计的偏差修正： $\hat{m_t} = \frac{m_t}{1 - \beta_1^t}$
计算二阶动量估计的偏差修正： $\hat{v_t} = \frac{v_t}{1 - \beta_2^t}$
更新参数： $\theta = \theta - \alpha \frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon}$
重复步骤2-7，直到满足停止条件（如迭代次数或误差足够小）

解释：

一阶动量估计 $m_t$ ：
- $m_t$ 是梯度的指数加权平均。
- $\beta_1$ 是动量项的衰减率，接近1时动量项的影响较大。
二阶动量估计 $v_t$ ：
- $v_t$ 是梯度平方的指数加权平均。
- $\beta_2$ 是RMSProp中的衰减率，控制过去梯度平方的影响。
偏差修正：
- 由于 $m_t$ 和 $v_t$ 在初始化时为0，前几步的估计值会有偏差。通过除以 $\beta_1^t)$ 和 $\beta_2^t)$ 对其进行修正。
参数更新：
- 使用修正后的动量估计和梯度平方估计更新参数。
- $\epsilon$ 防止分母为零，提高数值稳定性。

这些步骤确保了Adam优化算法能够快速收敛，并且在不同问题和数据集上表现良好。

6.2、代码⭐

# -*- coding: utf-8 -*-
# @Author: CSDN@逐梦苍穹
# @Time: 2024/7/29 2:43
import numpy as np
import matplotlib.pyplot as plt

# 初始化参数
theta = np.random.randn(2)  # 假设我们有两个参数，随机初始化
alpha = 0.1  # 初始学习率
beta1 = 0.9  # 一阶动量估计的衰减系数
beta2 = 0.999  # 二阶动量估计的衰减系数
eps = 1e-8  # 防止除零的小常数
m = np.zeros_like(theta)  # 初始化一阶动量估计
v = np.zeros_like(theta)  # 初始化二阶动量估计


# 定义一个简单的二次损失函数
def loss_function(theta):
    return theta[0] ** 2 + theta[1] ** 2  # 损失函数：J(θ) = θ[0]^2 + θ[1]^2


# 计算梯度
def compute_gradient(theta):
    return 2 * theta  # 梯度：∇J(θ) = [2*θ[0], 2*θ[1]]


# 进行梯度下降迭代
iterations = 100  # 设定迭代次数
theta_history = []  # 存储每次迭代的theta值
loss_history = []  # 存储每次迭代的损失值

for t in range(1, iterations + 1):
    gradient = compute_gradient(theta)  # 计算梯度
    m = beta1 * m + (1 - beta1) * gradient  # 更新一阶动量估计 m_t = β1 * m_{t-1} + (1 - β1) * g_t
    v = beta2 * v + (1 - beta2) * (gradient ** 2)  # 更新二阶动量估计 v_t = β2 * v_{t-1} + (1 - β2) * g_t^2
    m_hat = m / (1 - beta1 ** t)  # 计算一阶动量估计的偏差修正 m_hat_t = m_t / (1 - β1^t)
    v_hat = v / (1 - beta2 ** t)  # 计算二阶动量估计的偏差修正 v_hat_t = v_t / (1 - β2^t)
    theta -= alpha * m_hat / (np.sqrt(v_hat) + eps)  # 更新参数 θ = θ - α * m_hat_t / (√v_hat_t + ε)

    # 记录参数和损失值以便后续绘图
    theta_history.append(theta.copy())  # 记录当前theta值
    loss_history.append(loss_function(theta))  # 记录当前损失值

    print(f"Updated parameters: {theta}, Loss: {loss_function(theta)}")  # 打印当前参数和损失值

print(f"Optimized parameters: {theta}")  # 打印最终优化后的参数

# 绘制参数更新轨迹
theta_history = np.array(theta_history)  # 将theta历史记录转换为NumPy数组
plt.figure(figsize=(12, 6))  # 创建一个12x6英寸的图形

plt.subplot(1, 2, 1)  # 创建1行2列的子图，选择第一个子图
plt.plot(theta_history[:, 0], theta_history[:, 1], 'o-', markersize=4)  # 绘制theta[0]和theta[1]的变化轨迹
plt.title('Parameter Update Path with Adam')  # 设置子图标题
plt.xlabel('Theta[0]')  # 设置x轴标签
plt.ylabel('Theta[1]')  # 设置y轴标签

# 绘制损失函数值变化
plt.subplot(1, 2, 2)  # 选择第二个子图
plt.plot(loss_history, 'r-')  # 绘制损失值变化曲线，红色实线
plt.title('Loss Function Value with Adam')  # 设置子图标题
plt.xlabel('Iteration')  # 设置x轴标签
plt.ylabel('Loss')  # 设置y轴标签

plt.tight_layout()  # 自动调整子图布局
plt.show()  # 显示图形

结果：

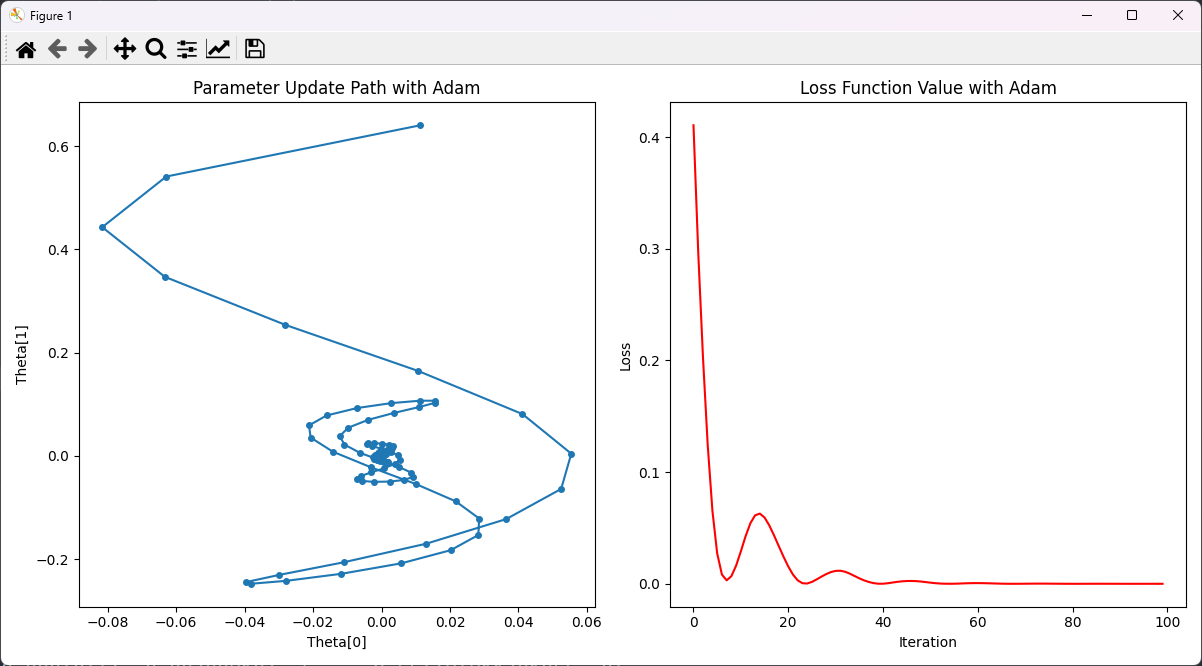
解释：

损失函数值在初始时较高，随着迭代次数的增加，损失值迅速下降。
在前几次迭代中，损失值下降速度非常快，这是因为Adam算法在初期阶段通过一阶和二阶动量的结合，使得参数更新步长较大。
随着迭代次数的增加，损失值逐渐趋于平稳，表明模型参数已接近最优值，优化过程收敛。
中间出现了几次小的波动，这可能是由于参数在接近局部最优值时调整的结果，但总体趋势是下降的。

6.3、优点

自适应学习率：Adam通过计算每个参数的自适应学习率，使得算法在训练过程中更加稳定。
动量加速：Adam使用动量估计（Momentum）来加速梯度下降，提高收敛速度。
偏差校正：Adam对一阶和二阶动量估计进行偏差校正，使得估计值更加准确。
适用于大规模数据和高维参数：Adam在处理大规模数据和高维参数时表现出色，特别适用于神经网络和深度学习模型的训练。
鲁棒性强：Adam对超参数的选择不敏感，通常默认的超参数设置（如 β1=0.9\beta_1 = 0.9β1=0.9，β2=0.999\beta_2 = 0.999β2=0.999）在多数情况下表现良好。

7、何为鞍点

这张图展示了一个典型的鞍点。鞍点在图的中心区域，表面在X轴方向上呈现凹陷，在Y轴方向上呈现上升，形成了一个鞍形。图中的蓝色箭头表示梯度下降的路径，可以看到这些路径在鞍点附近变慢和弯曲，表明梯度在鞍点处非常小，使得优化过程在该区域变得缓慢和不稳定。

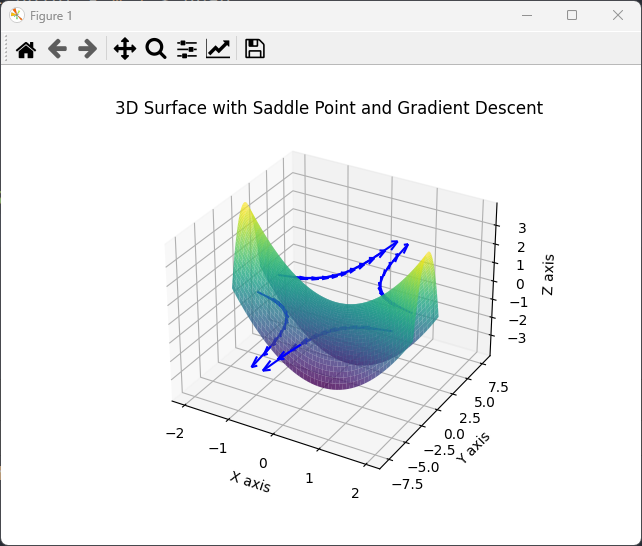
代码：

import numpy as np
import matplotlib.pyplot as plt

# 创建网格
x = np.linspace(-2, 2, 400)  # 在-2到2之间生成400个等距点
y = np.linspace(-2, 2, 400)  # 在-2到2之间生成400个等距点
X, Y = np.meshgrid(x, y)  # 生成网格点
Z = X**2 - Y**2  # 定义鞍点函数 Z = X^2 - Y^2

# 绘制3D表面图
fig = plt.figure()  # 创建一个新图形
ax = fig.add_subplot(111, projection='3d')  # 添加一个3D子图
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)  # 绘制3D表面，使用'viridis'颜色映射，透明度为0.8

# 定义一个函数来绘制箭头表示梯度下降路径
def plot_arrow(ax, start, direction, length=0.2, color='r'):
    ax.quiver(start[0], start[1], start[2],  # 箭头起点
              direction[0], direction[1], direction[2],  # 箭头方向
              color=color, length=length, arrow_length_ratio=0.3)  # 颜色、长度和箭头长度比例

# 梯度下降路径
start_points = [(-1.5, 1.5), (1.5, -1.5), (-1.5, -1.5), (1.5, 1.5)]  # 定义四个起始点
for x0, y0 in start_points:  # 遍历每个起始点
    point = np.array([x0, y0, x0**2 - y0**2])  # 计算起始点的初始位置
    for _ in range(10):  # 模拟梯度下降的迭代
        grad = np.array([2*point[0], -2*point[1], 0])  # 计算当前梯度
        plot_arrow(ax, point, -grad, color='blue')  # 绘制梯度下降路径的箭头
        point = point - 0.1 * grad  # 更新点位置，步长为0.1

# 设置轴标签和标题
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_zlabel('Z axis')
ax.set_title('3D Surface with Saddle Point and Gradient Descent')

# 显示图像
plt.show()  # 显示绘制的图形

8、小结

介绍常见的一些对普通梯度下降算法的优化方法，主要有 Momentum、AdaGrad、RMSProp、Adam 等优化方法。
其中 Momentum 使用指数加权平均参考了历史梯度，使得梯度值的变化更加平缓；
AdaGrad 则是针对学习率进行了自适应优化，由于其实现可能会导致学习率下降过快，RMSProp 对 AdaGrad 的学习率自适应计算方法进行了优化；
Adam 则是综合了 Momentum 和 RMSProp 的优点，在很多场景下，Adam 的表示都很不错
选择标准：