文章目录
- 1. 概述
- 2. 参数定义
- 3. CNN 网络
1. 概述
– 1. 卷积神经网络 CNNs
– 2. 连续型线性分段函数 F
– 3. 损失函数
– 4. 链式法则计算反向传播算法梯度
∇
F
=
g
r
a
d
F
\nabla F= \mathrm{grad}\; F
∇F=gradF
2. 参数定义
- 我们定义每个样本有m维度特征,有n个样本;具体如下
X = [ x 1 x 2 ⋯ x n ] , x i = [ x i 1 x i 2 ⋮ x i m ] \begin{equation} X=\begin{bmatrix}x_1&x_2&\cdots&x_n\end{bmatrix},x_i=\begin{bmatrix}x_{i1}\\\\x_{i2}\\\\\vdots\\\\x_{im}\end{bmatrix}\end{equation} X=[x1x2⋯xn],xi= xi1xi2⋮xim - 最终问题为
二分类问题,创建一个神经网络函数 F ( x ) F(x) F(x)如下:
R e s u l t = { + 1 F ( X ) > 0 − 1 F ( X ) < 0 \begin{equation} Result=\left\{ \begin{aligned} +1&&F(X)>0 \\ -1&&F(X)<0 \\ \end{aligned} \right. \end{equation} Result={+1−1F(X)>0F(X)<0 - 有趣的可视化训练神经网络网站 TensorFlow
- 激活函数,也叫非线性函数,是为了将线性函数转换为非线性函数,提高模型拟合能力
R e L u ( x ) = max { 0 , x } \begin{equation} \mathrm{ReLu}(x)=\max\{0,x\} \end{equation} ReLu(x)=max{0,x}

- Epoch(一代训练) :使用训练集的全部数据对模型进行一次完整训练为
一代训练 - Batch(一批数据):使用训练集中的一小部分样本对模型权重进行一次反向传播的参数更新,这一部分样本被称为
一批数据 - Iteration(一次迭代):使用一个Batch数据对模型继续宁一次参数更i性能的过程叫做
一次迭代
3. CNN 网络
y
1
=
A
1
x
0
+
b
;
y
1
→
6
×
1
;
A
1
→
4
×
3
;
x
0
→
3
×
1
;
b
→
4
×
1
\begin{equation} y_1=A_1x_0+b;y_1\to 6\times 1;A_1\to 4\times 3;x_0 \to 3\times 1; b\to 4\times 1 \end{equation}
y1=A1x0+b;y1→6×1;A1→4×3;x0→3×1;b→4×1

- 单个神经元函数如下:
F 1 ( x ) = R e L u ( A 1 x 0 + b 1 ) \begin{equation} F_1(x)=\mathrm{ReLu}(A_1x_0+b_1) \end{equation} F1(x)=ReLu(A1x0+b1) - 多层网络函数表示如下:
F ( x ) = F 3 ( F 2 ( F 1 ( x ) ) ) \begin{equation} F(x)=F_3(F_2(F_1(x))) \end{equation} F(x)=F3(F2(F1(x))) - 那么可以简单的把
F
(
X
)
F(X)
F(X)看作是一个分段线性函数:简单来说,卷积神经网络函数还是用一系列分段的线段来拟合复杂的函数,

- 超平面切割

- 计算公式
- 特例,当m为2时:
r ( N , 2 ) = C N 0 + C N 1 + C N 2 \begin{equation} r(N,2)=C_N^0+C_N^1+C_N^2 \end{equation} r(N,2)=CN0+CN1+CN2
 - 递归公式:
- 递归公式:



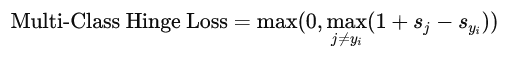









![[Meachines] [Easy] Blocky Jar包反编译](https://img-blog.csdnimg.cn/img_convert/818744d5ae408aec3e4b400cd53fe857.jpeg)