[论文笔记]一种超越思维链的提示策略—

引言

今天带来另一种提示策略论文笔记：LEAST-TO-MOST PROMPTING ENABLES COMPLEX REASONING IN LARGE LANGUAGE MODELS。

思维链提示在各种自然语言推理任务中表现出了显著的性能。然而，在需要解决比提示中示例更难的问题时，它的表现往往较差。为了克服这种从简单到困难的泛化挑战，作者提出了一种新颖的提示策略——从最少到最多提示(least-to-most prompting)。

这种策略的关键思想是将复杂问题分解为一系列较简单的子问题，然后按顺序解决它们。每个子问题的解决都依赖于之前已解决子问题的答案。

1. 总体介绍

尽管深度学习在过去十年取得了巨大成功，但人类智能与机器学习之间仍然存在巨大差异：(1)面对新任务，人了通常只需要少量示例就能学习完成任务，而机器学习需要大量标注数据进行训练；(2)人类能清晰地解释其预测或决策背后的基本原理，而机器学习本质上是一个黑盒；(3)人类能够解决比他们之前见过的任何问题都要更加困难的问题，而对于机器学习，训练和测试中的样本通常是相同难度水平。

最近提出的思维链方法在缩小人类智能和机器智能之间迈出了重要一步。然而，思维链提示存在一个关键限制——在需要比示例更难的问题上进行泛化的表现往往不佳。为了解决这种从简单到困难的泛化问题，作者提出了少到多提示(least-to-most prompting)。

该方法分为两个阶段：首先将复杂问题分解为一系列更简单的问题，然后按顺序解决这些子问题。其中解决给定子问题的过程中可以参考之前解决的子问题的答案。这两个阶段都是通过少样本来实现的，不涉及训练和微调。图1展示了该方法。

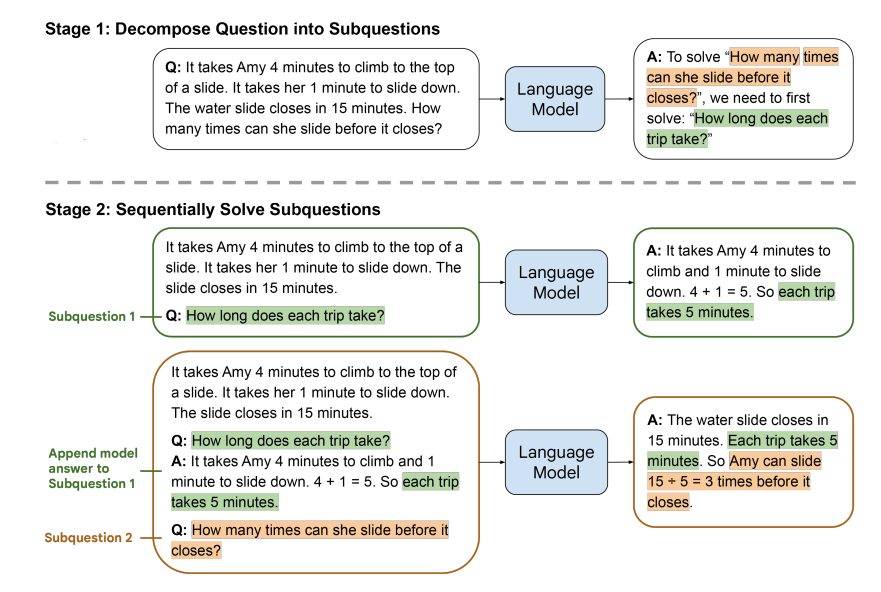
图1：从少到多提示的两阶段解决数学问题：(1) 查询语言模型以将问题分解为子问题；(2) 查询语言模型按顺序解决子问题。第二个子问题的答案基于第一个子问题的答案。

2. 少到多提示

少到多提示通过将复杂问题分解为一系列更简单的子问题，教会语言模型如何解决复杂问题。它由两个顺序阶段组成：

分解。这一阶段的提示包含展示如何分解的固定示例，随后是要被分解的具体问题。
子问题求解。这一阶段的提示由三个部分组成：(1) 展示如何解决子问题的固定示例；(2) 先前回答的子问题和生成的解决方案(可能为空列表)；(3) 下一个需回答的问题。

在图1中所示的例子中，首先要求语言模型将原始问题分解为子问题。传递给模型的提示包含示例，说明如何分解复杂问题（这些示例在图中未显示），随后是要被分解的具体问题（如图所示）。语言模型得出结论，原始问题可以通过解决一个中间问题"每次旅行需要多长时间？"来解决。

在下一个阶段，要求语言模型按顺序解决从问题分解阶段得到的子问题。原始问题作为最后一个子问题附加在后面。求解从向语言模型传递一个包含展示如何解决问题的示例的提示开始（未在图中显示），接着是第一个子问题"每次旅行需要多长时间？"。然后，取出语言模型生成的答案(…每次旅行需要5分钟。)，通过将生成的答案附加到之前的提示中，构建下一个提示，随后是下一个子问题，恰好在此例中是原始问题。新的提示随后被传回给语言模型，模型返回最终答案。

少到多提示可以与其他提示技术结合，例如思维链和自一致性，但并不一定需要。

3. 结果

展示了从少到多提示在符号操作、组合泛化和数学推理任务中的结果，并将其与思维链提示进行了比较。

3.1 符号操作

以最后字母连接任务为例。在该任务中，每个输入是一组单词，对应的输出是该列表中单词最后字母的连接。例如，thinking, machine的输出是ge，因为thinking的最后一个字母是g，machine的最后一个字母是e。

当测试列表的长度与提示示例中的列表长度相同时，思维链提示表现得非常出色。然而，当测试列表的长度远大于提示示例中的列表时，其表现较差。而少到多提示克服了这一限制，并在长度泛化上显著超越了思维链提示。

少到多提示 少到多提示上下文显示在表1和表2中。表1中的示例演示了如何将列表分解为一系列子列表。表2中的示例则演示了如何将输入映射到期望的输出。表2中的示例则演示了如何将输入映射到期望的输出。给定一个新列表，首先将其附加到表1中的示例，以构建分解提示，然后将其发送到语言模型以获取该列表的分解结果。接下来，为每个子列表 $S$ 构建一个解决提示，该提示由表2中的示例组成，后跟之前的子列表/响应对(如果有的话)，再接 $S$ 。依次向语言模型发出这些提示，并将最后的响应作为最终解决方案。

链式思维提示 该任务的思维链提示上下文列在表3中。它使用与表2中少到多提示相同的列表。唯一的区别在于，在思维链提示中，针对第二个列表think, machine, learning的响应是从头开始构建的，而不是使用第一个列表hink, machine的输出。

将少到多提示(表1和表2)与链式思维提示(表3)以及标准的少样本提示进行比较。标准少样本提示的构造方式是去掉思维链提示中的中间解释。也就是说，它仅由这两个示例组成：(1)think, machine的输出是 ke；(2) think, machine, learning的输出是 keg。

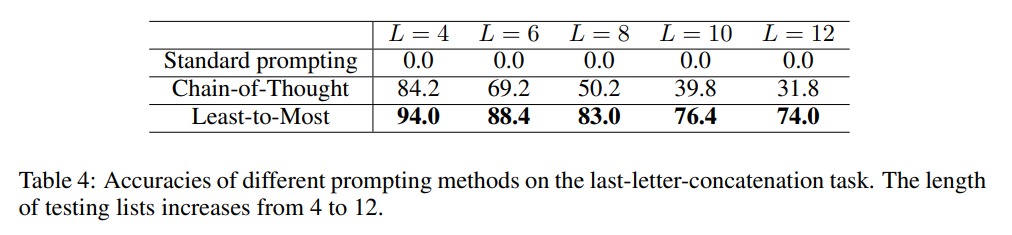
结果不同方法在GPT-3中使用code-davinci-002的准确率如表4所示。标准少样本提示在所有测试案例中完全失败，准确率为0。思维链提示相较于标准提示显著提升了性能，但仍远远落后于少到多提示，特别是在列表较长时。此外，随着列表长度的增加，思维链提示的性能下降速度比少到多提示要快得多。

错误分析 尽管少到多提示的表现显著优于思维链提示，但对于长列表而言，准确率仍远未达到100%。作者发现，只有极少部分错误是由于最后字母不正确造成的，而大多数错误则是连接错误(丢失或添加字母)。

3.2 组合泛化

SCAN可能是评估组合泛化最流行的基准测试。它要求将自然语言命令映射到动作序列(见表5)。在长度拆分的情况下，序列到序列模型的表现很差，因为训练集中的动作序列要短于测试集中的动作序列。

使用少到多提示的大型语言模型可以仅通过少量示例来解决SCAN，不需要任何训练或微调。

少到多提示 SCAN的少到多提示基于两种类型的提示：(1)命令分解提示，其中包含8个示例，用以展示如何将一个长命令分解为一系列短命令；(2)命令映射提示，其中包含14个示例，用以展示如何将自然语言命令映射到动作序列。

分解的提示上下文如下：

# 命令映射。命令映射提示上下文由一组命令组成，以及相应的动作序列和它们是如何获得的解释。

Q: "turn left"  
A: "turn left" 输出 "TURN LEFT"。  

Q: "turn right"  
A: "turn right" 输出 "TURN RIGHT"。  

Q: "jump left"  
A: "jump left" 的输出拼接： "turn left" 的输出，"jump" 的输出。 "turn left" 输出 "TURN LEFT"。 "jump" 输出 "JUMP"。所以，“turn left”和“jump”的输出拼接结果为 "TURN LEFT" + "JUMP"。因此，"jump left" 的输出为 "TURN LEFT" + "JUMP"。  

Q: "run right"  
A: "run right" 的输出拼接： "turn right" 的输出，"run" 的输出。 "turn right" 输出 "TURN RIGHT"。 "run" 输出 "RUN"。所以，“turn right”和“run”的输出拼接结果为 "TURN RIGHT" + "RUN"。因此，"run right" 的输出为 "TURN RIGHT" + "RUN"。  

Q: "look twice"  
A: "look twice" 的输出拼接： "look" 的输出，"look" 的输出。 "look" 输出 "LOOK"。所以，重复 "look" 的输出两次的结果为 "LOOK" * 2。因此，"look twice" 的输出为 "LOOK" * 2。  

Q: "run and look twice"  
A: "run and look twice" 的输出拼接： "run" 的输出，"look twice" 的输出。 "run" 输出 "RUN"。 "look twice" 输出 "LOOK" * 2。所以，“run”和“look twice”的输出拼接结果为 "RUN" + "LOOK" * 2。因此，"run and look twice" 的输出为 "RUN" + "LOOK" * 2。  

Q: "jump right thrice"  
A: "jump right thrice" 的输出拼接： "jump right" 的输出，"jump right" 的输出，"jump right" 的输出。 "jump right" 输出 "TURN RIGHT" + "JUMP"。所以，重复 "jump right" 的输出三次的结果为 ("TURN RIGHT" + "JUMP") * 3。因此，"jump right thrice" 的输出为 ("TURN RIGHT" + "JUMP") * 3。  

Q: "walk after run"  
A: "walk after run" 的输出拼接： "run" 的输出，"walk" 的输出。 "run" 输出 "RUN"。 "walk" 输出 "WALK"。所以，“run”和“walk”的输出拼接结果为 "RUN" + "WALK"。因此，"walk after run" 的输出为 "RUN" + "WALK"。  

Q: "turn opposite left"  
A: "turn opposite left" 的输出拼接： "turn left" 的输出，"turn left" 的输出。 "turn left" 输出 "TURN LEFT"。所以，重复 "turn left" 的输出两次的结果为 "TURN LEFT" * 2。因此，"turn opposite left" 的输出为 "TURN LEFT" * 2。  

Q: "turn around left"  
A: "turn around left" 的输出拼接： "turn left" 的输出，"turn left" 的输出，"turn left" 的输出，"turn left" 的输出。 "turn left" 输出 "TURN LEFT"。所以，重复 "turn left" 的输出四次的结果为 "TURN LEFT" * 4。因此，"turn around left" 的输出为 "TURN LEFT" * 4。  

Q: "turn opposite right"  
A: "turn opposite right" 的输出拼接： "turn right" 的输出，"turn right" 的输出。 "turn right" 输出 "TURN RIGHT"。所以，重复 "turn right" 的输出两次的结果为 "TURN RIGHT" * 2。因此，"turn opposite right" 的输出为 "TURN RIGHT" * 2。  

Q: "turn around right"  
A: "turn around right" 的输出拼接： "turn right" 的输出，"turn right" 的输出，"turn right" 的输出，"turn right" 的输出。 "turn right" 输出 "TURN RIGHT"。所以，重复 "turn right" 的输出四次的结果为 "TURN RIGHT" * 4。因此，"turn around right" 的输出为 "TURN RIGHT" * 4。  

Q: "walk opposite left"  
A: "walk opposite left" 的输出拼接： "turn opposite left" 的输出，"walk" 的输出。 "turn opposite left" 输出 "TURN LEFT" * 2。 "walk" 输出 "WALK"。所以，“turn opposite left”和“walk”的输出拼接结果为 "TURN LEFT" * 2 + "WALK"。因此，"walk opposite left" 的输出为 "TURN LEFT" * 2 + "WALK"。  

Q: "walk around left"  
A: "walk around left" 的输出拼接： "walk left" 的输出，"walk left" 的输出，"walk left" 的输出，"walk left" 的输出。 "walk left" 输出 "TURN LEFT" + "WALK"。所以，重复 "walk around left" 的输出四次的结果为 ("TURN LEFT" + "WALK") * 4。因此，"walk around left" 的输出为 ("TURN LEFT" + "WALK") * 4。

映射的提示上下文如下：

#命令分解。命令分解提示上下文由一组#命令及其相应的分解命令序列组成。
Q: "look right after look twice"
A: "look right after look twice" 可以通过以下方式解决： "look right", "look twice"。
Q: "jump opposite right thrice and walk"
A: "jump opposite right thrice" 可以通过以下方式解决： "jump opposite right", "jump opposite right thrice"。 "walk" 可以通过以下方式解决： "walk"。所以，"jump opposite right thrice and walk" 可以通过以下方式解决： "jump opposite right", "jump opposite right thrice", "walk"。
Q: "run left twice and run right"
A: "run left twice" 可以通过以下方式解决： "run left", "run left twice"。 "run right" 可以通过以下方式解决： "run right"。所以，"run left twice and run right" 可以通过以下方式解决： "run left", "run left twice", "run right"。
Q: "run opposite right"
A: "run opposite right" 可以通过以下方式解决： "run opposite right"。
Q: "look opposite right thrice after walk"
A: "look opposite right thrice" 可以通过以下方式解决： "look opposite right", "look opposite right thrice"。 "walk" 可以通过以下方式解决： "walk"。所以，"look opposite right thrice after walk" 可以通过以下方式解决： "look opposite right", "look opposite right thrice", "walk"。
Q: "jump around right"
A: "jump around right" 可以通过以下方式解决： "jump right", "jump around right"。所以，"jump around right" 可以通过以下方式解决： "jump right", "jump around right"。
Q: "look around right thrice and walk"
A: "look around right thrice" 可以通过以下方式解决： "look right", "look around right", "look around right thrice"。 "walk" 可以通过以下方式解决： "walk"。所以，"look around right thrice and walk" 可以通过以下方式解决： "look right", "look around right", "look around right thrice", "walk"。
Q: "turn right after run right thrice"
A: "turn right" 可以通过以下方式解决： "turn right"。 "run right thrice" 可以通过以下方式解决： "run right", "run right thrice"。所以，"turn right after run right thrice" 可以通过以下方式解决： "turn right", "run right", "run right thrice"。

使用Python表示法来制定提示，以实现从少到多的提示方式。例如，在提示设计中，将look twice映射为"LOOK" * 2，而不是"LOOK LOOK"。

思维链提示 SCAN的思维链提示使用与少到多提示相同的命令映射上下文(表7)，但不使用命令分解。

结果将少到多的提示与思维链提示和标准少样本提示进行比较。不同提示方法在不同语言模型下的准确率见表8。使用code-davinci-002，少到多的提示在长度拆分下的准确率达到99.7%。此外，无论提示方法如何，code-davinci-002始终优于text-davinci-002。

错误分析 在长度拆分的测试集中，少到多提示总共有13次失败：其中6次错误地将twice和thrice理解为跟随around，其余的错误地将after理解为and。

3.3 数学推理

应用从少到多的提示来解决GSM8K和DROP中的数学文字问题。观察大型语言模型结合少到多的提示是否能够解决比提示中更困难的问题。在这里，简单地通过解决步骤的数量来衡量问题的难度。设计的用于解决GSM8K的提示如表9所示。示例由两个部分组成。第一部分(从Let's break down this problem开始）展示了如何将原始问题分解为更简单的子问题，而第二部分展示了如何按顺序解决这些子问题。

这个提示将分解和子问题解决结合为一个过程。也可以分别为分解和子问题解决设计两个不同的提示。

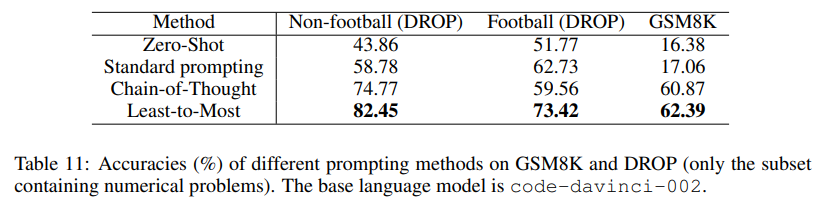
还构建了一个思维链提示(表10)作为基线。它是通过移除分解部分而少到多提示(表9)派生的。结果如表11所示。总体而言，少到多的提示仅略微改善了思维链提示。然而，针对需要至少5个步骤才能解决的问题，少到多的提示基本上提升了思维链提示的表现。

对于DROP基准测试，少到多的提示以较大幅度超越了思维链提示(表11)。这可能是因为DROP中的大多数问题可以被简单地分解。

4. 相关工作

组合泛化 SCAN是评估组合泛化的广泛使用的基准。在所有的拆分中，最具挑战性的是长度拆分，这要求模型能够推广到比训练序列更长的测试序列。之前在SCAN上表现良好的工作大多提出了神经-符号架构和语法归纳技术。与现有工作不同的是，作者展示了在没有特别设计用于改善组合泛化的模型架构和符号组件的情况下，少到多的提示在任何拆分上取得了99.7%的准确率，并且只需要少量的示例，不需要任何训练或微调。

易到难泛化 除了组合泛化之外，还有许多其他任务，其中测试用例需要比训练示例更多的推理步骤才能解决。Dong等人提出了神经逻辑机用于归纳学习和逻辑推理。Schwarzschild等人表明，对简单问题进行少量重复步骤训练的循环网络可以通过在推理过程中执行额外的重复步骤来解决更复杂的问题。在作者的方法中，通过将复杂问题分解为一系列较简单的问题，实现了易到难的泛化。

任务分解 Perez等人将一个多跳问题分解为多个独立的单跳子问题，这些子问题可以由现成的问答模型回答。然后将这些答案进行聚合以形成最终答案。问题分解和答案聚合都是由经过训练的模型实现的。Wang等人通过将提示建模为连续的虚拟标记，并通过迭代提示从语言模型中引出相关知识，来进行多跳问答。与这些方法不同的是，作者的方法不涉及任何训练或微调。此外，在少到多提示的过程中生成的子问题通常是相关的，并且必须按特定顺序顺序解决，以便某些子问题的答案可以用作解决其他子问题的构建模块。

5. 限制

通常情况下，分解提示在不同领域之间的泛化效果不好。例如，一个展示了分解数学词问题的提示，对于教授大型语言模型分解常识推理问题并不有效。必须设计一个新的提示来展示这些类型问题的分解，以实现最佳性能。

即使在同一个领域内，泛化分解也可能很困难。几乎所有GSM8K中的问题，如果大型语言模型能够获得这些具有挑战性问题的正确分解，那么这些问题都可以被准确解决。这个发现并不令人惊讶，并且与我们在解决数学问题时的经验相一致。每当我们成功地将一个数学问题分解为可以解决的更简单的子问题时，我们本质上解决了原始问题。

在最后一个字母连接任务和SCAN基准测试中取得了出色的结果，因为在这些任务中，分解相对直接简单。