1.卷积的意义
1.1从LTI的角度看
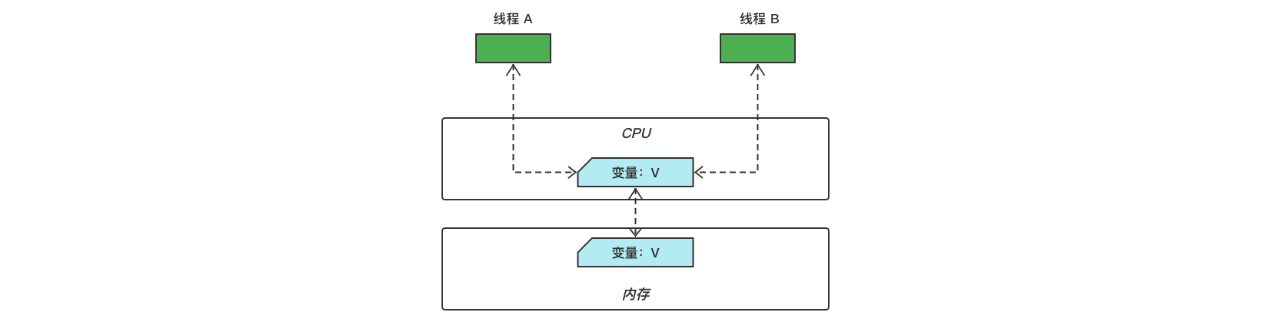
卷积最开始其实是信号处理中用来描述线性移不变系统Linear time-invariant systems的。线性,表明可以叠加,信号可以拆分成脉冲的响应;时不变,指信号不随着时间的迁移改变,意味着能量守恒。
那么,由线性时不变的性质,可以把输入信号拆成一个个的脉冲信号:

然后再由时不变的性质,每个冲激处的响应都是一样的:

那么当求t3时刻的输出信号时,利用线性的性质,输出值就是三个响应(上图红色点)的叠加。
![]() 这时再看表达式就清楚一些了:
这时再看表达式就清楚一些了:
1. x[k]的本质是权重系数,是输入信号拆分后每个位置的冲激;
2. 系统响应h原本在t=0的位置,被冲激向右移动距离k到达一个新的位置,然后取此时n位置的响应h[n-k];
3.响应和在x[k]下加权求和,得到输出信号。
4.虽然公式中是对正负无穷的冲激进行求和,但是t之后的响应其实不会对t时刻造成影响的。
5.时域的卷积等效于频域相乘,所以卷积也被称作滤波。
1.2从积分的角度看
![]()
既然是加权求和,在连续的情况下就是积分,积分的对象是两个函数的乘积。x[k]保持不变,h[k]先进行左右对称翻转,得到h[-k],然后再右移k,得到h[n-k]。参考维基百科,有下面的图示:
这样的解释从几何上看更加直观地表示公式本身,但其实也更难以理解为什么要“翻转”。但好处是可以直观地对比与互相关的不同:

互相关没有翻转,所以当卷积符号右边的函数是对称函数时,卷积等价于互相关。
2. 二维卷积
对大部分人来说,图像中的二维卷积是更为熟悉的。它其实和一维卷积一样,仍然是翻转,滑动和加权。只不过一般性的卷积都是对称的,所以就等价于求相关。这也是为什么之前说到的拉普拉斯算子可以求斑点,因为拉普拉斯算子本身的响应就是一个墨西哥草帽的样式。
结合LTI的性质,二维卷积的滤波器就是一个冲激的响应,这个响应是平移不变的,所以才需要那么多滤波器,每个滤波器表示一种响应/特征提取,CNN才“变宽”。
在torch中一般使用torch.nn.Conv2d实现卷积。但这个函数只指定了输入输出的通道数,滤波器的尺寸,步长,填充方式等。输出的尺寸需要下面公式来计算:
上式中的1表示卷积核在初始的左上角位置一定会对应一个输出,第二项表示每移动一次对应一个输出。
填充的方式有Arbitrary padding,Half padding,Full padding。
| No Padding | Half(Same) Padding | Full Padding |
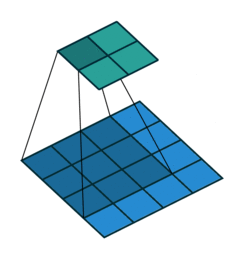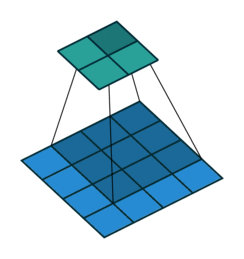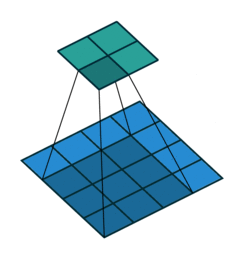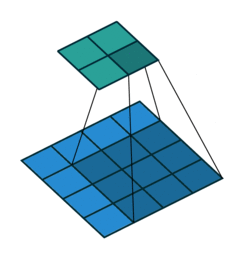 | 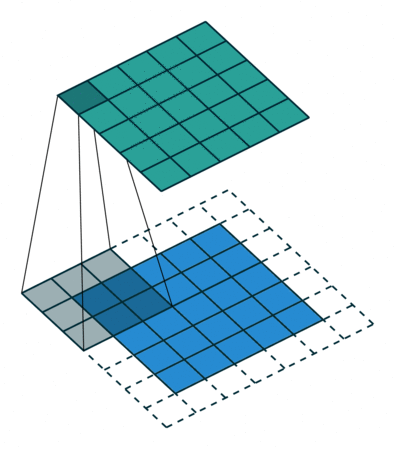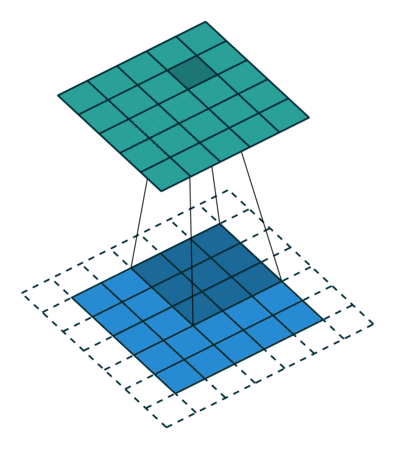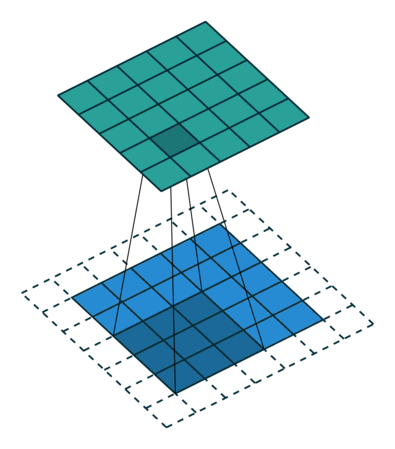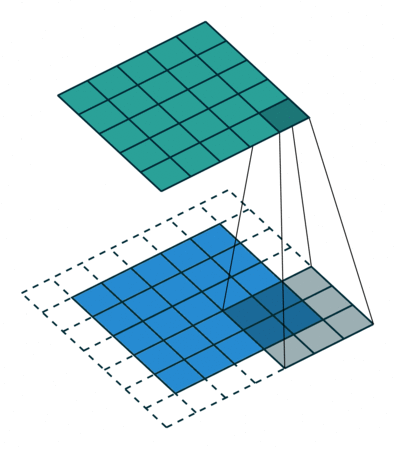 | 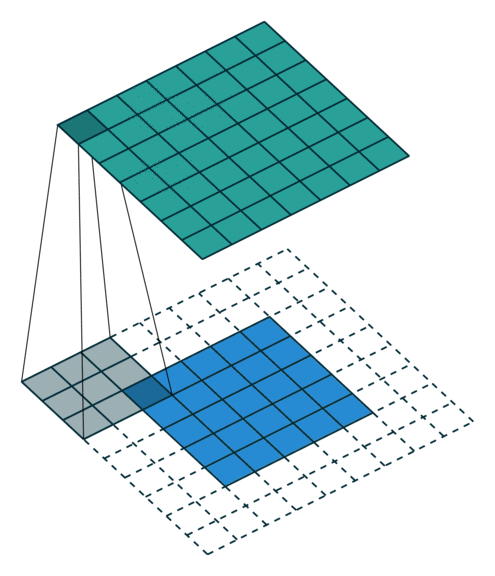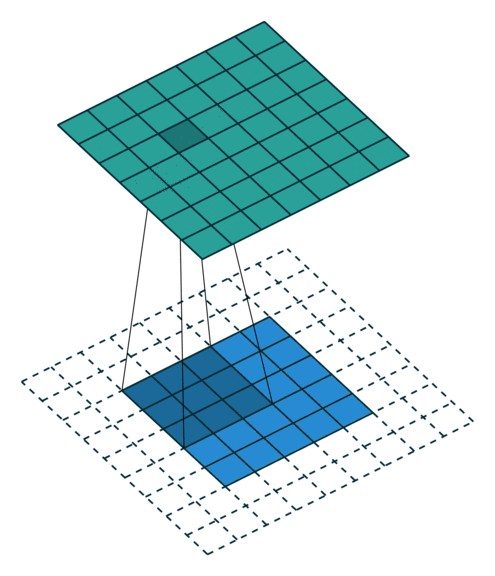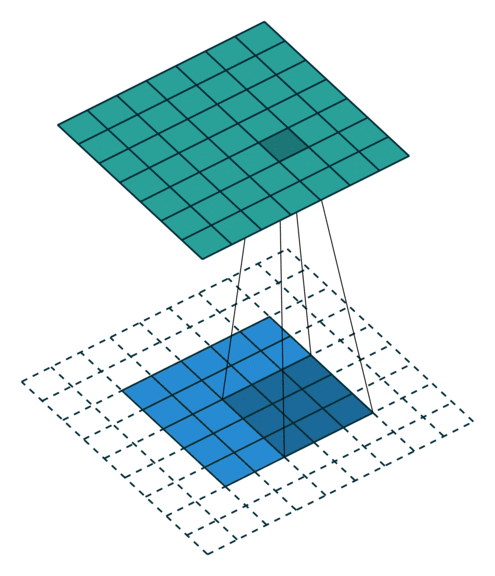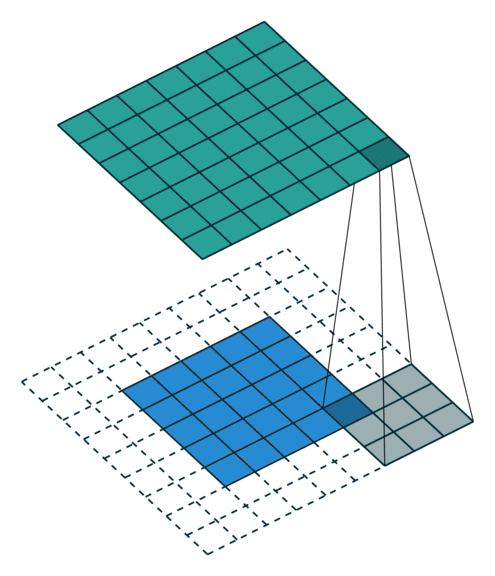 |
| tf的padding有两个值,一个是SAME,一个是VALID valid其实就是不填充? | Half padding第一次卷积的卷积核中心对应填充前的左上角,填充的范围差不多是卷积核尺寸的一半;保证输入和输出的feature map尺寸相同,p=⌊k/2⌋。 | Full padding填充前的左上角则对应卷积核的左下角,填充范围差不多是整个卷积核。如果padding再多,原始的信息没有参与计算,所以这种padding已经是上限了k-1了,所以叫full。 |
反卷积通俗详细解析与nn.ConvTranspose2d重要参数解释_iioSnail的博客-CSDN博客
卷积的参数量:

3. one by one 卷积
最早出现在NIN文章中,GoogleNet中的Inception得到了使用,作用主要是降维/升维。和普通卷积核的区别就是滤波器大小是1x1,这样每个像素的卷积结果就与其邻域无关,即没有考虑局部信息之间的关系。
既然在空域上相当于对图像整体乘一个因子,那么它是怎么起作用的呢。对图像灰度值的缩放确实没什么收益,收益发生在图像是多通道时。当图像为多通道时,feature map也有相同的数目,这时1x1卷积就相当于不同feature map的线性组合。而根据组合前后的数目相对大小,就可以起到降维升维的作用,实现跨通道的信息整合(相当于一个多层感知机MLP)。
知道了1x1卷积的含义,就可以总结其作用:1.改变维度;2.跨通道信息交互。3.增加非线性
1x1卷积除了以上的优点,还具有计算量小的特点。计算量小不仅仅是因为其尺寸小,更是因为其不会因为计算机“行先序”的特点造成内存访问混乱的问题。虽然卷积很好理解,但是在实际计算中,卷积的感受野在内存中的位置不是连续的,为了解决这个问题,一般使用空间换时间的方法,即使用im2col操作,将特征图和卷积核重新排列,使得卷积操作可以直接使用GEMM矩阵相乘实现。而1x1卷积在Im2col前后的内存存放是相同的。
4. 空洞卷积
Dilated/Atrous Convolution(中文叫做空洞卷积或者膨胀卷积) 或者是 Convolution with holes
| 普通卷积 | 空洞卷积 |
 |  |
空洞卷积首要的作用就是增大感受野。但其实增加感受野的方法至少还有其他两种。一种是VGG中的发现:2个3x3的卷积核的级联相当于5x5的感受野,感受野与层数的关系是(kernel-1)*layer+1,但级联太多就导致网络太深。还有一种是先pooling再卷积,但池化会带来信息的丢失,导致太小的目标信息无法重建。
空洞卷积还有一个特点就是可以保持特征图尺寸不变,这在语义分割中是比较有用的。
dilated conv的问题之一是The Gridding Effect。原因是连续性被跳跃性地取点破坏,感受野是大了,但是对应在第一层上的采样点更加离散了:

图森组通过Hybrid Dilated Convolution (HDC)解决。间隙在空洞卷积中成为膨胀因子(dilated ratio)。HDC的原理简单来说就是几个空洞卷积的膨胀系数使用不同的值,这样空洞的位置就不固定,就能互补,从而减轻格子效应:

Reference:
1.知乎https://www.zhihu.com/question/54149221/answer/323880412
2.空洞卷积(膨胀卷积)的相关知识以及使用建议(HDC原则)-CSDN博客
3. CICC科普
4.线性时不变
5.脉冲响应