一、验证二叉搜索树
题目:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左
子树
只包含 小于 当前节点的数。 - 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
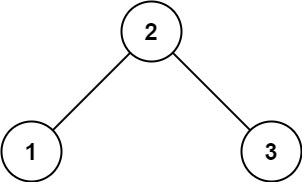
输入:root = [2,1,3] 输出:true
示例 2:
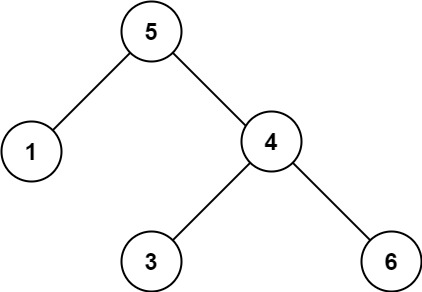
输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
思路:
采用中序:左、中、右的方法,利用双指针,由于二叉搜索树的中序遍历是一个递增的序列,因此只需要比较相邻两个元素的值是否是符合递增的条件即可
代码:
TreeNode pre = null;
public boolean isValidBST(TreeNode root) {
if (root == null)
return true;
// 递归检查左子树
boolean leftValue = isValidBST(root.left);
// 检查当前节点值是否大于前一个节点值
//pre != null表示在第一次遍历时只有一个指针的值被确立,只有在第二次遍历时才能记录两个元素并进行比较,因此第一次if判断不进行
if (pre != null && pre.val >= root.val) {
return false;
}
// 更新 pre 为当前节点
pre = root;
// 递归检查右子树
boolean rightValue = isValidBST(root.right);
// 返回左右子树是否都是 BST
return leftValue && rightValue;
}
-
变量
pre的作用:pre是一个全局变量,用来保存当前节点在中序遍历中的前一个节点。在中序遍历的过程中,通过比较当前节点与前一个节点的值来判断是否满足 BST 的性质(左子树的所有节点值均小于当前节点,右子树的所有节点值均大于当前节点)。
-
isValidBST 方法:
- 方法签名为
boolean isValidBST(TreeNode root),返回一个布尔值,表示以root为根的子树是否是 BST。 - 如果
root为null,则空树被视为 BST,直接返回true。
- 方法签名为
-
递归检查左子树:
boolean leftValue = isValidBST(root.left);递归调用isValidBST方法,检查左子树是否为 BST,并将结果保存在leftValue中。
-
检查当前节点值:
if (pre != null && pre.val >= root.val)检查当前节点root的值与pre的值(前一个节点的值)比较,如果不满足 BST 的性质(即当前节点值小于等于前一个节点的值),则返回false。
-
更新
pre:pre = root;将pre更新为当前节点root,以便在下一次递归中使用。
-
递归检查右子树:
boolean rightValue = isValidBST(root.right);递归调用isValidBST方法,检查右子树是否为 BST,并将结果保存在rightValue中。
-
返回结果:
return leftValue && rightValue;将左子树和右子树是否都为 BST 的结果进行逻辑与操作,最终确定以root为根的子树是否是 BST。
二、 二叉搜索树最小绝对差
题目:
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
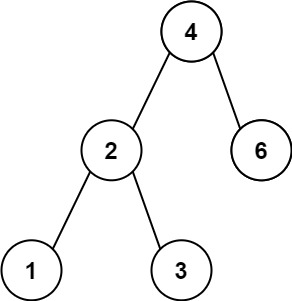
输入:root = [4,2,6,1,3] 输出:1
示例 2:
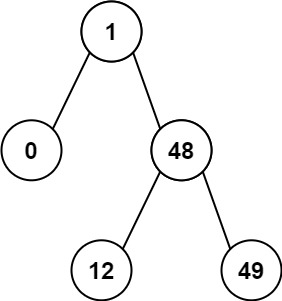
输入:root = [1,0,48,null,null,12,49] 输出:1
思路:
与验证二叉搜索树类似,仍是采用中序遍历的方法,将节点的值按递增排序出来后相邻两值相减,记录最小的绝对差
代码:
int result = Integer.MAX_VALUE; // 初始化结果为整型最大值,用于保存最小差值
TreeNode pre = null; // 用来保存中序遍历中当前节点的前一个节点
/**
* 计算二叉搜索树中任意两个节点值的最小差值
* @param root 当前子树的根节点
* @return 最小差值
*/
public int getMinimumDifference(TreeNode root) {
if (root == null)
return 0; // 如果根节点为空,返回 0,因为空树不存在差值
// 递归处理左子树
getMinimumDifference(root.left);
// 计算当前节点与前一个节点的差值,并更新结果
if (pre != null) {
result = Math.min(result, root.val - pre.val);
}
// 更新前一个节点为当前节点
pre = root;
// 递归处理右子树
getMinimumDifference(root.right);
// 返回最小差值
return result;
}
-
全局变量:
result初始化为整型最大值,用来存储找到的最小节点值差。pre用来跟踪中序遍历中的前一个节点。
-
方法
getMinimumDifference:- 该方法计算给定二叉搜索树中任意两个节点值的最小差值。
root参数表示当前子树的根节点。
-
空节点处理:
- 如果
root为null,表示当前子树为空树,直接返回0,因为空树不存在节点差值。
- 如果
-
递归左子树:
getMinimumDifference(root.left);递归调用,处理左子树。
-
计算节点差值:
if (pre != null) { result = Math.min(result, root.val - pre.val); }- 如果
pre不为null,说明当前节点root不是最左侧节点,计算当前节点值与前一个节点值的差,并更新result为这两者之差的最小值。
- 如果
-
更新前一个节点:
pre = root;更新pre为当前节点root,为下一次递归调用做准备。
-
递归右子树:
getMinimumDifference(root.right);递归处理右子树。
-
返回结果:
return result;返回计算得到的最小差值。
三、 求二叉搜索树中的众数
题目:
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
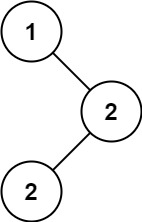
输入:root = [1,null,2,2] 输出:[2]
示例 2:
输入:root = [0] 输出:[0]
思路:
用双指针的方法,在中序遍历得出的递增数组中找出出现频率最大的数,存入结果数组中,如果在遍历的过程中找到出现频率更大的数,则需要将结果数组中存入的数全部清空,同时将频率更高的数加入结果数组,直到遍历完毕
代码:
public void find(TreeNode root) {
if (root == null)
return; // 如果当前节点为空,直接返回
find(root.left); // 递归处理左子树
// 计数逻辑
if (pre == null || root.val != pre.val) {
count = 1; // 如果当前节点与前一个节点不同,重置计数器为1
} else {
count++; // 如果当前节点与前一个节点相同,计数器加1
}
// 更新众数列表和最大计数值
if (count > maxCount) {
resList.clear(); // 如果当前计数大于最大计数,清空之前的结果列表
resList.add(root.val); // 将当前节点值加入结果列表
maxCount = count; // 更新最大计数值
} else if (count == maxCount) {
resList.add(root.val); // 如果当前计数等于最大计数,将当前节点值加入结果列表
}
pre = root; // 更新前一个节点为当前节点
find(root.right); // 递归处理右子树
}
find方法是核心的递归方法,用于执行中序遍历并计算节点值的出现次数。- 如果
root为null,直接返回,结束递归。 - 递归地处理左子树。
- 根据中序遍历的顺序,判断当前节点值与前一个节点值是否相同,更新计数器
count。 - 根据计数器
count的值更新resList中的节点值和maxCount。 - 更新
pre为当前节点,为下一次递归调用做准备。 - 递归地处理右子树。
public int[] findMode(TreeNode root) {
find(root); // 调用递归方法进行中序遍历
int[] res = new int[resList.size()]; // 创建结果数组
for (int i = 0; i < resList.size(); i++) {
res[i] = resList.get(i); // 将结果列表中的值复制到结果数组
}
return res; // 返回结果数组
}
TreeNode pre = null;:用于保存中序遍历中的前一个节点。int maxCount = 0;:记录出现最多次数的节点值的出现次数。int count = 0;:当前节点值的出现次数。ArrayList<Integer> resList = new ArrayList<>();:用于存储找到的所有众数的列表。- 首先调用
find(root)方法来进行中序遍历,并找到众数。 - 创建一个数组
res,将resList中的值复制到res中,并返回。
四、二叉树的最近公共祖先
题目:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
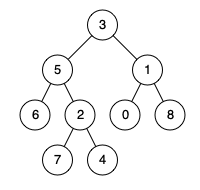
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
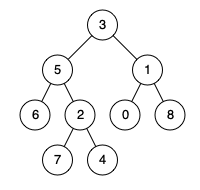
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。 因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1
思路:
采用后序遍历,当左子树和右子树存在p和q时,返回其父节点为最近公共祖先,若左子树没有,右子树存在p和q,返回右子树节点,同理若右子树没有,左子树存在,返回左子树节点
代码:
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 如果当前节点为空,返回null,表示未找到最近公共祖先
if (root == null)
return null;
// 如果当前节点是p或q,说明当前节点就是其中一个目标节点的最近公共祖先
if (root == p || root == q)
return root;
// 递归查找左子树中的最近公共祖先
TreeNode leftValue = lowestCommonAncestor(root.left, p, q);
// 递归查找右子树中的最近公共祖先
TreeNode rightValue = lowestCommonAncestor(root.right, p, q);
// 左右子树分别找到了p和q的最近公共祖先
if (leftValue != null && rightValue != null)
return root; // 当前节点即为最近公共祖先
// 只有右子树找到了最近公共祖先
if (leftValue == null && rightValue != null) {
return rightValue;
} else if (leftValue != null && rightValue == null) { // 只有左子树找到了最近公共祖先
return leftValue;
} else {
return null; // 左右子树均未找到最近公共祖先
}
}
- 如果当前节点
root为空,直接返回null,表示未找到最近公共祖先。 - 如果当前节点
root等于p或者q,说明当前节点就是其中一个目标节点,直接返回当前节点root。 - 如果左子树找到了
p和q的最近公共祖先leftValue,右子树也找到了p和q的最近公共祖先rightValue,那么当前节点root就是它们的最近公共祖先,直接返回root。 - 如果只有左子树找到了最近公共祖先
leftValue,则返回leftValue。 - 如果只有右子树找到了最近公共祖先
rightValue,则返回rightValue。 - 如果左右子树都没有找到,则返回
null,表示在当前子树中不存在p和q的最近公共祖先。
五、二叉搜索树的最近公共祖先
题目:
给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
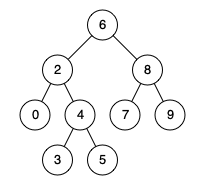
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2和节点 4的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
思路:
利用二叉搜索树的性质,如果p和q的值小于根节点的值,则说明其最近公共祖先在左子树中,反之如果p和q的值大于根节点的值,则说明其最近公共祖先在右子树中,在遍历过程中如果节点的值大于p且小于p,说明该节点为最近公共祖先
代码:
//递归法
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return null;
// 如果当前节点的值大于p和q的值,则它们的最近公共祖先一定在左子树中
if (root.val > p.val && root.val > q.val) {
TreeNode left = lowestCommonAncestor(root.left, p, q);
if (left != null) {
return left; // 如果左子树递归找到了最近公共祖先,直接返回
}
}
// 如果当前节点的值小于p和q的值,则它们的最近公共祖先一定在右子树中
else if (root.val < p.val && root.val < q.val) {
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (right != null) {
return right; // 如果右子树递归找到了最近公共祖先,直接返回
}
}
// 如果当前节点的值介于p和q的值之间,或者当前节点就是p或q,则当前节点就是最近公共祖先
return root;
}
- 如果当前节点的值大于
p和q的值,则说明p和q都在当前节点的左子树中,递归地在左子树中查找最近公共祖先。 - 如果当前节点的值小于
p和q的值,则说明p和q都在当前节点的右子树中,递归地在右子树中查找最近公共祖先。
//迭代法
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 迭代查找最近公共祖先
while (root != null) {
if (root.val < p.val && root.val < q.val) {
// 如果根节点的值都小于p和q的值,说明p和q都在右子树
root = root.right; // 移动到右子树继续查找
} else if (root.val > p.val && root.val > q.val) {
// 如果根节点的值都大于p和q的值,说明p和q都在左子树
root = root.left; // 移动到左子树继续查找
} else {
// 如果根节点的值介于p和q的值之间,或者根节点就是p或q,返回根节点
return root; // 找到最近公共祖先,返回
}
}
// 如果未找到最近公共祖先,返回null
return null;
}
- 利用
while循环,只要当前节点root不为空,就进行迭代处理。 - 在每一轮迭代中,根据
root的值和p, q的值的关系来决定向左子树或右子树移动:- 如果
root.val小于p.val和q.val,说明p和q都在root的右子树中,因此将root移动到右子树root.right。 - 如果
root.val大于p.val和q.val,说明p和q都在root的左子树中,因此将root移动到左子树root.left。 - 如果
root.val介于p.val和q.val之间,或者等于其中之一的值,说明root就是p和q的最近公共祖先,直接返回root。
- 如果
今天的学习就到这里