二维数组前缀和(Leetcode304)
想法(参考题解):
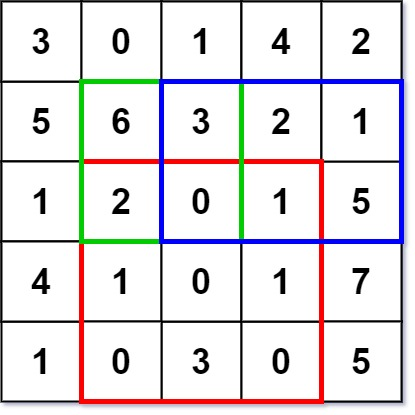
如上图,在矩阵中根据给定的方框围成的范围,确定范围内元素之和。题目:二维区域和检索 - 矩阵不可变。思路就是使用前缀和,前缀和表示的是面积,每一个位置对应的前缀和都表示以当前坐标为右下角所计算的“面积”中的前缀和,也就是当前面积覆盖所有区域的累加和。然后通过对面积的相加减,就可以计算得出下一个位置的累加和。以此类推;
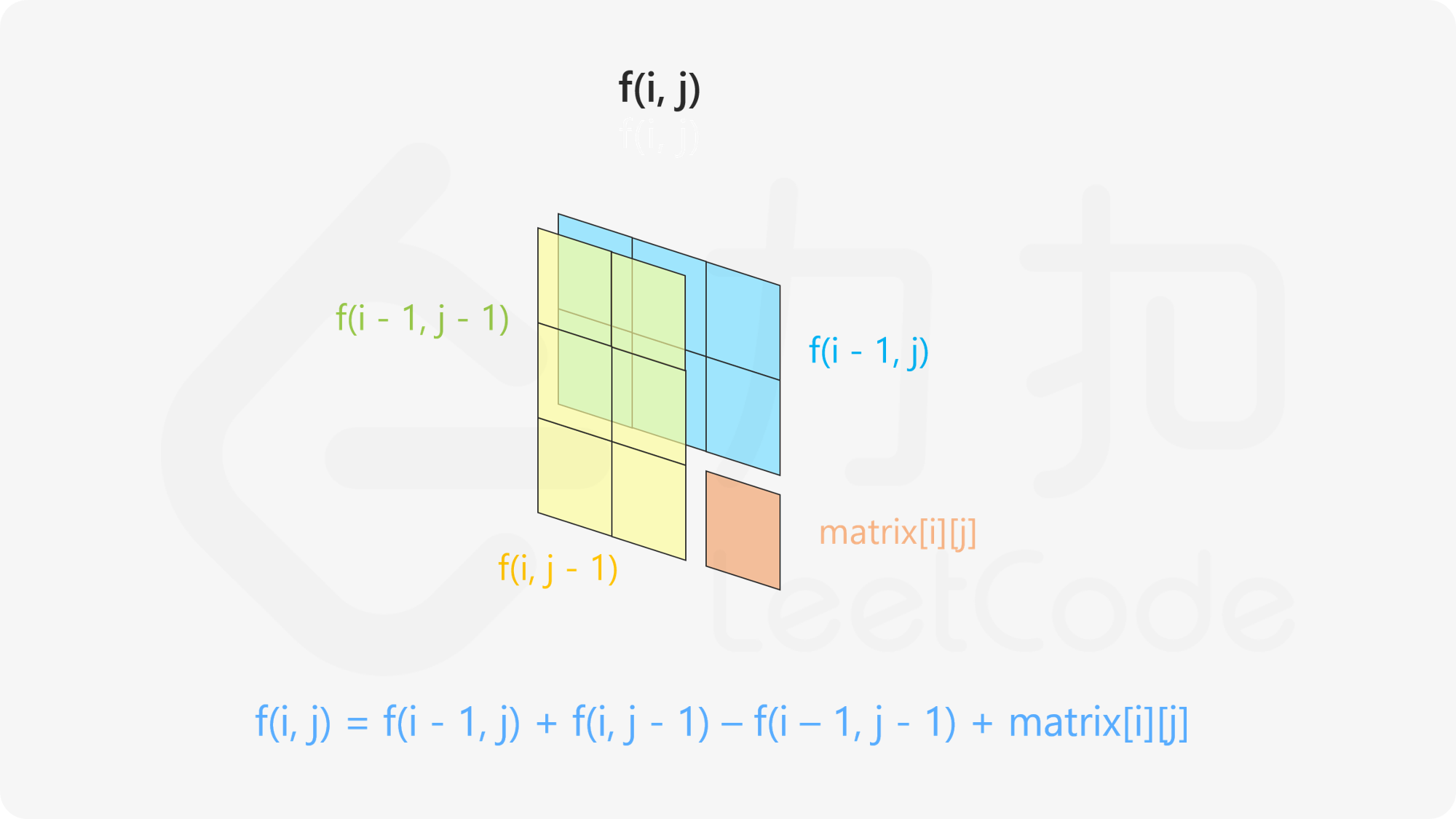

解题过程:
在初始化过程中创建一个前缀和数组,前缀和数组的长度和宽度都比原数组大1,然后计算当前[i,j]位置的前缀和的时候,使用一种前缀面积的方式去获取前缀前缀和数组的面积计算f(i, j)=f(i - 1, j) + f(i, j - 1) - f(i - 1, j - 1) +arr[i][j] 得到前缀和数组之后,在传入参数的时候左上角和右下角相应的+1因为前缀和数组从(1, 1)开始有意义值,然后同样通过面积相减的方式来得到所取范围的f(r1, c1, r2, c2) = f(r2, c2) - f(r1 - 1, c2) - f(r2, c1 - 1) + f(r1 - 1, c1 - 1)
code:
class NumMatrix {
private:
vector<vector<int>> _vec;
public:
NumMatrix(vector<vector<int>>& matrix) {
int n = matrix.size(), m = n == 0 ? 0 : matrix[0].size();
_vec.resize(n + 1, vector<int>(m + 1, 0));
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= m; ++j)
{
_vec[i][j] = _vec[i][j - 1] + _vec[i - 1][j] - \
_vec[i -1][j - 1] + matrix[i - 1][j - 1];
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
row1++; row2++; col1++; col2++;
return _vec[row2][col2] - _vec[row1 - 1][col2] - \
_vec[row2][col1 - 1] + _vec[row1 - 1][col1 - 1];
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/

















