上一篇文章我们学习了基本的概率论内容-排列组合,本次我们学习概率论公理的内容,正式开始计算概率,在开始前我们需要学习一些基本概念。
目录
一.样本空间和事件
1.样本空间
2.事件
3.交并补
二、概率公理
1.基本公理
2.对称差
2.布尔不等式
三、具有等可能结果的样本空间
四、连续集函数
一.样本空间和事件
1.样本空间
一个试验的所有可能结果构成的集合,称为试验的样本空间(Sample Space),记作S。如扔两枚硬币,样本空间为:
如仍两个骰子,考察点数,那么样本空间为:
2.事件
样本空间的任意子集是事件(event),如果实验的结果包含在事件内,那么就是事件发生了
3.交并补
这个过于简单,画个Venn图结束:分别是并集(或)、交集(且)、补集、包含

基本运算遵循代数运算:

这里需要学习一个进行运算的德摩根率,证明过程不论述:


二、概率公理
1.基本公理
如果事件E中的样本点数量为n(E),而样本空间Ω中的样本点数量为n(Ω),假设样本空间Ω中的每个样本点发生的可能性相等,那么事件E发生的概率由下式给出:

我们得到几条公理:
(1)
(2)
(3)
(4)
2.对称差
对称差包含了属于E或F但不同时属于两者的所有元素。换句话说,对称差包含了那些仅属于E或仅属于F的元素,但不包括同时属于E和F的元素。
![]()
E Δ F = (E ∪ F) - (E ∩ F)
(1)交换律:E Δ F = F Δ E
(2)结合律:(E Δ F) Δ G = E Δ (F Δ G)
(3)对称差与并集的关系:E Δ (F ∪ G) = (E Δ F) ∩ (E Δ G)
(4)对称差与交集的关系:E Δ (F ∩ G) = (E Δ F) ∪ (E Δ G)
我们使用Mathematica可视化:

2.布尔不等式
布尔不等式指出对于全部事件的概率不大于单个事件的概率总和(字面意思理解):

我们通过一个例题加深我们的理解:
例1:从集合{1,...,1000}中随机有放回地抽取整数。设事件E为抽到的数能同时被5、7或13整除。用Di表示抽到的数能被i整除的事件,取到一个这样的数的概率是多少?

我们使用mathematica进行计算:

似乎有点复杂,我们使用Java写一个简单模拟程序:
import java.util.Random;
public class Simulation {
public static void main(String[] args) {
int totalNumbers = 1000;
int simulations = 3000;
int count = 0;
Random random = new Random();
for (int i = 0; i < simulations; i++) {
int number = random.nextInt(totalNumbers) + 1; // 生成1到1000之间的随机数
if (number % 5 == 0 || number % 7 == 0 || number % 13 == 0) {
count++;
}
}
double simulatedProbability = (double) count / simulations;
System.out.println("通过模拟得到的概率是: " + simulatedProbability);
}
}![]()
三、具有等可能结果的样本空间
我们通过一些例题来学习概率的基本计算
例1:从一副充分洗好的52张标准扑克牌中随机抽取一张牌,求这张牌同时是红心和A的概率

我们可以使用德摩根率反过来看这个问题:
![]()
非红心牌有多少张?有39张。在这39张非红心中,有3张是A。所以有36张既不是红心也不是A

例2:5个球随机扔进10个箱子,求没有箱子内多于一个球的概率
![]()


两种思路均可以,一种是考虑全局,一种是每次进行一次考虑
例3:有15个新生,12个男生,3个女生,随机分到三个教室求(1)每个班一个女生的概率(2)一个班三个女生的概率
这个用到前一篇的分组问题计算,忘记的朋友可以回顾一下:【基于Mathematica的最易懂概率论】-1-排列组合-CSDN博客
(1)我们先对样本空间计数:

接下来思考事件计数,三个女生分别去三个班就是3的全排列,剩下四个位置是男生分组排列

因此概率计算为:

(2)三个女生要在一个班,因此男生的分组为5、5、2,而女生所在班有三种可能性


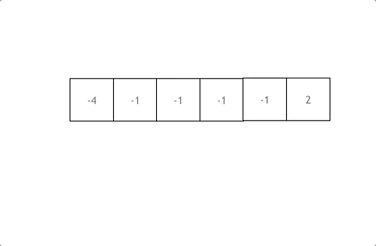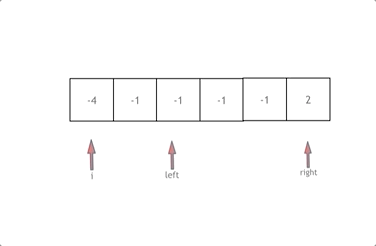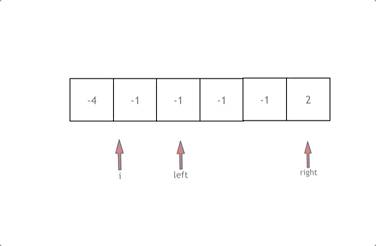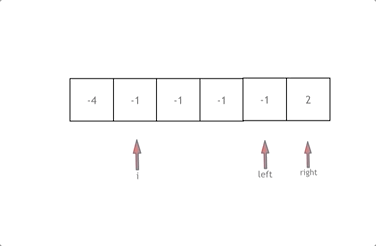
例4:我们考虑一个复杂的占位问题:一个球队分别在一个赛季的输赢可以表示为:WLWLWLWWWLLWWWWWWWLL这样的输赢序列,其中赢了13场,输赢认为是随机的,我们想知道连赢5场的概率是多少?
我们用x表示这一对连赢的队列,那么:
用y表示另一对连赢的队列,那么:
因此这就转变为两个占位问题:

令y1=z1-1,y6=z6-1,系数变换后得到:
![]()
因此得到:

四、连续集函数
如果事件序列En满足:
![]()
那么就是递增序列,如果事件序列En满足:
![]()
那么就是递减序列
我们学习波莱尔-坎泰利引理:如果有无穷个概率事件,它们发生的概率之和是有限的,那么其中的无限多个事件一同发生的概率是零。


例:考虑一个公平的硬币独立抛掷的序列。每当出现r个连续正面时,我们称之为一次成功。如果我们无限次地抛掷硬币,成功的概率为1嘛?
每当一次成功发生时,我们认为一个实验已经发生。设An为已经发生了n次实验的事件

我们看到An是一个单调序列。根据概率的连续性,我们可以得出结论:

因此: