题目描述

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获 所有 被围绕的区域：

• 连接：一个单元格与水平或垂直方向上相邻的单元格连接。
• 区域：连接所有 'O' 的单元格来形成一个区域。
• 围绕：如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过将输入矩阵 board 中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]

输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]

解释：

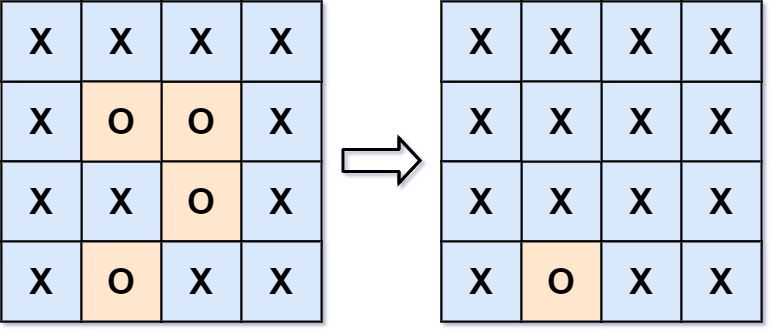
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

题目解析

题目中的意思就是指将数组中被”X“包围”O“全部变成”X“，而只有和边界”O“相连的”O“才不会被”X“包围。

因此我们就可以从整个图的边界开始查找，找到所有与边界”O“相连的”X“，除了这些”O“，把剩下的全部”O“都变成”X“。

我们可以使用一个数组flag来标记各个位置，flase表示会此处为”X“或是可以被替换成”X“，true表示此处为和边界相连的”O“。

在搜索时可以使用深度优先搜索，从边界搜索到图中所有的符号，最后根据标记所得将所有的标记为false的变为”X“，这样我们就成功替换了所有被包围的”O“。

代码实现

class Solution {
    public void solve(char[][] board) {
        int n = board.length;
        int m = board[0].length;
        boolean[][] flag = new boolean[n][m];
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                flag[i][j] = false;
            }
        }
        for(int i=0;i<m;i++){
            if(board[0][i]=='O'&& !flag[0][i]){
                dfs(board,flag,0,i);
            }
            if(board[n-1][i]=='O'&& !flag[n-1][i]){
                dfs(board,flag,n-1,i);
            }
            
        }
        for(int i=0;i<n;i++){
            if(board[i][0]=='O'&& !flag[i][0] ){
                dfs(board,flag,i,0);
            }
            if(board[i][m-1]=='O'&& !flag[i][m-1]){
                dfs(board,flag,i,m-1);
            }
        }
        
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
               if(flag[i][j] == false){
                   board[i][j] = 'X';
               }
            }
        }
    }
    public void dfs(char[][] board,boolean[][] flag,int x,int y){
        if(x<0||x>=board.length||y<0||y>=board[0].length||board[x][y]=='X'||flag[x][y]){
            return;
        }
        flag[x][y] = true;
        dfs(board,flag,x,y-1);
        dfs(board,flag,x+1,y);
        dfs(board,flag,x-1,y);
        dfs(board,flag,x,y+1);
    }
}