这是C++算法基础-基础算法专栏的第十三篇文章，专栏详情请见此处。

---

引入

        上次我们学习了前缀和的实现，它可以快速解决求区间和问题。这次我们要学习差分，它是前缀和的逆运算，可以快速解决对序列的一个区间同时加或减一个数这样的问题。

        对序列的一个区间加或减一个数，它的朴素做法时间复杂度为 ，而用差分做法就可以将时间复杂度优化为。

        下面我们就来讲一维差分的实现。

定义

        差分是一种和前缀和相对的策略，可以当做是求和的逆运算。

过程

        表示

        对于原数组，我们尝试构造一个数组，使得数组为数组的前缀和数组，即，也就是说，，这时，我们就把数组称为数组的差分数组。

        赋值

        那如何构造这个数组呢？

        我们令且。可以看出，数组每一位的值是数组中两个相邻元素的差值。于是，我们在输入数组时同时进行对的赋值。

        处理区间值

        当我们想将数组区间中的数值都加，应该怎么去做呢？这里我们用图表加以理解，表示当前位未计算，表示当前位已计算。

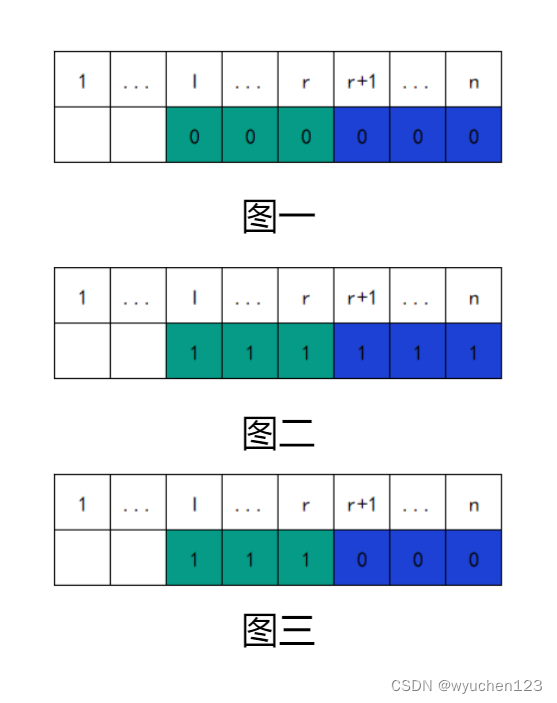
        首先，图一展示了起始状态，然后，我们将计入总和（图二），也就是将内的数值都加，但我们并不需要之后的数计入总和，所以最后将减去（图三）。

        得出结论： 将数组区间中的数值都加：，。

        代码

        下面给出一维差分代码：

表示：a[i]=b[1]+b[2]+...+b[i]
赋值：b[i]=a[i]-a[i-1]
处理：b[l]+=c,b[r+1]-=c

---

上一篇-二维前缀和的实现    C++算法基础专栏文章    下一篇-二维差分的实现

---

每周六更新一篇文章，内容一般是自己总结的经验或是在其他网站上整理的优质内容

点个赞，关注一下呗~