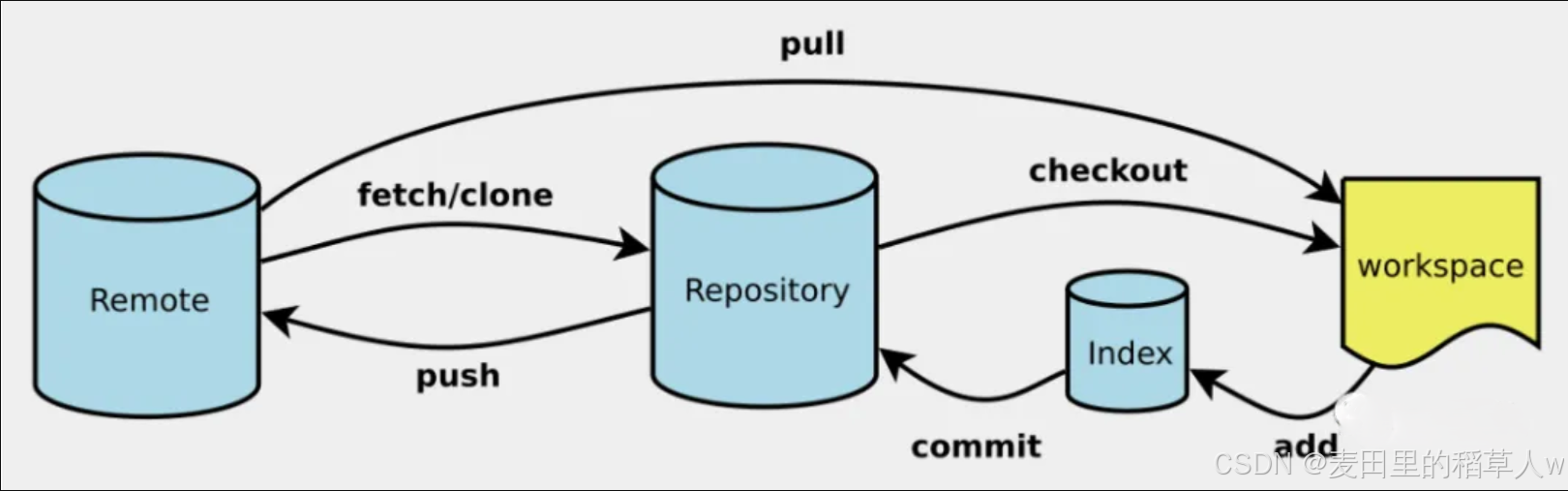
好的,我们开始吧。首先第一个问题,神经网络的本质是什么?是古典主义的人类的神经元吗?绝对不是,他只是一个优化函数
y
=
f
θ
(
x
)
y = f_{\theta}(x)
y=fθ(x)
这和小学学到的线性函数拟合并无本质区别。只是其中参数
θ
\theta
θ是大量的参数,并且函数
f
θ
f_{\theta}
fθ本身的形式也会非常复杂。相应的参数
θ
\theta
θ也无法像线性拟合一样,直接列方程求解,而是依赖于优化算法。
所以今天,我们就尝试用神经网络,去学习几个函数表达式。
训练代码解读
不多说了直接贴代码
import numpy as np
import math
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
class Net(nn.Module):
def __init__(self, num_layers, input_size, hidden_size, output_size):
super(Net, self).__init__()
self.layers = nn.ModuleList([nn.Linear(input_size, hidden_size, bias=True)] +
[nn.Linear(hidden_size, hidden_size, bias=True) for _ in range(num_layers - 2)] +
[nn.Linear(hidden_size, output_size, bias=True)])
def forward(self, x):
for layer in self.layers:
x = nn.functional.gelu(layer(x))
return x
if __name__=="__main__":
# 被训练函数---------------------------
x = np.linspace(0.1, 2.1, 100)
y = [[math.exp(ele)*ele, math.exp(ele), ele*ele] for ele in x]
plt.plot(x, y)
plt.show()
# 训练部分------------------------
# 生成被训练数据------------------------
x = torch.Tensor(x.reshape(-1,1))
y = torch.Tensor(y)
# 初始化网络
net = Net(6, 1, 32, 3)
# 定义损失函数和优化器
loss_fn = nn.MSELoss(reduction='sum')
optimizer = optim.Adam(net.parameters(), lr=0.01)
# 训练模型
epochs = 1000
for epoch in range(epochs):
y_pred = net(x)
loss = loss_fn(y_pred, y)
optimizer.zero_grad() #梯度清零,否则梯度会累积
loss.backward() #计算参数关于loss函数的梯度,需要做梯度会穿
optimizer.step() #利用梯度对model参数进行一次训练
if epoch % 10 == 0:
print('epoch: ', epoch, " loss: ", loss.item())
if epoch % 100 == 0:
plt.clf()
plt.plot(x, y,'b-',x, y_pred.detach().numpy(),'r-')
plt.show()
这里多说一句撒,关于训练的写法,我觉得mindspore设计得是比pytorch要好的。optimizer.zero_grad()这种事情,mindspore就不需要做,不如说正常人前一次梯度都不会保留吧,默认不保留才是合理的吧。第二个是,获取梯度的grad,loss.backward应该显式的写出来,然后传进优化器的一次训练步才更加符合直觉,比如像下面这样
grad = loss.backward() #梯度回传获取grad
optimizer.step(grad) #利用梯度对net的参数进行一次训练
# 上述两行纯属个人yy,不能运行的哈
训练结果如下



可以看到300左右就已经收敛得比较好了。
神经网络的局限性与正则化的重要性
简单粗暴的将被学习的函数第一个分量减去10
x = np.linspace(0.1, 2.1, 100)
y = [[math.exp(ele)*ele - 10, math.exp(ele), ele*ele] for ele in x]
突然就不能学了

这其实是因为,我们使用的激活函数,为gelu函数。嗯差不多长下面这样,这种激活函数是没法表示负值的。导致整个神经网络没法表示负数。

所以说神经网络也不完全是魔法,而是一个优化问题。我们需要先找到能以较少参数就表示被优化函数的网络,然后再对这个网络里面的参数进行优化,才能得到合理的结果。对当前情况,我们选一个,能表示较大负数的激活函数,例如:呃?!我震惊的发现好像没有类似这样的激活函数,AI训练的问题大多数都是非负的。
好吧,所以神经网络要学习的问题,我们一定要做合适的正则化或者归一化,让我们的网络能够表示当前的问题才行。