题干描述
一个公司在全国有 n 个分部,它们之间有的有道路连接。一开始,所有分部通过这些道路两两之间互相可以到达。
公司意识到在分部之间旅行花费了太多时间,所以它们决定关闭一些分部(也可能不关闭任何分部),同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。
两个分部之间的 距离 是通过道路长度之和的 最小值 。
给你整数 n ,maxDistance 和下标从 0 开始的二维整数数组 roads ,其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的 无向 道路。
请你返回关闭分部的可行方案数目,满足每个方案里剩余分部之间的最远距离不超过 maxDistance。
注意,关闭一个分部后,与之相连的所有道路不可通行。
注意,两个分部之间可能会有多条道路。
示例 1:
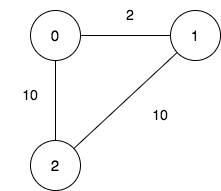
输入:n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]] 输出:5 解释:可行的关闭分部方案有: - 关闭分部集合 [2] ,剩余分部为 [0,1] ,它们之间的距离为 2 。 - 关闭分部集合 [0,1] ,剩余分部为 [2] 。 - 关闭分部集合 [1,2] ,剩余分部为 [0] 。 - 关闭分部集合 [0,2] ,剩余分部为 [1] 。 - 关闭分部集合 [0,1,2] ,关闭后没有剩余分部。 总共有 5 种可行的关闭方案。
示例 2:
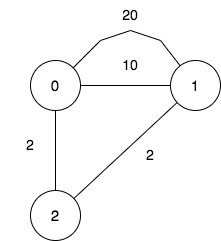
输入:n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]] 输出:7 解释:可行的关闭分部方案有: - 关闭分部集合 [] ,剩余分部为 [0,1,2] ,它们之间的最远距离为 4 。 - 关闭分部集合 [0] ,剩余分部为 [1,2] ,它们之间的距离为 2 。 - 关闭分部集合 [1] ,剩余分部为 [0,2] ,它们之间的距离为 2 。 - 关闭分部集合 [0,1] ,剩余分部为 [2] 。 - 关闭分部集合 [1,2] ,剩余分部为 [0] 。 - 关闭分部集合 [0,2] ,剩余分部为 [1] 。 - 关闭分部集合 [0,1,2] ,关闭后没有剩余分部。 总共有 7 种可行的关闭方案。
示例 3:
输入:n = 1, maxDistance = 10, roads = [] 输出:2 解释:可行的关闭分部方案有: - 关闭分部集合 [] ,剩余分部为 [0] 。 - 关闭分部集合 [0] ,关闭后没有剩余分部。 总共有 2 种可行的关闭方案。
题干分析
问题描述
- 给定一个由n个分部组成的图,每个分部之间有若干条道路。
- 我们需要计算可以关闭分部的方案数量,满足剩余分部之间的最远距离不超过maxDistance。
解题方法
- 使用位掩码枚举所有可能的分部组合。
- 对每个组合,使用Floyd-Warshall算法计算所有节点对之间的最短路径。
- 验证每个组合是否满足条件:所有节点两两之间的最远距离不超过maxDistance。
代码设计
1.初始化和输入解析
- 动态分配opened数组,用于表示哪些分部是打开的。
- 动态分配二维数组d,用于存储节点之间的最短距离。
int res = 0;
int* opened = (int*)malloc(n * sizeof(int));//动态分配数组opened,用于表示那些分部是打开的
int** d = (int**)malloc(n * sizeof(int*));//动态分配二维数组d,用于存储节点之间的最短距离
for (int i = 0; i < n; i++)
{
d[i] = (int*)malloc(n * sizeof(int));
}2.枚举所有可能的子集组合
- 使用掩码mask枚举所有可能的子集组合,每个掩码表示一种组合方式。
//枚举所有可能的子集组合,使用掩码表示
for (int mask = 0; mask < (1 << n); mask++)
{
//初始化opened数组,表示当前子集中那些节点是打开的
for (int i = 0; i < n; i++)
{
opened[i] = mask & (1 << i);
}
//初始化距离矩阵d,将所有的节点对之间的距离初始化为一个很大的值(表示无穷大)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) {
d[i][j] = 1000000;
}
}3.更新距离矩阵
- 根据当前子集中打开的节点,更新距离矩阵d。
- 仅当两个节点都在当前子集中时,才更新这两个节点之间的距离。
//根据当前子集中的打开节点更新距离矩阵d
for (int k = 0; k < roadsSize; k++)
{
int i = roads[k][0], j = roads[k][1], r = roads[k][2];
if (opened[i] && opened[j]) {
d[i][j] = d[j][i] == (d[i][j] < r) ? d[i][j] : r;
}
}4. Floyd-Warshall 算法
- 使用Floyd-Warshall 算法计算当前子集中所有节点对之间的最短距离。
- 如果两个节点之间存在间接路径,更新它们之间的最短路径。
//使用Floyd-Warshall 算法计算所有节点对之间的最短路径
for (int k = 0; k < n; k++)
{
if (opened[k]) {
for (int i = 0; i < n; i++)
{
if (opened[i]) {
for (int j = 0; j < n; j++)
{
if (opened[j]) {
if (d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
}
}
}
}5.验证子集
- 检查当前子集中所有节点两两之间的最远距离是否不超过maxDistance。
- 如果所有节点都满足条件,则将当前子集计入结果res。
//验证当前子集是否满足所有节点两两之间的最远距离不超过maxDistance
int good = 1;
for (int i = 0; i < n; i++)
{
if (opened[i]) {
for (int j = i + 1; j < n; j++)
{
if (opened[j] && d[i][j] > maxDistance) {
good = 0;
break;
}
}
if (!good)
{
break;
}
}
res += good;
}6.释放动态内存
- 释放之前动态分配的内存避免内存泄漏。
//释放动态分配的内存
for (int i = 0; i < n; i++)
{
free(d[i]);
}
free(d);
free(opened);
return res;完整的代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
int numberOfSets(int n, int maxDistance, int** roads, int roadsSize, int* roadsColSize) {
int res = 0;
int* opened = (int*)malloc(n * sizeof(int));//动态分配数组opened,用于表示那些分部是打开的
int** d = (int**)malloc(n * sizeof(int*));//动态分配二维数组d,用于存储节点之间的最短距离
for (int i = 0; i < n; i++)
{
d[i] = (int*)malloc(n * sizeof(int));
}
//枚举所有可能的子集组合,使用掩码表示
for (int mask = 0; mask < (1 << n); mask++)
{
//初始化opened数组,表示当前子集中那些节点是打开的
for (int i = 0; i < n; i++)
{
opened[i] = mask & (1 << i);
}
//初始化距离矩阵d,将所有的节点对之间的距离初始化为一个很大的值(表示无穷大)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) {
d[i][j] = 1000000;
}
}
//根据当前子集中的打开节点更新距离矩阵d
for (int k = 0; k < roadsSize; k++)
{
int i = roads[k][0], j = roads[k][1], r = roads[k][2];
if (opened[i] && opened[j]) {
d[i][j] = d[j][i] == (d[i][j] < r) ? d[i][j] : r;
}
}
//使用Floyd-Warshall 算法计算所有节点对之间的最短路径
for (int k = 0; k < n; k++)
{
if (opened[k]) {
for (int i = 0; i < n; i++)
{
if (opened[i]) {
for (int j = 0; j < n; j++)
{
if (opened[j]) {
if (d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
}
}
}
}
//验证当前子集是否满足所有节点两两之间的最远距离不超过maxDistance
int good = 1;
for (int i = 0; i < n; i++)
{
if (opened[i]) {
for (int j = i + 1; j < n; j++)
{
if (opened[j] && d[i][j] > maxDistance) {
good = 0;
break;
}
}
if (!good)
{
break;
}
}
res += good;
}
//释放动态分配的内存
for (int i = 0; i < n; i++)
{
free(d[i]);
}
free(d);
free(opened);
return res;
}
int main() {
int n = 3;
int maxDistance = 5;
int roadsSize = 3;
int roadsColSize[] = { 3, 3, 3 };
// 动态分配二维数组 roads,用于存储道路信息
int** roads = (int**)malloc(roadsSize * sizeof(int*));
for (int i = 0; i < roadsSize; i++) {
roads[i] = (int*)malloc(3 * sizeof(int));
}
// 初始化道路信息
roads[0][0] = 0; roads[0][1] = 1; roads[0][2] = 2;
roads[1][0] = 1; roads[1][1] = 2; roads[1][2] = 10;
roads[2][0] = 0; roads[2][1] = 2; roads[2][2] = 10;
// 计算并输出结果
int result = numberOfSets(n, maxDistance, roads, roadsSize, roadsColSize);
printf("Total feasible solutions: %d\n", result);
// 释放动态分配的内存
for (int i = 0; i < roadsSize; i++) {
free(roads[i]);
}
free(roads);
return 0;
}