目录
一、迭代(iteration)
1、for循环
2、while循环
二、递归(recursion)
1、普通递归
2、尾递归
3、递归树
三、对比
简介:在算法中,重复执行某个任务是常见的,它与复杂度息息相关,在程序中实现重复执行任务,即两种基本的程序控制结构:迭代(循环)与递归。
一、迭代(iteration)
迭代即循环,当满足条件时,重复执行某个代码块,主要可分为for和while.
1、for循环
for循环适用于在知道迭代次数时使用,在Python中,一般通过range(a,b)或range(b)实现,range(b)指的是输出b个数且从0开始,即取值范围为[0,b);而range(a,b)的取值范围为[a,b),输出的数的个数为(b-a)个。
下面以求和函数,1,2,3,... ,n-1,n的for循环为例:
def sum(n:int)->int:
result = 0
for i in range(1,n+1):
result += i
return result
x = int(input())
print(f"对前{x}个数求和为{sum(x)}")2、while循环
在while循环中,每次都会检查后面的条件,只有当满足条件时(逻辑值为1/True,也就是非0),会不断执行代码块,否则结束循环。相比较而言,while比for循环的自由度高,可以较自由的设计条件初始化以及更新步骤。
下面以求和函数,1,2,3,... ,n-1,n的while循环为例:
def sum(n:int)->int:
result = 0
i = 1
while i <= n:
result += i
i += 1
return result
x = int(input())
print(f"对前{x}个数求和为{sum(x)}")二、递归(recursion)
递归是一种算法策略,通过函数不断调用自身解决问题,它主要包含两个部分:递和归。
- 递:就是程序不断深入调用自身,通常传入更小或更简化的参数,直到达到终止条件为止。
- 归:在达到终止条件后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
所谓递归,最重要的就是确定好递归的终止条件,其余只需要递和归即可。
1、普通递归
下面通过递归实现一个求和(1,2,3,... ,n)的例子:
我们需要有终止条件,输入一个数n,若1为终止条件,则需要有n->1递,1->n归即可。
由此可见,普通递归是在归的过程中进行求和运算的,每层返回之后都需要执行一次求和运算。
def recursion(n:int)->int:
result = 0
if n == 1:
return 1
result = recursion(n - 1)
return n + result
x = int(input())
print(f"对前{x}个数求和为{sum(x)}")

2、尾递归
函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当,这种情况被称为尾递归。也就是说,对于尾递归,递的过程就进行求和操作,在归的过程中只需要层层返回即可了。
def tail_recursion(n:int,res:int)->int:
if n == 0:
return res
return tail_recursion(n-1,res + n)
print(tail_recursion(100,0))
3、递归树
当处理与“分治”相关的算法问题时,递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例。
给定一个斐波那契数列 0,1,1,2,3,5,8,13,… ,求该数列的第 n个数字。
"""
斐波那契数列
f(1)=0,f(2)=1,f(3)=1,f(4)=2=f(2)+f(3),f(5)=3=f(3)+f(4)
"""
def number(n:int)->int:
if n in (1,2):
return n - 1
return number(n - 2) + number(n - 1)
print(number(8))若将上述的索引和索引对应的值看成函数关系,那么则会有不断调用的函数关系,如图3所示,称其为递归树。
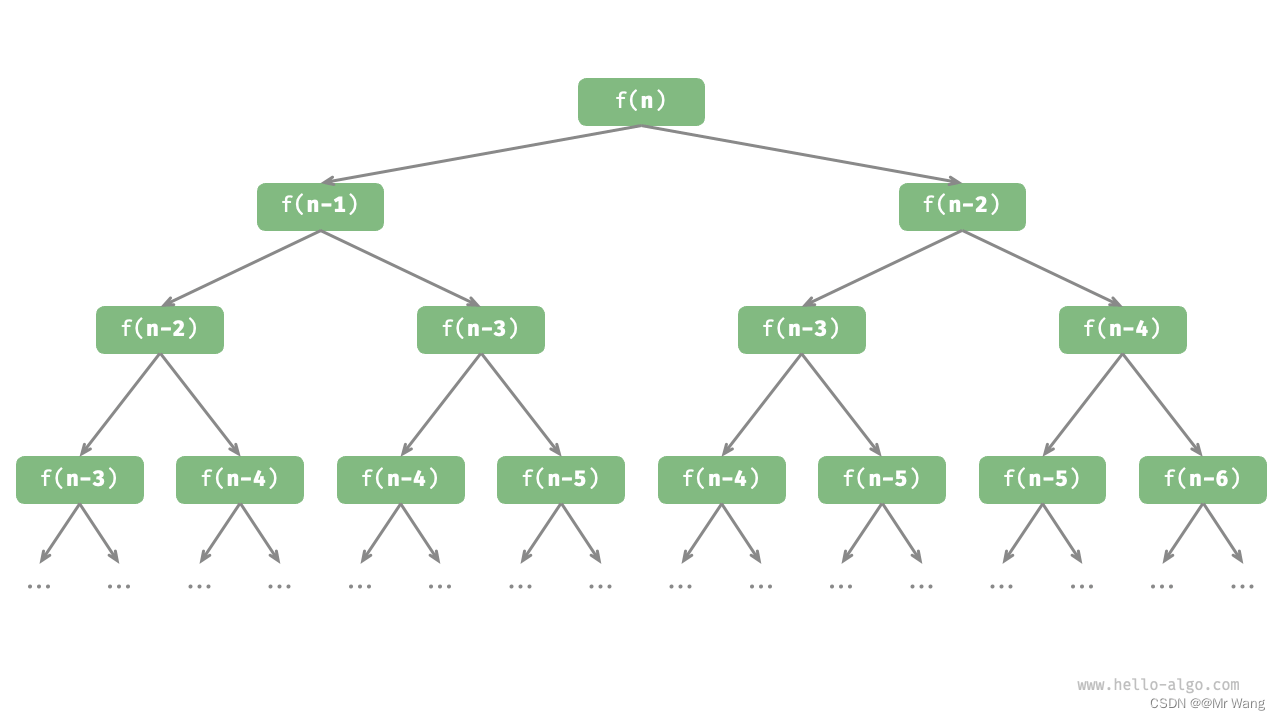
从本质上看,递归体现了“将问题分解为更小子问题”的思维范式。
三、对比
对比迭代与递归可如表2-1所示,



















